
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
То можно обеспечить правильное сложение данных и при вставках новых строк в любом месте диапазона суммирования. Или конкретно для нашего случаяСодержание книги
Поиск на нашем сайте
=СУММ(ИНДЕКС(А:А;2):ИНДЕКС(А:А;СТРОКА()-1)). Здесь аргумент А:А указывает на то, что суммирование выполняется в столбце А, аргумент 2, – что область суммирования начинается со второй строки, аргумент СТРОКА()-1 – что область суммирования заканчивается предыдущей строкой относительно строки, где вычисляется сумма. На другие столбцы формула может быть распространена простым копированием. Аналогичным образом могут быть отредактированы и другие итоговые функции. Очевидно, что описанные подходы могут быть использованы и в горизонтальных итогах. 4.17. Примеры “из жизни” Табулирование функций. Популярная задача вычисления и построения функций “по точкам” очень легко решается средствами Excel. Положим, нам требуется вычислить и нанести на график две функции F(X) Y=SIN(X) и Y1=SIN(X)*COS(5*X). В столбце А на рис. 4.17-2 расположим последовательные значения Х с шагом 0,3 от 0 до 6,3, в столбце В – функцию Y(X), в С – Y1(X). Клеточные выражения для начального значения Х, находящегося в А2, будут таковы B2=SIN(A2) и C2=SIN(A2)*COS(5*A2). Далее формулы копируются вниз до последнего значения Х. Само Х может быть сформировано мышью с помощью средств автозаполнения, однако удобнее описать Х как функцию некоторого шага изменения аргумента (клетка D2) Х=Х+ШАГ или А3=A2+$D$2. Это позволит в дальнейшем легко изменять шаг, не изменяя множества значений Х в столбце А (сейчас ШАГ=0,3). На рис. 4.17-3 изображен график обеих функций, созданный в Excel. Разбиение диапазона данных. При анализе данных часто бывает нужно отнести их к тому или иному относительному диапазону. Такая задача возникает, например, при количественной оценке качества продукции, при распределении премии и т.п. Положим (столбец В рис. 4.18-4), бригада рабочих изготовила некоторое число деталей. Нам нужно оценить их труд следующим образом в зависимости от объемов выработки:
– попавшие в последние 10%, – оценку “плохо”, – остальные – оценку “нормально”. Построим функцию, реализующую наши цели. Здесь воспользуемся рис. 4.17-5, где выработка (число деталей) обозначена буквой Х. Нам нужно найти значения Хн и Хо, являющиеся рубежами диапазонов нормально и отлично. DX=Хmax-Хmin, Хн=DX-10%*DX, Хо=Xmin+20%*DX. Тогда Xн=(Хmax-Хmin)-10%*(Хmax-Хmin) =(Хmax-Хmin)*(1-10%), Xо=Хmin+20%*(Хmax-Хmin). Отсюда клеточная функция для ячейки С2 будет выглядеть так С2=ЕСЛИ(B2>(МАКС(B$2:B$5)-МИН(B$2:B$5))*90%;"отлично"; ЕСЛИ(B2>МИН(B$2:B$5)+20%*(МАКС(B$2:B$5)-МИН(B$2:B$5));"нормально";"плохо")).
Автонумерация. В ежедневной практике коммерческих организаций требуется формирование прайс-листов на продаваемую продукцию. Обычно, они меняются незначительно. Некоторые товары добавляются другие исчезают, как правило, не надолго. Скорее всего, позже они появятся снова. Организуем автоматическую нумерацию имеющихся товаров таким образом, чтобы последовательные номера присваивались только имеющимся в наличии товарам (количество единиц которых превышает 0). Это позволит поддерживать правильную нумерацию данных, не удаляя (и, следовательно, не вводя затем повторно) из таблицы временно отсутствующие товары. На рис. 4.17-6 слева показан исходный прайс-лист, а справа – он же, но при отсутствии некоторых товаров (столов, тумб).
Видим что строки, содержащие товары, которых нет в наличии, не нумеруются, но последовательность остальных номеров правильная. Здесь A2=ЕСЛИ(C2>0; СЧЁТЕСЛИ(C$1:C2;">0");""), D7=СУММПРОИЗВ(C2:C6;D2:D6). Далее прайс-лист должен быть отпечатан. Чтобы избежать вывода ненумерованных строк, следует воспользоваться операцией фильтрации (см. соответствующий раздел) – установить отбор такого множества данных, в которых отсутствуют строки, не содержащие информации в столбце № или столбце Единиц. Сумма прописью. Построим полезную функцию преобразования суммы (до 9 999 999 руб.), представленной числом, в “сумму прописью”.
Необходимость в этом возникает очень часто при формировании денежных документов. Для указанной цели в отдельный лист (или даже в отдельную книгу) вносятся (рис. 4.17-7) две таблицы. Таблица, связывающая числа от 0 до 99 с соответствующими числительными (десятки и единицы), и аналогичная таблица чисел от 0 до 9 (для сотен). С тем, чтобы не усложнять формируемую функцию необходимостью вставки пробелов между словами, все числительные в таблицах имеют по одному пробелу в конце текста. С целью упрощения формул введем для этих блоков имена: блоку А3:В102 присвоим имя ЕД (от слова единицы), блоку D3:E12 – СТ (от слова сотни). Использование имен позволяет также не указывать в формулах имена листов, где находятся поименованные блоки. На рис. 4.17-7 в клетке В1 представлено исходное число в цифровой форме, а в В2 – результат преобразования. Используемая функция и связи ее компонент с преобразуемым числом приведены на рис. 4.17-9. Она состоит из девяти текстовых составляющих, объединенных знаком сцепления символьных данных “&”. Первая строка преобразует один самый старший седьмой разряд (разряд миллионов) исходного числа с помощью данных, содержащихся в блоке ЕД. Вторая – Замечание. Довольно скучно вводить числа прописью от 1 до 99 в блок ЕД. Это можно сделать довольно быстро, если воспользоваться средствами копирования и преобразования данных. Числительные от 1 до 19, конечно, придется ввести непосредственно. Далее следует ввести слово “двадцать ” и скопировать его в следующие девять строк. Затем “тридцать ” и сделать тоже самое. И так до “девяносто ” включительно. Теперь нужно присоединить к этим словам числительные “один”, “два”, … “девять”. Это удобно сделать так: · Ввести в столбец С указанные числительные рядом с клетками, содержащими слово “двадцать ”, получив, например, такие строки смежных клеток двадцать один, двадцать два и т.п. · Скопировать несколько раз весь блок числительных “один”, “два”, … “девять” вниз, чтобы они стали рядом со словами “тридцать ”, “сорок ” и т.д. · Соединить в столбце D оба слова из столбцов В и С так, что бы двадцать один превратилось в двадцать один. Для этого нужно воспользоваться формулой вида D24=B24&C24, скопировав ее затем вниз до конца таблицы. · Созданные таким образом данные переместить из столбца D на положенное место в столбец В, используя механизм переноса только значений (Правка+Специальная вставка+Вставить+Значения).
4.18. Задачи для самостоятельного решения
Таким образом: Y1=3-3/1,5X при 0£Х<1, ‚ Y2=0,5+2/4X при 1£Х<3, ƒ Y3=5-5/5X при 3£Х<5, „ Y4=0 при 5£Х<6. Окончательно запишем
5-X до Х<5 0 до Х<6. Отсюда получим клеточное выражение для Y(X) Y= ЕСЛИ(X<1;3-2*X; ЕСЛИ(X<3;0,5+0,5*X;ЕСЛИ(X<5;5-X;0))). Такая функция может быть использована, для построения зависимости внутри периода (т.е. для 0£Х < 6). Если же нам требуется сформировать периодическую функцию с неограниченным диапазоном изменения Х, следует так модернизировать выражение, чтобы внутри его аргумент изменялся строго в указанных пределах. Здесь можно воспользоваться функцией ОСТАТ(Х;период), которая возвращает остаток от деления аргумента на период. В нашем случае на шесть – ОСТАТ(Х;6). При этом, хотя само значение Х может изменяться как угодно, результат останется в пределах от 0 до 6. Заменим все значения Х на ОСТАТ(Х;6):
ЕСЛИ(ОСТАТ(Х;6)<3; 0,5+0,5*ОСТАТ(Х;6); ЕСЛИ(ОСТАТ(Х;6)<5; 5-ОСТАТ(Х;6);0))). На рис. 4.19-2 изображена таблица вычисления заданной функции. В столбце А находится аргумент Х, изменяющийся от 0 до 8 с шагом 0,5. В столбце В – функция Y(X). Для самого первого значения Y это B2= ЕСЛИ(ОСТАТ(A2;6)<1;3-2*ОСТАТ(A2;6); ЕСЛИ(ОСТАТ(A2;6)<3;0,5+0,5*ОСТАТ(A2;6); ЕСЛИ(ОСТАТ(A2;6)<5;5-ОСТАТ(A2;6);0))). Для иллюстрации полученного результата с помощью средств деловой графики построим точечную (со значениями, соединенными отрезками) диаграмму Y(X).
Вышесказанное относится только к графику. Сама полученная функция полностью отвечает заданной. В этом легко убедиться и на диаграмме, если уменьшить шаг расчета. Тесты (выберите ответ) 1. В ячейке А1 находится число 1234. Каков будет результат выполнения следующей формулы =ЗНАЧЕН((2*ПРАВСИМВ(ТЕКСТ(A1;"0000");2))&ЛЕВСИМВ(ТЕКСТ(A1;"0000");2))? – 2468, 6812, 2648. 2. Как задать адрес блока ячеек? – Указать: правый верхний и левый нижний углы; левый верхний и правый нижний; все четыре угла блока. 3. Пусть А1=”май”. Какой результат получится после ее следующих преобразований клетки =ПСТР(A1;3;1)&ПСТР(A1;2;1)&ПСТР(A1;1;1)? – “айм”, ”йам”, ”амй”. 4. Имеется три варианта покупки автомобиля стоимостью 10000$: 1). заплатить сразу 10000$. 2) 5000$ сразу и еще по 1000$ раз в год в течение 6-ти лет. 3). Заплатить 8000$ сразу, и еще по 100$ раз в месяц в течение 30 месяцев. Что выгоднее? Решить эту задачу на компьютере, используя финансовые функции, считая что банковская учетная ставка в регионе составляет 10% годовых.
ПРИМЕРЫ ПРАКТИЧЕСКИХ ЗАДАЧ Рассмотрим ряд примеров, разбор которых позволит читателю освоить основные средства Excel. Кроме того, читатель, возможно, обнаружит среди предложенных примеров задачу, похожую на ту, что он решает ежедневно на своем рабочем месте, но делает это вручную. Представленный ниже материал не следует воспринимать как пособие по финансовой математике. Тематика предлагаемых задач часто связана с денежными расчетами просто потому, что их постановка понятна любому читателю. Это, конечно, совершенно не означает, что для такого инструмента не найдется множества технических приложений. Отметим, что некоторые задания могут быть исполнены несколькими, иногда, возможно, и более эффективными, способами. Цель предлагаемого далее материала – не получение самого лучшего решения в каждом конкретном случае, а овладение техникой построения и оформления таблиц. Замечания. 1. Информация, используемая в примерах, носит условный характер и не отражает реального законодательства. 2. Таблицы представлены на рисунках как в нормальном (“результативном”) виде, так и, по возможности, – в формульном виде. Номера рисунков в тексте совпадают с номерами задач. 3. Следует иметь в виду, что данные во многих примерах сопровождаются единицами измерения ($, кг, шт и др.), которые не вводятся непосредственно в клетки таблицы, но устанавливаются с помощью форматирования. @ В связи с тем, что во многих примерах имеются “процентные” данные, напомним, как их использовать. Проценты вводятся в таблицу как десятичные коэффициенты, которым затем придается формат %, либо они сразу вводятся со знаком процента. В Excel число, изображенное со знаком процента, соответствует в сто раз меньшей величине без знака %. То, что, например, выглядит как 20%, на самом деле является 0,2, то, что выглядит как 100%, соответствует 1. Иными словами, это просто разные формы представления одного и того же числа. Пусть нам нужно выделить часть числа, определенную как его некоторый процент. При вычислениях “на бумаге” следует выполнить такие действия искомая_часть_числа=исходное_число * процент_от_числа/100%. В Excel же достаточно формулы вида искомая_часть_числа=исходное_число * процент_от_ числа. Т.е. нужно умножить это число на процент. Делить на 100% нет необходимости. Однако, если это сделать, результат не измениться ведь здесь 100%º1. Например, нужно найти 20% от числа 500: =500*20%=500*0,2=100. Обе формулы в Excel совершено идентичны. Другая ситуация. Пусть нужно вычислить новое значение числа, уменьшенное на некоторый процент (например, учесть скидку). Здесь следует записать так новое_число=исходное_число – исходное_число * процент или короче новое_число=исходное_число * (1–процент). Например, пусть старая цена товара составляет 500 руб., а новая цена имеет скидку в 20%. Определить новую цену товара в рублях =500(1–20%)=500(100%–20%)=500(1–0,2). Все три записи в Excel идентичны. Аналогичным образом вычисляется наценка: новое_число=исходное_число * (1+процент). Наценка в 20% к 500 руб. даст такую новую цену =500(1+20%)=500(100%+20%)=500(1+0,2). Поскольку, обычно, такие данные участвуют в формулах не в качестве констант, а своими адресами (например, А3 и В4), вполне очевидны формулы вида =А3*(1–В4) и =А3*(1+В4) для скидки и наценки. Очевидно также, что превратить одну функцию в другую можно просто изменив знак непосредственно при числе, находящемся в ячейке, содержащей процент (здесь в В4). Во всех случаях следует иметь в виду, что нельзя складывать (вычитать) процент с каким-либо иным значением, кроме процента (коэффициента). Замечание. Владельцы калькуляторов знают, что (при наличии на нем кнопки %) правомочно действие, в котором с собственно данными (например с деньгами) складываются/вычитаются проценты. Например, действие вида 200р+10% повлечет результат равный 220р (т.е. будет начислен желаемый процент), что, как будто, противоречит вышесказанному. Здесь следует учесть, что в калькуляторе имеется специальная операция взятия процента, которая на сам деле выполнила действие вида 200+200*10%/100%. Поскольку в Excel отсутствует подобный механизм начисления процента, мы должны пользоваться известными школьными правилами работы с процентами. ««« В начале рассмотрим простенький пример, который нам поможет выработать подход к проектированию таблиц. На рис. 5.0а слева изображена вся таблица, справа – формулы для столбца D. Пусть требуется выполнить расчет платы за квартиру. Положим она состоит из оплаты за коммунальные услуги (по 2 руб. за квадратный метр площади) и оплаты за газоснабжение (по 3 руб. с каждого проживающего в квартире человека). Здесь реализован очевидный механизм расчета квартплата=площадь * тариф_за_коммунальные_услуги + человек * тариф_за_газ. Или в виде чисел для первой квартиры D3=80*2+4*3.
Поскольку квартир в доме может быть очень много, непосредственный ввод таких формул для каждой из них делает использование компьютера малопродуктивным, если не сказать бессмысленным. По существу, мы применяем его как тривиальный калькулятор. Конечно, этого и не требуется. Нужно использовать не арифметическое, а алгебраическое представление данных, когда они участвуют в формуле не своими непосредственными значениями, а адресами ячеек (т.е. переменными), в которых они находятся. В нашем случае D3=B3*2+ C3*3. Далее следует просто скопировать (воспользовавшись маркером заполнения клетки) первую формулу D3=B3*2+C3*3 во все нижележащие ячейки. В следующей снизу клетке она превратится в D4=B4*2+C4*3, затем в D5=B5*2+C5*3 и т.д. Здесь проявилось чрезвычайно полезное свойство копируемых ссылок – адаптируемость адресных ссылок под новое положение.
Очевидным недостатком нашего решения является его зависимость от изменения тарифов – при их пересмотре придется изменять множество формул. В виду этого, в электронных таблицах все нормативные данные выносят в отдельные области листа (или даже на отдельные листы), обычно, в верхней его части. В нашем случае такими данными являются цены на коммунальное услуги и газ. Разместим их в клетках В2 и D2 (рис. 5.0б), а в формулах вместо констант (2 руб. и 3 руб.) укажем ссылки на эти ячейки. Как и ранее, введем формулу только для первой квартиры (D5=B5*B2+C5*D2), скопировав затем ее вниз. Если поступить таким образом, мы обнаружим что в нижележащих клетках D6, D7 и т.п. получены выражения вида:
D6=B6* B3 +C6* D3, D7=B7* B4 +C6* D4 и т.д. Они неверны (ошибочные значения подчеркнуты). Поскольку при перемещении вниз изменились также адреса, содержащие тарифы, то площадь квартиры №2 перемножается уже не на тариф коммунальных услуг из ячейки В2, а на содержимое пустой клетки В3. Аналогично с оплатой за газ. Это же относится и ко всем другим квартирам. Чтобы избежать нежелательного изменения адресов тарифов, они фиксируются в формулах (“замораживаются”) введением знака $ перед номером строки (D5=B5*B$2+C5* D$2). Копирование такой формулы вниз
D6=B6*B$2+C6*D$2, D7=B7*B$2+C6*D$2 и т.д. уже не повлечет изменения цифры 2 в адресах B$2 и D$2 (результаты изображены на рис. 5.0б).
Ранее нами уже обсуждался вопрос о возможности вставки строк в таблицу и влияние этого действия на поведение итоговых функции. В нашем случае вставка новых данных (новых квартир) между 4-ой и 5-ой и между 8-ой и 9-ой строками будет проигнорирована функцией СУММ(D5:D8). Обеспечить правильную реакцию функции на верхнюю вставку можно, включив заголовок таблицы в область суммирования, т.е. сделать D9=СУММ(D4:D8). Правильную реакцию на дополнение таблицы в нижней ее части можно реализовать (начиная с версии Excel-2000), если установить флажок Расширять форматы и формулы в списках (вкладка Правка). Однако, если (конечно, в сложных случаях) этот механизм не срабатывает, такое дополнение можно осуществлять оставляя пустой самую последнюю (в нашем случае девятую) строку между собственно данными и десятой строкой, где теперь будут вычисляться суммы. Тогда щелчок мышью на строке 9 с последующей вставкой новой строки опустит 9-ю и 10-ю строки ниже и изменит в последней формулу на D11= СУММ(D4:D10), что соответствует нашим целям. Исключить необходимость присутствия пустой строки среди данных можно, если воспользоваться более сложной функцией суммирования (см. вставку @ после раздела 4.16 в главе “Функции рабочего листа”) вида D9= СУММ(D$4:ИНДЕКС(D:D;СТРОКА()–1)), а если вы хотите изъять заголовок таблицы из области суммирования, то D9=СУММ(ИНДЕКС(D:D;5):ИНДЕКС(D:D;СТРОКА()–1)). Теперь допускается вставка новых строк в произвольное место таблицы (например, выделив любую строку и нажав Ctrl+Плюс) не заботясь о правильности осуществления суммирования – оно будет корректным. Больше этого вопроса мы касаться пока не будем и, чтобы не загромождать таблицы, ограничимся применением самой простой функции СУММ(), полагая, что на практике пользователь самостоятельно выберет и применит удобное ему решение. К оформлению таблицы. Для удобства восприятия информации данные снабжены символами, указывающими на единицы измерения. Так клетка В2 имеет пользовательский формат 0,0”р/метр”, клетка D2 – 0,0”р/чел”, клетки В5-В9 – 0”м”, клетки D5-D9 – 0,0”р”. Пример 5.1. Расчеты по вкладам. Построить таблицу вычисления прибыли от инвестирования суммы, равной 1000 (клетка В1), на четыре года в некоторое производство или в банк. Предполагаемая, выплачиваемая ежегодно, норма прибыли должна составить 10%, 15%, 20% и 30% соответственно. Таблица в числовом и формульном (только для столбца В) видах приведена на рис. 5.1. Используемые табличные функции очевидны и реализуют выражение вида прибыль=вклад*норма. Способ исчисления дохода по вкладу здесь соответствует так называемым простым процентам. Пример 5.2. Расчеты по вкладам (сложные проценты). Аналогичная задача, но предполагается, что инвестор не изымает прибыль, а реинвестирует ее снова в дело. Такой механизм начисления дохода определяется термином “сложные проценты” или “капитализация дохода”. Здесь: прибыль=норма*предыдущая_сумма_на_счету сумма=предыдущая_сумма_на_счету + прибыль. Замечание. В этой задаче копирование формул возможно только со второго года (со строки 5). Именно с этого года формулы начинают повторяться. Значение нарастающей суммы можно выяснить и с помощью имеющейся в Excel финансовой функции вычисления будущего значения прибыли с изменяющейся процентной ставкой БЗРАСПИС() сумма=БЗРАСПИС(вклад; нормы_предшествующих_лет). Так, полное ее значение по завершении последнего четвертого года составит величину, равную выражению B7=БЗРАСПИС(B1;A4:A7). На рис. 5.2б изображена таблица с решением той же задачи (и, естественно, с теми же результатами), но с использованием указанной функции. Если не требуется знать значения накопленных вкладов в конце каждого года, можно, вообще, ограничиться только одной формулой из последней ячейки =БЗРАСПИС(B$1; A$4:A7). А если не нужна таблица, то и вообще =БЗРАСПИС(1000;{0,1;0,15;0,2;0,3}).
Пример 5.3. Распределение фонда заработной платы. Создать таблицу распределения фонда заработной платы сотрудников подразделения в соответствии с устанавливаемым руководителем коэффициентом (индивидуальной оценкой качества и ответственности труда). Для определения зарплаты здесь сначала нужно найти “вес” единицы коэффициента в денежном исчислении (т.е. фонд_зарплаты/сумма_коэффициентов), а затем умножить его на индивидуальный коэффициент работника зарплата_работника=фонд/сумма_коэффициентов*коэффициент_работника. Отсюда следует, что прежде нужно найти сумму всех коэффициентов В8=СУММ(B4:B7). Тогда зарплата Петра будет вычисляться по формуле C4=B$1/B$8*B4. И, наконец, подсчитывается сумма всех установленных зарплат C8=СУММ(C4:C7). Как видим, она в точности равна фонду зарплаты (1000), т.е. выражения записаны верно. На рис. 5.3а таблица отображена в числовом и в формульном форматах.
Усложним задачу (рис. 5.3б). Пусть задается не только коэффициент, но и минимальная зарплата для каждого сотрудника. Такая ситуация возможна в случае, например, если фонд заработной платы увеличен и прибавку следует распределить среди сотрудников. При этом не должно получиться так, что кто-то станет получать зарплату меньшую, чем раньше. Эти данные находятся в столбце Прежняя зарплата. Отсюда формула зарплаты работника
=(фонд–сумма_прежних_зарплат)/сумма_коэффициентов*коэффициент_работника+прежняя_зарплата. Таким образом, здесь делится не весь фонд, а только та его часть, которая больше суммы всех прежних зарплат. Для Петра это D4=(B$1–B$8)/C$8 *C4+B4. Остальные формулы (рис. 5.3в) очевидны. Такое решение подразумевает, что выделенный фонд заработной платы не может быть менее суммы прежних зарплат (т.е. менее прежнего фонда оплаты труда). В случае, если он окажется меньше (у нас меньше 590), результаты будут бессмысленны. Если такое обстоятельство возможно, следует учесть его, например, следующим образом D4=ЕСЛИ(B$8>=B$1; (B$1–B$8)/C$8*C4+B4;B$1/C$8*C4).
Здесь, если сумма прежних зарплат больше выделенного фонда, вычисления производятся как и ранее, если нет – фонд делится между всеми работниками пропорционально их коэффициентам независимо от прежней зарплаты.
Пример 5.4. Перераспределение собственности. Создать таблицу перераспределения собственности акционерного общества при приеме новых пайщиков. Положим, существующие (старые) акционеры имеют голоса (столбец С) в управлении предприятием и распределении прибыли в соответствии со стоимостью их пакетов акций (столбец В). Положим также, что фирма испытывает финансовые затруднения (или хочет расширяться) и ей нужны новые инвесторы, которые готовы внести необходимую для поддержания деятельности компании сумму в 700 тыс. рублей (по 400 и 300 тыс. руб. соответственно). Следует определить новые права каждого из новых и старых пайщиков. Строка 4 в таблице является суммой соответствующих столбцов (например, B4=СУММ(B5:B10)). Относительная значимость каждого акционера определяется по формуле вида C5=B5/B$4 для старого пакета акций и формуле E5=D5/D$4 для нового. Таким образом, новые акционеры получают по 32,52% и 24,39% собственности АО, а относительная собственность старых акционеров со
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.012 с.) |

 – рабочие, попавшие в верхний 20%-й участок диапазона изготовленных деталей, получают оценку “отлично”,
– рабочие, попавшие в верхний 20%-й участок диапазона изготовленных деталей, получают оценку “отлично”,

 вставляет слово “млн.” (если миллионы есть). Третья – один разряд сотен тысяч. Четвертая – два следующих разряда из блока ЕД. Пятая – включает слово ”тыс.”, если число содержит тысячи и т. д. В каждой из строк, отвечающей за какие-либо цифры (кроме копеек, которые не нужно преобразовывать в текст), применяется функция ВПР(). Однако чтобы воспользоваться ею, необходимо выполнить сложные действия по извлечению нужных компонент числа, используемых в качестве аргументов функции ВПР(). Подробнее рассмотрим только первую строку. Здесь исходное число, находящееся в ячейке В1, сначала преобразуется в текстовую форму выражением ТЕКСТ(B1; "0000000,00"), чтобы затем выделить из числа отдельные разряды функцией ПСТР(…). В данном случае функция ПСТР(ТЕКСТ(B1; "0000000,00");1;1) извлекает из него фрагмент, начиная с первой позиции длиной в один символ (т.е. самую первую цифру числа). Далее эта цифра из текстовой формы снова обращается в числовую функцией ЗНАЧЕН(…), с тем, чтобы можно было подставить ее в функцию ВПР(…), разыскивающую цифру прописью в блоке ЕД. Таким образом, первая цифра числа 4 345 103,2 преобразуется в слово "четыре".
вставляет слово “млн.” (если миллионы есть). Третья – один разряд сотен тысяч. Четвертая – два следующих разряда из блока ЕД. Пятая – включает слово ”тыс.”, если число содержит тысячи и т. д. В каждой из строк, отвечающей за какие-либо цифры (кроме копеек, которые не нужно преобразовывать в текст), применяется функция ВПР(). Однако чтобы воспользоваться ею, необходимо выполнить сложные действия по извлечению нужных компонент числа, используемых в качестве аргументов функции ВПР(). Подробнее рассмотрим только первую строку. Здесь исходное число, находящееся в ячейке В1, сначала преобразуется в текстовую форму выражением ТЕКСТ(B1; "0000000,00"), чтобы затем выделить из числа отдельные разряды функцией ПСТР(…). В данном случае функция ПСТР(ТЕКСТ(B1; "0000000,00");1;1) извлекает из него фрагмент, начиная с первой позиции длиной в один символ (т.е. самую первую цифру числа). Далее эта цифра из текстовой формы снова обращается в числовую функцией ЗНАЧЕН(…), с тем, чтобы можно было подставить ее в функцию ВПР(…), разыскивающую цифру прописью в блоке ЕД. Таким образом, первая цифра числа 4 345 103,2 преобразуется в слово "четыре". Построить таблицу вычисления и график периодической функции Y(X) в диапазоне двух ее периодов. Варианты заданий приведены на рисунках ниже. Числовые координаты на осях нанести самостоятельно, используя числа натурального ряда (т.е. 0, 1, 2, 3, …).
Построить таблицу вычисления и график периодической функции Y(X) в диапазоне двух ее периодов. Варианты заданий приведены на рисунках ниже. Числовые координаты на осях нанести самостоятельно, используя числа натурального ряда (т.е. 0, 1, 2, 3, …).
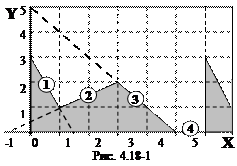 Указания к решению задачи. Положим, требуется построить бесконечную периодическую кусочно-ломанную функцию Y(X). На рис. 4.18-1 изображен ее фрагмент (период функции равен 6). Прежде всего, выразим ее аналитически для одного периода изменения Y(Х) на отрезке от 0 до 6. Напомним, что, если в общем случае уравнение прямой описывается выражением вида Y=A+BX, то значение А равно координате Y точки пересечения прямой с осью ординат. Коэффициент при В равен тангенсу угла наклона прямой (отношению катетов любого прямоугольного треугольника с диагональю образованной исследуемой прямой).
Указания к решению задачи. Положим, требуется построить бесконечную периодическую кусочно-ломанную функцию Y(X). На рис. 4.18-1 изображен ее фрагмент (период функции равен 6). Прежде всего, выразим ее аналитически для одного периода изменения Y(Х) на отрезке от 0 до 6. Напомним, что, если в общем случае уравнение прямой описывается выражением вида Y=A+BX, то значение А равно координате Y точки пересечения прямой с осью ординат. Коэффициент при В равен тангенсу угла наклона прямой (отношению катетов любого прямоугольного треугольника с диагональю образованной исследуемой прямой). 3-2X до Х<1
3-2X до Х<1 Y = ЕСЛИ(ОСТАТ(Х;6)<1; 3-2*ОСТАТ(Х;6);
Y = ЕСЛИ(ОСТАТ(Х;6)<1; 3-2*ОСТАТ(Х;6); На рис. 4.18-3 мы видим кривую, очень похожую на функцию из рис. 4.18-1 благодаря тому, что был выбран шаг (0,5), на который единица делится без остатка. Однако есть и различия, которые будут уменьшаться при уменьшении шага.
На рис. 4.18-3 мы видим кривую, очень похожую на функцию из рис. 4.18-1 благодаря тому, что был выбран шаг (0,5), на который единица делится без остатка. Однако есть и различия, которые будут уменьшаться при уменьшении шага. D5=B5*B2+C5*D2
D5=B5*B2+C5*D2 D5=B5*B$2+C5*D$2
D5=B5*B$2+C5*D$2


