
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наименьших стоимостей.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Приоритетной при заполнении таблицы является не северо-западная клетка, а клетка с наименьшей стоимостью перевозки. Этот метод обычно дает начальный план, более близкий к оптимальному. Рассмотрим каждый из этих методов подробнее. Методом северо-западного угла исходную матрицу перевозок начинают заполнять с левого верхнего угла. В магазин В 1 отправляем с первой базы груз в количестве 20 т, так как потребность этого магазина составляет 20 т, а запас товара на базе 50 т. Потребность магазина В 1 в этом случае удовлетворена полностью, а на первой базе осталось груза 30 т. Поэтому оставшийся товар на первой базе (30 т) отправляют во второй магазин В 2, имеющий потребность в 60 т груза. Оставшуюся потребность магазина В 2 (30 т) удовлетворяют, перевозя груз со второй базы А 2. На базе А 2 остался груз 60 т – его отправляют в магазин В 3 (30 т) и в В 4 (30 т). Потребность магазина В 4 и В 5 удовлетворится с базы А 3. Матрица перевозок примет вид таблицы 7. Таблица 7
В таблице число заполненных клеток равно 7. Их число должно быть m+n – 1 = 3 + 5 – 1 = 7, то есть 7=7. Следовательно, имеем невырожденный опорный план. Найдем стоимость перевозок в полученном плане:
Методом наименьшей стоимости заполнение матрицы перевозок начинается с клетки, имеющей наименьший тариф (с клетки А 2 В 4). В этом случае потребность магазина В 4 составляет 50 т, а запас на базе А 2 90 т. Поэтому в эту клетку следует отправить 50 т. Затем заполняем клетку А 2 В 1, имеющей тариф 5, – 20 т. Следующая клетка с наименьшим тарифом А 3 В 5. Туда отправляем 40 т. и т.д. Получим таблицу 8. Таблица 8
Число заполненных клеток 7. Их число должно быть Стоимость перевозок в полученном плане:
При применении метода наименьшей стоимости стоимость перевозки получилась меньше по сравнению с методом северо-западного угла.
5.3. Распределительный метод решения
Определение. Циклом пересчета в транспортной задаче называется замкнутый многоугольник, одна из вершин которого совпадает со свободной клеткой, для которой образуется цикл, а остальные – заполненными. Вершины соединяются замкнутой ломаной линией, отрезки которой образуют угол 90°. Любой цикл имеет четное число вершин, каждую из которых отмечают знаком. Свободной клетке, для которой выбран цикл, приписывается знак +, остальные знаки чередуются. На рис. 2 дан пример цикла пересчета. В его вершинах указаны номера строк и столбцов клеток, в которых лежат эти вершины.
Рис. 2. Цикл транспортной задачи для клетки (А 1 В 5) таблицы 7.
Свободной клетке, с которой начинается цикл, т.е. клетке (А 1 В 5), присваивают знак +, затем знаки чередуются.
Определение. Алгебраической суммой стоимостей (АСС) свободной клетки называется сумма тарифов перевозок, находящихся в клетках вершин цикла пересчета, взятых с соответствующими знаками в вершинах цикла. Подсчитаем алгебраическую сумму стоимостейАСС свободной клетки (А 1 В 5) транспортной задачи, заданной таблицей 7. АСС(1.5) = 13 + (-8) + 12 + (-4) + 13 + (-22) = +4. Теорема. Если все алгебраические суммы стоимостейсвободных клеток данного базисного решения транспортной задачи неотрицательны, то базисное решение оптимально. Для того чтобы улучшить план, применим симплексный метод. Для этого преобразуем свободное неизвестное с наибольшей по величине отрицательной АСС в базисную переменную, то есть в заполненную клетку. Преобразование достигается с помощью сдвига по циклу пересчета: 1. Находим минимальное из чисел, лежащих в отрицательных вершинах цикла. Обозначим это число D. 2. К числам в положительных вершинах прибавляют D, из чисел в отрицательных вершинах вычитают D. 3. Значения неизвестных клеток старой таблицы (матрицы перевозок), в которых не находились вершины цикла пересчета, переписываются в новую таблицу без изменения. Матрица тарифов остается постоянной. Приведенный метод решения транспортной задачи называется распределительным методом.
Алгоритм распределительного метода решения
Пусть имеется исходное базисное решение транспортной задачи. 1. Для каждой свободной клетки строят цикл пересчета и подсчитывают алгебраические суммы стоимостей. 2. Если среди алгебраических сумм стоимостейАСС есть отрицательные, то план не оптимальный и следует перейти к пункту 3. Если все АСС неотрицательные, то данное базисное решение является оптимальным. Подсчитывают оптимальное значение стоимости перевозок. 3. Среди всех алгебраических сумм стоимостей(АСС) выбирают наибольшую по величине отрицательную АСС и соответствующую ей свободную клетку матрицы перевозок. 4. Для свободной клетки, найденной в п.3, составляют цикл пересчета. Производят сдвиг, преобразовав свободную клетку в базисную. Получают новое базисное решение. Записывают его в таблицу перевозок. 5. Возвратиться к пункту 1 алгоритма.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.43.106 (0.007 с.) |

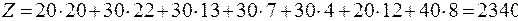 руб.
руб. руб.
руб.




