
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение транспортной задачи распределительным методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для решения задачи воспользуемся исходным базисным решением, полученным методом северо-западного угла (см. табл. 7). 1.
(1,3) АСС = 9 – 7 + 13 – 22 = –7.
(1,4) АСС = 16 – 4 + 13 – 22 = 3.
(1.5) АСС = 13 – 8 + 12 – 4 + 13 – 22 = 4.
(2,1) АСС = 5 – 20 + 22 – 13 = –6.
(2,5) АСС = 10 – 8 + 12 – 4 = 10.
(3,1) АСС = 13 – 8 + 12 – 4 + 13 –22 = 4.
(3,2) АСС = 18 – 13 + 4 – 12 = –3.
(3,3)
АСС = 15 – 7 + 4 – 12 = 0.
Есть три клетки с отрицательными АСС. Решение не оптимальное. 2. Выбираем свободную неизвестную, то есть клетку с максимальной по абсолютной величине отрицательной алгебраической суммой стоимостей: (1,3). 3. В вершинах ее цикла пересчета базисные неизвестные имеют следующие значения
Минимальное значение в отрицательной вершине равно 30. В клетки со знаком + прибавляем 30, со знаком минус – отнимаем 30. Получим:
Количество базисных неизвестных не может измениться. Поэтому клетка (2.3) остается базисной со значением неизвестной равной нолю. Новая матрица перевозок примет вид (табл. 9). Таблица 9
Найдем стоимость перевозок в полученном плане:
Подсчитаем АСС свободных клеток. (1,2): 22 – 9 + 7 – 13 = 7; (1,4): 16 – 4 + 7 – 9 = 10; (1.5): 13 – 8 + 12 – 4 + 7 – 9 = 11; (2.1): 5 – 20 + 9 – 7 = –13; (2.5): 10 – 8 + 12 – 4 = 10; (3.1): 30 – 20 + 9 – 7 + 4 – 12 = 4; (3.2): 18 – 13 + 4 – 12 = –3; (3.3): 15 – 7 + 4 – 12 = 0. Решение не оптимальное. Надо преобразовать неизвестную (2.1). В ее цикле пересчета надо сдвигать на значение неизвестной в клетке (2.3), т.е. на ноль. Получаем новую матрицу перевозок (табл. 10). Таблица 10
Найдем стоимость перевозок в полученном плане:
Подсчитаем АСС свободных клеток: (1.2): 22 – 13 + 5 – 20 = –6; (1.4): 16 – 4 + 5 – 20 = –3; (1.5): 13 – 8 + 12 – 4 + 5 – 20 = –2; (2.3): 7 – 5 + 20 – 9 = 13; (2.5): 10 – 8 + 12 – 4 = 10; (3.1): 30 – 5 + 4 – 12 = 17; (3.2): 18 – 13 + 4 – 12 = –3; (3.3): 15 – 9 + 20 – 5 + 4 – 12 =13. Решение не оптимальное. Составим цикл пересчета для клетки (1.2). Получим новое решение (табл. 11). Таблица 11
Найдем стоимость перевозок в полученном плане:
Подсчитаем АСС таблицы 11: (1.1): 20 – 22 + 13 – 5 = 6; (1.4): 16 – 4 + 13 – 22 = 3; (1.5): 13 – 8 + 12 – 4 + 13 – 22 = 4; (2.3): 7 – 13 + 22 – 9 = 7; (2.5): 10 – 8 + 12 – 4 = 10; (3.1): 30– 5 + 4 – 12 = 17; (3.2): 18 – 13 + 4 – 12 = –3; (3.3): 15 – 9 + 22 – 13 + 4 – 12 = 7. Существует одно значение АСС<0 для клетки (3.2). Составим для нее цикл пересчета. Новое решение имеет вид: Таблица 12
Найдем стоимость перевозок в полученном плане:
Подсчитаем АСС для таблицы 12: (1.1): 20 – 22 + 13 – 5 = 6; (1.4): 16 – 4 + 13 – 22 = 3; (1.5): 13 – 8 + 18 – 22 = 1; (2.3): 7 – 13 + 22 – 9 = 7; (2.5): 10 – 8 + 12 – 4 = 10; (3.1): 30 – 5 + 13 – 18 = 20; (3.2): 15 – 18 + 22 – 9 = 10; (3.3): 12 – 18 + 13 – 4 = 3. АСС всех свободных клеток неотрицательны. Следовательно, получено оптимальное решение и минимальная стоимость перевозок Zmin = 1950 руб. По сравнению с исходным планом (табл. 7), получена экономия за счет оптимизации на Ответ: Оптимальный план дан таблицей 12. Минимальная стоимость перевозок Zmin = 1950 рублей. Получена экономия 390 рублей.
Метод потенциалов
Метод потенциалов является одним из наиболее часто используемых методов уточнения плана перевозок. Каждой строке с номером i в матрице перевозок приписывается числовое значение
где Определение. Сумма потенциалов для свободных клеток называется косвенными тарифами
Соотношение между косвенными тарифами свободных клеток базисного решения и их истинными (заданными тарифами) служат критериями оптимальности решения. Теорема. Достаточное условие оптимальности. Если для всех свободных клеток таблицы перевозок Если есть свободные клетки, для которых Алгоритм решения транспортной задачи Пусть имеется исходное базисное решение. 1. Для каждой строки и столбца матрицы перевозок необходимо задать потенциалы и для каждой базисной (заполненной) клетки записать уравнение вида (16). Получим систему уравнений для потенциалов. 2. Так как заполненных клеток 3. Для каждой свободной строки находят косвенный тариф 4. Если косвенный тариф больше истинного, то переходят к пункту 5. Если косвенный тариф меньше или равен истинному тарифу, то данное базисное решение является оптимальным. 5. Среди разностей между косвенным и истинным тарифами, найденных в пункте 3, выбирают наибольшую. Находят соответствующую ей свободную клетку. 6. Для свободной клетки строят цикл перечета. По нему производят сдвиг, преобразовав свободную клетку в базисную. Получают новое базисное решение. 7. Возвращаются к пункту 1 алгоритма.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.69.176 (0.01 с.) |

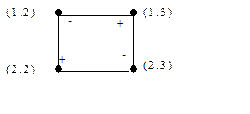 Строим цикл пересчета и подсчитываем АСС для каждой свободной клетки.
Строим цикл пересчета и подсчитываем АСС для каждой свободной клетки.


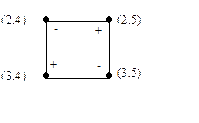
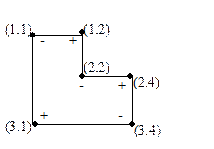
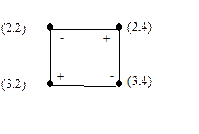
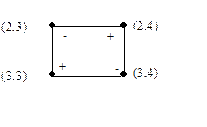

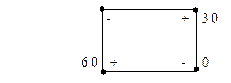
 руб.
руб. руб.
руб.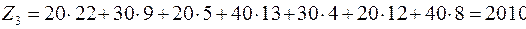 руб.
руб.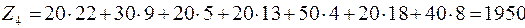 руб.
руб.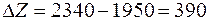 рублей.
рублей.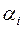 , а каждому столбцу с номером j значение
, а каждому столбцу с номером j значение 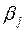 .
. 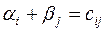 , (16)
, (16) – тариф перевозки.
– тариф перевозки. .
. . (17)
. (17) , то этот план будет оптимальным, причем если
, то этот план будет оптимальным, причем если  , для всех свободных клеток, оптимальный план единственный. Если для некоторых пустых клеток
, для всех свободных клеток, оптимальный план единственный. Если для некоторых пустых клеток 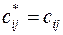 , то оптимальный план не единственный.
, то оптимальный план не единственный. , то рассматриваемый план перевозок не является оптимальным и может быть улучшен пересчетом по циклу, соответствующему одной из клеток, в которых
, то рассматриваемый план перевозок не является оптимальным и может быть улучшен пересчетом по циклу, соответствующему одной из клеток, в которых 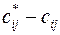 будет максимальной).
будет максимальной). , то соотношение (16) задают систему
, то соотношение (16) задают систему 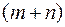 неизвестными. Дополняя ее условием:
неизвестными. Дополняя ее условием:  , получают единственное решение системы потенциалов. Числа
, получают единственное решение системы потенциалов. Числа 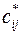 .
.


