Begin // будуємо грані куба (квадрати)

Edge4(A, B, C, D,N1,C_Red); // передня (front)

Edge4(A1,D1,C1,B1,N2,C_Orange); // задня (back)

Edge4(A, D, D1,A1,N3,C_Lemon); // права (right)

Edge4(B,B1,C1,C, N4,C_Aqua); // ліва (left)

Edge4(A, A1,B1,B, N5,C_Green); // верхня (top)

Edge4(C, C1,D1,D, N6,C_Navy); // нижня (bottom)

end;

Викликається в кожному кадрі процедурою

procedure Draw3D;

begin DrawAxis; DrawSolidCube end;

Правильні многранники взаємопов’язані, що можна використати для побудови наступних тіл Платона. З найбільш простої для побудови фігури – куба можна отримати тетраедр, провівши перехресні діагоналі на протилежних гранях куба (рис.6.2). Для виведення грані тетраедра (трикутника) з врахуванням нормалі і кольору процедура аналогічна Edge4

procedure Edge3(V1,V2,V3:V_Array;

N:N_Array;Color:C_Array);

begin glBegin (GL_TRIANGLES);

glColor3fv(@Color);

glNormal3fv(@N); glVertex3fv(@V1);

glVertex3fv(@V2); glVertex3fv(@V3);

glEnd end;

 

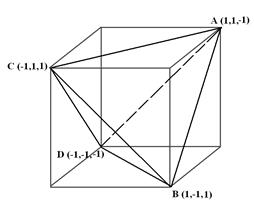
Рис.6.2. Тетраедр, вписаний в куб.

Приклад 6.2. Процедура побудови тетраедра

procedure DrawSolidTetrahedron;

const q=0.577350269; {q=1/sqrt(3);}

// вершини тетраедра // нормалі до граней

A:V_Array=(1,1,-1); N1:N_Array=(q, q, q);

B:V_Array=(1,-1,1); N2:N_Array=(-q,-q, q);

C:V_Array=(-1,1,1); N3:N_Array=(q,-q,-q);

D:V_Array=(-1,-1,-1); N4:N_Array=(-q, q,-q);

Begin // будуємо грані тетраедра (прав.трикутники)

Edge3(A, C, B, N1,C_Red); // 1

Edge3(C, D, B, N2,C_Orange); // 2

Edge3(A, B, D, N3,C_Lemon); // 3

Edge3(A, D, C, N4,C_Aqua); // 4

end;

 

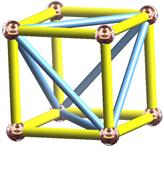
Рис.6.3. Октаедр, вписаний в куб.

Вершини октаедра є центрами граней куба (рис.6.3).

Приклад 6.3. Процедура побудови октаедра

procedure DrawSolidOctahedron;

const q=0.577350269; {q=1/sqrt(3);}

// вершини октаедра // нормалі до граней

A:V_Array=(1,0,0); N1:N_Array=(q, q, q);

B:V_Array=(0,0,1); N2:N_Array=(-q, q, q);

C:V_Array=(-1,0,0); N3:N_Array=(-q, q,-q);

D:V_Array=(0,0,-1); N4:N_Array=(q, q,-q);

E:V_Array=(0,1,0); N5:N_Array=(q,-q, q);

F:V_Array=(0,-1,0); N6:N_Array=(-q,-q, q);

N7:N_Array=(-q,-q,-q);

N8:N_Array=(q,-q,-q);

Begin // будуємо грані октаедра(прав.трикутники)

Edge3(E, B, A, N1,C_Red); // 1

Edge3(E, C, B, N2,C_Orange); // 2

Edge3(E, D, C, N3,C_Lemon); // 3

Edge3(E, A, D, N4,C_Aqua); // 4

Edge3(F, A, B, N5,C_Green); // 5

Edge3(F, B, C, N6,C_Cherry); // 6

Edge3(F, C, D, N7,C_Yellow); // 7

Edge3(F, D, A, N8,C_White) end; // 8

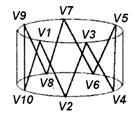
Рис.6.4. Послідовність побудови бічних граней ікосаедра.

Додекаедр та ікосаедр також можна отримати з допомогою відрізання частин куба. Однак існує і більш простий спосіб.

Будуються два кола одиничного радіуса, які лежать на циліндрі на відстані 1 одне від одного (рис.6.4). Кожне з кіл ділиться на 5 рівних частин, причому точки вибираються так, щоб на нижньому колі вершини утвореного правильного п’ятикутника лежали навпроти середин сторін верхнього і навпаки. Отримані на колах точки послідовно з’єднуються, утворюючи пояс із 10 правильних трикутників. Таким чином утворюється 10 вершин ікосаедра. Ще дві точки вибираються над центром верхнього і під центром нижнього п’ятикутників на відстані від них (). З’єднавши ці дві точки з вершинами п’ятикутників, до пояса додається “дах” із 5 правильних трикутників і подібне “дно”, утворюючи ікосаедр (рис.6.5).

Рис.6.5. Побудова ікосаедра з трьох частин.

Координати (x, y) для V₃,V₄,V₈,V₉ обчислюються, як проекції одиничного вектора з кутом 72°, а для V₂,V₅,V₇,V₁₀ з кутом 36 °. Координати (x, y) для інших точок та значення z для всіх точок добре зрозумілі з процесу побудови ікосаедра на наведених вище рисунках.

Координати вершин ікосаедра (список додається до прикладів 6.4 і 6.5).

const cos72= 0.309016994; sin72= 0.951056516;

cos36= 0.809016994; sin36= 0.587785252;

q5div2=1.118033989; { sqrt(5)/2; }

Var // задаємо вершини ікосаедра

V1: V_Array=(0, -1, 0.5);

V2: V_Array=(sin36, -cos36, -0.5);

V3: V_Array=(sin72,-cos72, 0.5);

V4: V_Array=(sin72, cos72, -0.5);

V5: V_Array=(sin36, cos36, 0.5);

V6: V_Array=(0, 1, -0.5);

V7: V_Array=(-sin36, cos36, 0.5);

V8: V_Array=(-sin72, cos72, -0.5);

V9: V_Array=(-sin72,-cos72, 0.5);

V10: V_Array=(-sin36,-cos36, -0.5);

V11: V_Array=(0, 0, q5div2);

V12: V_Array=(0, 0, -q5div2);

Довжина всіх вищенаведених векторів

Рис.6.6. Взаємозв’язок додекаедра та ікосаедра

Додекаедр і ікосаедр пов’язані між собою (рис.6.6). З’єднавши центри граней ікосаедра, одержимо додекаедр. І навпаки: з’єднавши центри граней додекаедра, одержимо ікосаедр. Додекаедр найпростіше побудувати, з’єднавши центри граней ікосаедра. Для обчислення координат вершин додекаедра досить додати і розділити на 3 координати вершин кожної із 20 граней ікосаедра (рис.6.7).

Обчислення координат вершин додекаедра – центрів граней ікосаедра (додається до прикладів 6.4 і 6.5).

Var M1,M2,M3,M4,M5, M6,M7,M8,M9,M10,

M11,M12,M13,M14,M15,M16,M17,M18,M19,M20:V_Array;

procedure Middle(V1,V2,V3:V_Array;var M:V_Array);

begin M[0]:=(V1[0]+V2[0]+V3[0])/3;

M[1]:=(V1[1]+V2[1]+V3[1])/3;

M[2]:=(V1[2]+V2[2]+V3[2])/3 end;