
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Домішкова провідність напівпровідниківСодержание книги
Поиск на нашем сайте
Якщо у власному напівпровіднику деякі атоми замінити атомами з іншою валентністю (наприклад, атоми Ge замінити атомами As), одержимо домішковий напівпровідник. Навіть незначна кількість домішкових атомів (1 домішковий атомна 105 атомів основного напівпровідника) суттєво змінює фізичні властивості напівпровідників. Домішки відіграють подвійну роль. В одних випадках вони є додатковими постачальниками електронів у кристалі (атоми таких домішок називаються донорами), а в інших — центрами захоплення електронів у кристалах (атоми таких домішок називаються акцепторами — одержувачами). Домішкова провідність напівпровідників буває електронна і діркова. 1. Розглянемо домішкову електронну провідність на прикладі германію з домішками атомів миш'яку. Германій — чотиривалентний елемент, а миш'як — п'ятивалентний. Коли в кристалічній решітці атом германію заміщується атомом миш'яку, чотири електрони миш'яку утворюють міцний ковалентний зв'язок з чотирма сусідніми атомами германію, а п'ятий електрон миш'яку, слабо зв'язаний із своїм атомом, легко робиться вільним навіть при кімнатній температурі. Домішкові атоми миш'яку є донорами електронів. Тому електропровідність такого напівпровідника називається електронною, а напівпровідник — n-типу На основі зонної теорії домішкова електронна провідність пояснюється так. Енергія домішкових електронів менша від енергії нижчого рівня зони провідності напівпровідника. Тому енергетичні рівні домішкових електронів (донорні рівні) лежать у забороненій зоні напівпровідника, причому ближче до зони провідності (рис. 8.1.3). Оскільки енергія Е'д дуже мала (наприклад, для кремнію з домішками As
Рис. 8.1.3 Рис. 8.1.4
2. Домішкову діркову провідність германій матиме тоді, коли домішковий елемент буде тривалентний, наприклад, індій. Коли атом германію заміщується атомом індію, останній утворює міцний зв'язок тільки з трьома валентними електронами германію і для утворення повного ковалентного зв'язку не вистачає одного електрона. Тому один з електронів сусіднього атома германію заповнює в атомі індію валентний четвертий зв'язок. Атоми індію при цьому стають центрами захоплення електронів. На місці електрона, який відірвався від германію, з΄являється «позитивна дірка». Ця дірка заповнюється електронами від сусіднього атома германію. Процес повторюється: дірки безладно перемішуються в об'ємі напівпровідника. Під впливом електричного поля дірки утворюватимуть струм. За зонною теорією домішкові акцепторні атоми вносять додаткові незайняті енергетичні рівні, які лежать в області забороненої зони ближче до верхнього рівня валентної зони напівпровідника (рис. 8.1.4). Раніше заповнена валентна зона напівпровідника стає зоною діркової провідності. Такий тип провідності напівпровідника називається дірковою домішковою провідністю або провідністю р-типу. При низьких температурах провідність напівпровідників здійснюється за рахунок домішок, тобто Ед >> Е'д і Еа >> Е'а і для цього потрібна менша енергія. З ростом температури іонізується все більша кількість атомів домішок. Настає температура, при якій всі домішкові атоми іонізовані (область виснаження). При більш високих температурах Т зростання електропровідності пояснюється власною провідністю. Характер залежності електропровідності
Рис. 8.1.5 Практично при дослідженні температурної залежності електропровідності напівпровідників часто користуються не провідністю а просто опором напівпровідника. Для тих температур, для яких формули (7) і (8) мають місце, можна записати: а) для власного напівпровідника
де DЕ — ширина забороненої зони; б) для напівпровідника n-типу
де DЕд — енергія іонізації донорів; в) для напівпровідника р-типу
де DЕа, — енергія іонізації акцепторів; г) для домішкового напівпровідника з обома видами домішок
де DЕ — ширина забороненої зони. Хід роботи Термоелектричний напівпровідниковий прилад, опір якого залежить від температури і який може бути використаний для фіксування зміни температури навколишнього середовища, називається терморезистором або термістором. Напівпровідникові терморезистори, як правило, містять обидва види домішок. Для одержання температурної характеристики терморезистор розміщують у термостаті або в нагрівній пічці на одному рівні з термопарним датчиком, з'єднаним з вимірювальним мостом. Опір напівпровідника при цьому вимірюється мультиметром. Після ознайомлення з лабораторною установкою вимірюють опір терморезистора і відповідну температуру в пічці, починаючи від кімнатної температури і закінчуючи температурою 75-80°С. Результати вимірювань заносять в окрему таблицю.
За одержаним значенням R будують графік R=f(T),а також ln R=f(1/T). Коефіцієнт температурної чутливості В визначають із даних вимірювання опору терморезистора при будь-яких двох температурах Т1 і Т2:
Розділивши почленно вирази (13), одержують
Звідки
Енергію активації знаходять за формулою: DЕ=кВ, де к — стала Больцмана, рівна 1,38.10-23 Дж/К. Обробка експериментальних даних 1. З графіка залежності In R = f (
Одержані результати звіряють із значеннями, відомими з теорії. 2. Визначають коефіцієнт температурної чутливості В терморезистора. 3. Всі розрахунки виконують з допомогою мікроЕОМ. Контрольні запитання 1. Власна і домішкова провідності напівпровідників з точки зору зонної теорії. 2. Температурна залежність провідності напівпровідників. 3. Концентрація вільних носіїв у верхній частині валентної зони і нижній частині зони провідності. Лабораторна робота № 8.2 Мета роботи: ознайомитися з одним із методів визначення концентрації вільних носіїв струму в напівпровідниках та встановити їх природу. Прилади і матеріали: установка для дослідження ефекту Холла в напівпровідниках.
Теоретичні відомості Сукупна дія магнетного і електричного полів істотно ускладнює картину руху носіїв струму в провідних тілах порівняно з дією лише електричного поля. Якщо в другому випадку має місце їх направлений рух – дрейф – зі швидкістю, пропорційною Явище ефекту Холла полягає в тому, що в провіднику зі струмом, розміщеному в зовнішньому магнетному полі, виникає електричне поле, напруженість якого перпендикулярна площині, в якій лежать вектори густини струму і індукції магнетного поля. Зупинимось дещо детальніше на механізмі явища ефекту Холла. На рис. 8.2.1 схематично зображений однорідний ізотропний зразок, через який вздовж осі Х протікає струм І. У додатному напрямку осі Z діє магнетне поле індукції
Рис. 8.2.1
Рис. 8.2.2 Розглянемо зразок напівпровідника у вигляді пластинки, розміри якої подано на рис. 8.2.2. Нехай відомо, що провідність напівпровідника монополярна, для прикладу — діркова. При вибраному напрямку струму вздовж додатного напрямку осі Х швидкість дірок Fл= Fе. (1) Якщо
При достатньо великій довжині пластинки крайовими ефектами можна знехтувати, тому, вважаючи що це поле однорідне, холлівська різниця потенціалів запишеться: Ux = Еb (3) або Uх = В одержану рівність (4) входить середнє значення дрейфової швидкості носіїв заряду, яку можна визначити з електронної теорії дослідним шляхом:
Звідки
де
Підстановкою (7) в (5) одержуємо:
Звідки
Виключивши із співвідношень (4) і (9) швидкість v, одержуємо кінцевий результат:
У співвідношенні (10) вираз
називають сталою Холла. Стосовно викладеної вище найпростішої теорії ефекту Холла; слід зробити деякі суттєві зауваження: У більш строгій теорії співвідношення (11) слід помножити на число g, яке звуть холлівським фактором і яке залежить від особливостей розсіювання дірок і електронів на теплових коливаннях кристалічної ґратки
У випадку розсіювання на заряджених домішках:
При великих концентраціях носіїв заряду g=1. У багатьох випадках, де немає необхідності мати справу з високоточними розрахунками, як і в цій роботі, можна прийняти g=1. Для напівпровідників із змішаною, тобто електронною і дірковою провідністю, під дією сили Лоренца відхиляються як електрони, так і дірки. Кількісне описування цього явища суттєво ускладнюється. Постійна Холла в цьому випадку залежить від концентрації і рухливості носіїв обох знаків, причому вклади електронів і дірок в сукупний ефект — різного знаку. Використання ефекту Холла. 1. Вимірюючи знак і значення постійної Холла (11), можна встановити тип носіїв заряду і їх концентрацію. Одночасно вимірюючи питому електропровідність, є можливість визначити цілий ряд фундаментальних характеристик напівпровідників: ступінь чистоти, енергію активації домішок і ширину забороненої зони, відношення рухливості дірок і електронів і їх ефективні маси.
Рис. 8.2.3 2. Поява холлівської ЕРС використовується в більшості вимірювальних пристроїв і схем автоматики: в магнетометрах (для вимірювання індукції магнетного поля), струмомірах (для вимірювання сили струму, який протікає в кабелях), ватметрах, для перетворення постійного струму в змінний, генерування, модуляції і демодуляції електромагнетних коливань. Для виготовлення холлівських датчиків успішно використовують Ge і Si, однак найкращі результати одержані при використанні InSb, InAs, InAsxP1-x тощо. Хід роботи 1. Ознайомтесь з лабораторною установкою і приведіть її в робочий стан, при цьому кремнієвий напівпровідник розміщується між полюсами постійного магнету з індукцією, яка вказується на лабораторній установці. Там же ви знайдете розміри кремнієвого зразка. Електрична схема установки подана на рис. 8.2.3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.141 (0.008 с.) |

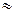 0,054 eB, то за рахунок теплової енергії електрони домішок з донорного рівня переходять у зону провідності напівпровідника.
0,054 eB, то за рахунок теплової енергії електрони домішок з донорного рівня переходять у зону провідності напівпровідника.

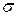 від Т подано на рис. 8.1.5.
від Т подано на рис. 8.1.5.
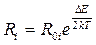 , (9)
, (9) , (10)
, (10)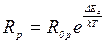 , (11)
, (11)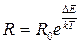 , (12)
, (12)
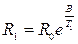 ,
, 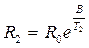 . (13)
. (13) .
.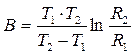 .
. .
.
 , то в першому випадку на дрейфовий рух накладається рух під дією сили Лоренца. У цьому випадку виникають гальваномагнетні явища, найважливішими з яких є ефект Холла.
, то в першому випадку на дрейфовий рух накладається рух під дією сили Лоренца. У цьому випадку виникають гальваномагнетні явища, найважливішими з яких є ефект Холла. . При відсутності магнетного поля вектор напруженості електричного поля направлений вздовж осі X. У цьому випадку різниця потенціалів між точками А і В рівна 0, оскільки точки А і В лежать на одній еквіпотенціальній поверхні. Під дією магнетного поля у напрямку, перпендикулярному до
. При відсутності магнетного поля вектор напруженості електричного поля направлений вздовж осі X. У цьому випадку різниця потенціалів між точками А і В рівна 0, оскільки точки А і В лежать на одній еквіпотенціальній поверхні. Під дією магнетного поля у напрямку, перпендикулярному до 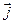 та
та 
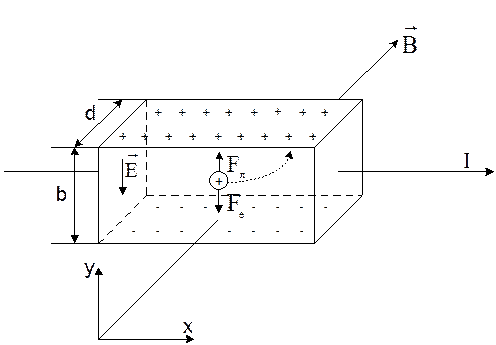
 при відсутності магнетного поля збігається з цим напрямком. При наявності магнетного поля
при відсутності магнетного поля збігається з цим напрямком. При наявності магнетного поля  не стане рівною силі Лоренца Fл:
не стане рівною силі Лоренца Fл: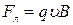 , a Fе=qE, то після підстановки цих значень у рівність (1) знаходимо напруженість холлівського поля:
, a Fе=qE, то після підстановки цих значень у рівність (1) знаходимо напруженість холлівського поля: . (2)
. (2)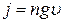 . (5)
. (5) , (6)
, (6)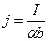 . (7)
. (7) . (8)
. (8) . (9)
. (9) . (10)
. (10)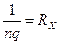 . (11)
. (11)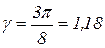 .
. .
.



