
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для зависимой переменнойСодержание книги Поиск на нашем сайте
Одной из задач эк. моделир-я является прогнозир-е зависимой переменной при определённых знач-х независимой переменной. Пусть построено ур-е регрессии: Необходимо на осн. данного ур-я предсказать условное мат. M (Y/xp) переменной Y при Х=хр. Значение Возникает вопрос как сильно может отклониться модельное значение Следовательно случ. величина
Поскольку
В дельнейшем будем исп-ть случ. величину По заданному уравнению значимости α и числу степеней свободы определяем критич. точку Подставим значение вместо t→ P( Выражение в скобках и определяет доверительный интервал для условного мат. ожидания
11.Проверка общего кач-ва ур-ния регрессии. Мерой общего кач-ва ур-ния регрессии,т.е. соотв-ия ур-ния регрессии к стат. данным явл. коэф-т детерминации (R2),кот. определяется по след. формуле: R2=1-( Возведем обе части в квадрат и просуммируем по всем n: (yi-y¯)2 –полная сумма квадратов (меру разброса зависимой переменной относительно среднего значения).
Разделим обе части последнего выражения на левую часть, получим: 1=(
12. На любой экон. показатель чаще всего оказ. влияние не один, а неск. факторов. В этом сл. вместо парной регрессии рассм. мн. регрессия. M(Y/x1, x2,..., xm)=f(x1, x2, …, xm). Ур-е мн. регр. в общем виде Y=f(β, x)+ε, где β= β0, β1, …, βm - вектор теоретических коэфф-в, кот. нужно опред. X=(X1, X2, …, Xm) – в-р незав. перем. Теоретическое лин. ур-е множ. регр-и: Y = β0+ β1X1+ β2X2+…+ βmXm+ε, или в каждом конктреном случае yi= β0+ β1xi1+ β2xi2+…+ βmxim+εi, i= 13. Расчет коэффициентов множ. регр. Представим данные набл-ий и соотв-ие коэф-ты в матр. форме: у1 x11 x12... x1n У= у2, Х= x21 x22... x2n, у3 … … x1m x2m …xmn уn
b0 e1 B= b1, e= e2 … … bm en Ф-цию Q = Тогда их ф-цию Q запишем в виде: Q= Мат-ки док-но, что в.-столбец частных производных ф-ции Q по оцениваемым парам-рам имеет вид:
(
Задача сост-т в том,чтобы по конкретн.выборке найти b0 и b1такие,чтобы построен-ая линия регрессии явл-сь бы наилучш.среди др.,т.е. была бы ближаеш.к точкам наблюд-й по их сов-ти.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.52.43 (0.008 с.) |


 является оценкой M (Y/xp).
является оценкой M (Y/xp). от соответствующего условного мат. ожидания M (Y/xp). Покажем, что случ. величина
от соответствующего условного мат. ожидания M (Y/xp). Покажем, что случ. величина  имеет нормальное распределение, для этого исп-ем формулы для ci и di.
имеет нормальное распределение, для этого исп-ем формулы для ci и di. 
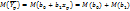





 по выборке определена быть не может, то вместо её подставим несмещённую оценку:
по выборке определена быть не может, то вместо её подставим несмещённую оценку:  , тогда получим выборочную исправленную дисперсию величины
, тогда получим выборочную исправленную дисперсию величины  .
.
 , которое имеет распределение t-стьюдента с числом степеней свободы ν=n-2.
, которое имеет распределение t-стьюдента с числом степеней свободы ν=n-2. ,n-2, кот. удовлетворяет след. условию
,n-2, кот. удовлетворяет след. условию  .
. ,n-2<
,n-2<  ,n-2 =
,n-2 = 
 )=1-α
)=1-α .
. ei2/
ei2/  ei2/
ei2/  . Число степеней свободы для множ. лин. регр-и равно ν=n-m-1. Если n>m+1, то возник. необх-ть оценивания теоретич. коэфф. регр-и. Как и в случае парной регр-и мы будем использ. метод наим. квадратов. Так и для парной регр-и должны вып-ся предпосылки Гаусса-Маркова. Но для множ. регр-и очень существ-ми явл. еще 2 предпосылки. Отсутствие мультиколлинеарности, т.е. м-ду незав. перем-ми должна отсутств. сильная лин. зав-ть. Случ. отклон-е εi, i=
. Число степеней свободы для множ. лин. регр-и равно ν=n-m-1. Если n>m+1, то возник. необх-ть оценивания теоретич. коэфф. регр-и. Как и в случае парной регр-и мы будем использ. метод наим. квадратов. Так и для парной регр-и должны вып-ся предпосылки Гаусса-Маркова. Но для множ. регр-и очень существ-ми явл. еще 2 предпосылки. Отсутствие мультиколлинеарности, т.е. м-ду незав. перем-ми должна отсутств. сильная лин. зав-ть. Случ. отклон-е εi, i=  =b0+b1x1+…+bmxm. Для кажд. наблюд-я мы получим yi=
=b0+b1x1+…+bmxm. Для кажд. наблюд-я мы получим yi=  +ei i=
+ei i= 
 min. Данн. ф-я явл. квадратичной. Необх. усл-ем сущ-я минимума явл. =0 всех ее частичных производных
min. Данн. ф-я явл. квадратичной. Необх. усл-ем сущ-я минимума явл. =0 всех ее частичных производных 
 в матр. форме можно предст. как произв-е
в матр. форме можно предст. как произв-е  - вектор строки на вектор-столбец е. А в свою очередь вектор-столбец е можно записать в виде: е= У-ХВ.
- вектор строки на вектор-столбец е. А в свою очередь вектор-столбец е можно записать в виде: е= У-ХВ. . Приравняем
. Приравняем 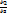 =0, получим форм-лу для вычисл-я оц-к множ. лин. регр.:
=0, получим форм-лу для вычисл-я оц-к множ. лин. регр.: )В=ХТУ => В=(
)В=ХТУ => В=(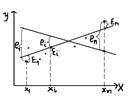
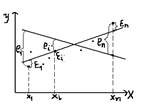 3. Парная линейная регрессия -линейн. фун-ия между условн. мат. ожиданием- М(У/хi)зависимой переменной У и одной независим. переменной Х: (1)М(У/хi)=β0 + β1хi,i=1;n,где хi-знач-я независ. переменной в i-ом наблюдении.Чтоб показать,что кажд.индивидуальн.значение уi отклон-ся от соответств-го условн.мат.ожидания в (1) надо ввести случ-ое слагаемое εi: уi=М(У/хi)+εi=β0+β1хi+εi; i=1;n.←это наз-ся теоретич-й регресс-ой линейн.моделью. β0;β1-теоретич-е коэф-ты регрессии; εi-теоретич-е случ-ое отклонение.Общий вид теоретич-й линейн. регресс-ой модели→ У= β0+β1Х+εi.Чтоб определить значения теоретич.коэф-тов регрессии надо знать ХиУ генеральн.сов-сти,что практич-и невзможно.След-но,по выборке огранич-го объёма (хi;уi),i=1;n мы строим эмпирич-е ур-ние регрессии.(2)
3. Парная линейная регрессия -линейн. фун-ия между условн. мат. ожиданием- М(У/хi)зависимой переменной У и одной независим. переменной Х: (1)М(У/хi)=β0 + β1хi,i=1;n,где хi-знач-я независ. переменной в i-ом наблюдении.Чтоб показать,что кажд.индивидуальн.значение уi отклон-ся от соответств-го условн.мат.ожидания в (1) надо ввести случ-ое слагаемое εi: уi=М(У/хi)+εi=β0+β1хi+εi; i=1;n.←это наз-ся теоретич-й регресс-ой линейн.моделью. β0;β1-теоретич-е коэф-ты регрессии; εi-теоретич-е случ-ое отклонение.Общий вид теоретич-й линейн. регресс-ой модели→ У= β0+β1Х+εi.Чтоб определить значения теоретич.коэф-тов регрессии надо знать ХиУ генеральн.сов-сти,что практич-и невзможно.След-но,по выборке огранич-го объёма (хi;уi),i=1;n мы строим эмпирич-е ур-ние регрессии.(2)  = b0 + b1хi, i=1;n, где
= b0 + b1хi, i=1;n, где 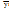 +ei,i=1;n, ei-оценка случайн. отклон-я εi.Т.к. генеральн.сов-ть практически всегда неизв-на,то оцененные парам-ры b0 и b1,от истинных знач-ий β0иβ1.
+ei,i=1;n, ei-оценка случайн. отклон-я εi.Т.к. генеральн.сов-ть практически всегда неизв-на,то оцененные парам-ры b0 и b1,от истинных знач-ий β0иβ1.


