
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет геометрических и электродинамических характеристик облучателя.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчет сводится к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва, и диаграммы направленности облучателя.
Диаграммы направленности рупорной антенны рассчитываются по формулам:
В плоскости H
Рисунок 5 – ДН в плоскости Н
В плоскости E
Рисунок 6 – ДН в плоскости Е
где Ширина луча оптимального пирамидального рупора на уровне 0.5 по мощности (рад) определяется по формулам: В плоскости H
В плоскости E
где значения
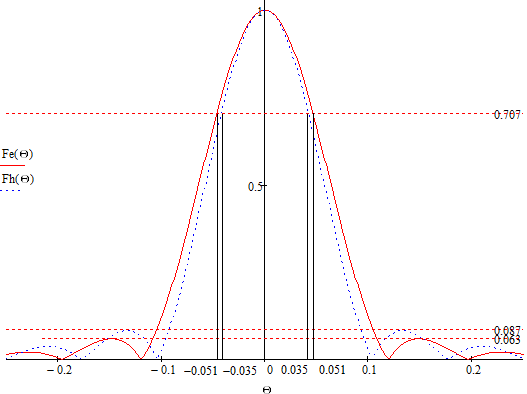
Рисунок 7 – Аппроксимированная нормированная ДН облучателя
Найдем поперечные размеры рупора:
Для оптимального рупора (наибольший КНД) продольные и поперечные размеры связаны между собой соотношениями: в плоскости E
в плоскости H
где Расчет распределения поля в апертуре зеркала. Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам.
где
Распределение поля в апертуре зеркала в плоскости E:
Распределение поля в апертуре зеркала в плоскости H:
На рисунке 8 представлен график распределения поля в апертуре зеркала.
Рисунок 8 – Распределение поля в апертуре зеркала Расчет диаграммы направленности параболической антенны. Инженерный расчёт пространственной ДН параболической антенны часто сводится к определению ДН идеально круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:
где J1 и J2 – цилиндрические функции Бесселя первого и второго порядка; k1=Екр/Еmax=cos(Ψ0/2)Fобл(Ψ0) – коэффициент, показывающий во сколько раз амплитуда возбуждающего поля, на краю раскрыва меньше амплитуды в центре раскрыва, в соответствующей плоскости с учётом различий расстояний от облучателя до центра и края зеркала.
Нормированная ДН зеркальной параболической антенны в плоскости E:
Нормированная ДН зеркальной параболической антенны в плоскости H:
Рисунок 9 - Нормированная ДН зеркальной параболической антенны в плоскости H и E Вектор Пойнтинга (также вектор Умова Пойнтинга) - вектор плотности потока энергии электромагнитного поля, один из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
где Е и Н – векторы напряженности электрического и магнитного полей соответственно:
Рисунок 10 – Вектор Пойнтинга Вычисление шумовых температур антенной системы.
где u=0.02, a1=1- cosn+1Y0=0.914.
Расчет полного коэффициента использования площади, эффективной площади, коэффициента направленного действия и коэффициента усиления антенны. Приближенно коэффициент направленного действия зеркальной антенны определяется выражением:
где S – площадь раскрыва, νрез – результирующий коэффициент использования поверхности.
Точное определение параметров антенны. Коэффициент использования поверхности:
где a1=1- cosn+1Y0=0.931.
При u=0.02 и
Эффективная площадь антенны:
Коэффициент направленного действия:
Коэффициент усиления антенны:
Конструктивный расчет антенны. Выбор конструкции зеркала. С целью уменьшения веса и ветровых нагрузок поверхность зеркала
Рисунок 11 - Конструкция зеркала При такой конструкции зеркала часть энергии просачивается сквозь него, образуя обратное нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении
где Выберем поверхность зеркала сетчатой. Двухлинейная сетка работает удовлетворительно при расстоянии между проводниками меньше 0.1λ, т. е. меньше 1.9·10-3 м и диаметре проводников не менее 0.01λ, т. е. не менее 0,19·10-3 м. 9. Сопоставление расчетного и заданного уровня боковых лепестков, выработка рекомендаций для обеспечения соответствия этих уровней. По рисунку 9 определим ширину диаграммы направленности параболической антенны в плоскости E и H. Рассчитанные параметры:
При большом отклонении боковых лепестков от заданного значения, для снижения УБЛ предлагаются следующие способы: 1. подбирать (изменять) радиус раскрыва зеркала; 2. антенну выполняют неосесимметричной с вынесенным облучателем, незатеняющим основное зеркало; 3. нанесения на антенну радиопоглощающего покрытия (РПП), разработанного на основе композитного материала, обладающего искусственными магнитными свойствами на СВЧ; 4. диэлектрические стержни выбираются конической формы; 5. уменьшают КНД или увеличивают размеры антенны; 6. использование импедансных покрытий.
ВЫВОД В данной курсовой работе был произведен конструктивный расчет зеркальной параболической антенны с облучателем в виде пирамидального рупора, с рабочей частотой 16 ГГц. Для антенны были определены геометрические параметры: диаметр раскрыва, фокусное расстояние и угол раскрыва. Также были рассчитаны полный коэффициент использования площади, эффективная площадь, КУ и КНД антенны. По построенным амплитудным диаграммам направленности параболической антенной по полю в прямоугольной системе координат в плоскостях E и H была определена ширина ДН на уровне половинной мощности в плоскости E и в плоскости H соответственно. Полученные значения соответствовали заданным, поэтому в оптимизации антенны не было необходимости. Уровень боковых лепестков и в первом и во втором случае удовлетворял заданным значениям.
СПИСОК ЛИТЕРАТУРЫ 1. Сазонов Д.М. Антенны и устройства СВЧ. - М.: Высшая школа, 1988. – 432 с. 2. Кочержевский Г.Н. Антенно-фидерные устройства. Учебник для вузов. –М.: Радио и связь, 1989. – 352 с. 3. Хмель В. Ф. Антенны и устройства СВЧ. Сборник задач. – Киев: Вища школа, 1976. – 216 с. 4. Ерохин Г. А. Антенно-фидерные устройства и распространение радиоволн: Учебник для вузов. – М.: Горячая линия-Телеком, 2004. – 491 с.
ПРИЛОЖЕНИЕ А
Оптимальные параметры конического рупора для Е плоскости:
ПРИЛОЖЕНИЕ B
Оптимальные параметры конического рупора для H плоскости:
ПРИЛОЖЕНИЕ C
Рупор пирамидальный:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.108.200 (0.009 с.) |





 ,
,

 определяются по аппроксимированной диаграмме направленности
определяются по аппроксимированной диаграмме направленности  . Для этого построим ее в прямоугольной системе координат (рисунок 7):
. Для этого построим ее в прямоугольной системе координат (рисунок 7):

 .
.

 ,
,




 - длины рупора в соответствующих плоскостях.
- длины рупора в соответствующих плоскостях.

 - диаграмма направленности облучателя,
- диаграмма направленности облучателя, - угол раскрыва,
- угол раскрыва, - текущий угол.
- текущий угол.










 ,
, ,
, ,
, К.
К.


 ,
, ,
, ,
, –точность выполнения профиля зеркала (обычно в пределах 0.4·10-3 – 10-5).
–точность выполнения профиля зеркала (обычно в пределах 0.4·10-3 – 10-5). :
: ,
, ,
, ,015
,015 .
.
 м2.
м2.
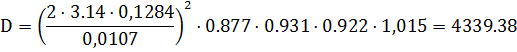

 .
. выполняют перфорированной или сетчатой (рисунок 11).
выполняют перфорированной или сетчатой (рисунок 11).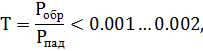
 ,
,  - мощность излучения в обратном направлении и падающая на зеркало, соответственно.
- мощность излучения в обратном направлении и падающая на зеркало, соответственно. -уровень боковых лепестков;
-уровень боковых лепестков; - отклонение боковых лепестков от заданного значения;
- отклонение боковых лепестков от заданного значения; -уровень боковых лепестков;
-уровень боковых лепестков; - отклонение боковых лепестков от заданного значения.
- отклонение боковых лепестков от заданного значения.





