
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет геометрических размеров параболоида.Содержание книги
Поиск на нашем сайте
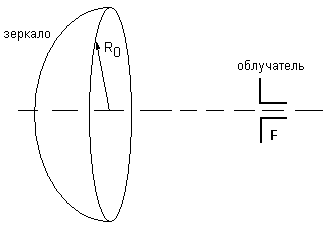
Определение диаметра раскрыва. Зеркальная антенна – направленная антенна, содержащая первичный излучатель (или облучатель) и отражатель антенны в виде металлической поверхности (зеркало). Параболическая зеркальная антенна представлена на рисунке 1.
Рисунок 1 – Зеркальная параболическая антенна В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:
где 2Q0.5 – ширина диаграммы направленности на уровне половинной мощности, рад.; l - длина волны излучаемого (принимаемого) антенной радиосигнала; R0 – радиус раскрыва зеркала (рисунок 1). Однако добиться равномерного возбуждения раскрыва практически не удается. Известно, что КНД зеркальной антенны имеет наибольшую величину в том случае, если амплитуда возбуждающего поля на краю раскрыва составляет не менее одной трети от амплитуды поля в центре раскрыва. Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т.е. ширина главного лепестка в плоскостях в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменение:
где 2QЕ0.5, 2QН0.5 - ширина ДН соответственно в плоскостях Е и Н. В связи с тем, что в задании имеются данные о ширине ДН в обеих плоскостях можно определить диаметр раскрыва dр=2·R0 причем из полученных двух значений диаметра следует выбрать наибольшее. Определим длину волны излучаемого (принимаемого) антенной радиосигнала:
По известным значениям ширины ДН в плоскости H и E найдем радиус раскрыва зеркала. В плоскости H:
В плоскости E:
Для определения диаметра раскрыва выберем R0 = 0,1284 м
2.2 Аппроксимация аналитического вида ДН облучателя функцией вида В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении Ro¤fo КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и от отношения Ro¤fo. При уменьшении отношения Ro¤fo от оптимального КНД уменьшается, так как увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного (рисунок 2); оптимальное значение Ro¤fo определяется по аппроксимированной нормированной ДН облучателя (аппроксимация функцией вида
Рисунок 2 – Варианты размещения облучателя Для пирамидального рупора n=6, т. е. нормированная диаграмма направленности аппроксимируется функцией вида
Рисунок 3 – Аппроксимированная нормированная ДН облучателя
Оптимизация геометрии антенны по максимальному отношению сигнал/шум. Определение угла раскрыва и фокусного расстояния. С точки зрения оптимизации геометрии антенны по максимальному отношению сигнал/шум необходимо произвести следующий расчет. Чувствительность γ определяется формулой
где первые четыре коэффициента не зависят от Ψ0, а γ’ вычисляется:
где Т1 = Тпр +То·(1 - η) + η·Тнер,
То=290о К, u = (0.02 – 0.03) – коэффициент, учитывающий «переливание» части мощности облучателя через края зеркала (примем u=0.02), S - площадь апертуры зеркала, n определяется типом облучателя (для рупорного облучателя n=6), a1=1- cosn+1Y, При n=6 g определяется по формуле:
Построим график функции
Рисунок 4 - График зависимости По максимуму построенной графически функции Для полученного значения a1=1- cos6+146°=0.931,
g=0.877. Фокусное расстояние f0 может быть рассчитано на основе следующего соотношения:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.006 с.) |




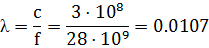
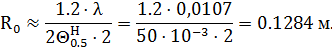

 .
. .
. , где n определяет степень вытянутости ДН облучателя).
, где n определяет степень вытянутости ДН облучателя).
 (рисунок 3).
(рисунок 3).

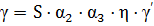 ,
,
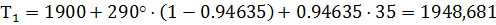 К,
К,
 , по максимуму которого определим угол раскрыва зеркала.
, по максимуму которого определим угол раскрыва зеркала.


 рассчитаем параметры:
рассчитаем параметры: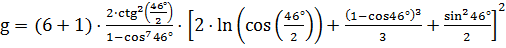 ,
,





