
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотная и фазовая модуляция задающих генераторов передатчиков. Формирование сложных фазоманипулированных и частотно-модулированных сигналов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поскольку мгновенная частота U)(t) с фазой 0(t) сигнала связана соотношением
то частотная и фазовая модуляция взаимозависимы, их объединяют даже общим названием - угловая модуляция. Модуляция называется угловой (УМ), если в колебании вида Благодаря высокой помехоустойчивости угловая модуляция применяется в системах низовой радиосвязи различных диапазонов частот, в радиовещании, в звуковом сопровождении телевизионного вещания, в наземной радиорелейной связи прямой видимости, тропосферной и космической связи. Кроме того, УМ используется в радиотелеметрии, системах радиоуправления, некоторых системах радионавигации и радиолокации. Телеграфные сигналы и цифровая информация в настоящее время передаются преимущественно путем частотной и фазовой манипуляций. При частотной модуляции (ЧМ) мгновенная частота сигнала изменяется по закону модулирующего сигнала, при фазовой (ФМ) - фаза. Поэтому при модуляции тестовым синусоидальным сигналом частотой Ὼ:
Модуляция называется фазовой (ФМ), если индекс модуляции т пропорционален амплитуде модулирующего сигнала UQ и не зависит от его частоты Ὼ. Модуляция называется частотной (ЧМ), если девиация (отклонение) частоты от среднего значения ω0 пропорциональна U Ὼи не зависит от частоты Ὼ, т. е. если индекс модуляции т пропорционален U Ὼ и обратно пропорционален Ὼ/. Таким образом:
где к – коэффициент пропорциональности. При обоих видах модуляции меняется частота колебаний.
При ЧМ девиация частоты При ФМ амплитуда колебания фазы сигнала Таким образом, при обеих видах угловой модуляции - ЧМ и ФМ -меняется как мгновенная частота, так и фаза модулируемого высокочастотного сигнала. Однако, два основных параметра, характеризующих эти виды модуляции - девиация частоты и девиация фазы - по-разному зависят от частоты модулирующего сигнала Ὼ. Существуют прямые и косвенные методы получения ЧМ и ФМ колебаний(сигналов). При прямых методах модулирующее колебание непосредственно воздействует на необходимый для данной модуляции параметр: частоту В первом случае частотный модулятор представляет собой автогенератор, в контур которого включен реактивный элемент, управляемый модулирующим сигналом Прямая фазовая модуляция обычно осуществляется в цепи, через которую проходит РЧ колебание, и сдвиг фазы выходного сигнала изменяется под действием сигнала модуляции Косвенные методы предполагают получение нужного вида угловой модуляции осуществлением другой модуляции и соответствующим преобразованием сигнала. Так как частота и фаза гармонического колебания взаимосвязаны ЧМ колебание можно получить, осуществляя модуляцию по фазе, но при этом необходимо устранить зависимость девиации частоты Δωд от частоты модуляции Ὼ, присущую ФМ.
Девиация фазы на выходе такого устройства Определить вид угловой модуляции можно довольно просто: подать на вход модулятора сигнал
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.81.47 (0.008 с.) |


 в зависимости от модулирующего сигнала изменяется полная фаза (для краткости просто фаза)
в зависимости от модулирующего сигнала изменяется полная фаза (для краткости просто фаза)  ; здесь ω0 — центральная или средняя частота колебания с УМ; Um — неизменная амплитуда колебания.
; здесь ω0 — центральная или средняя частота колебания с УМ; Um — неизменная амплитуда колебания.

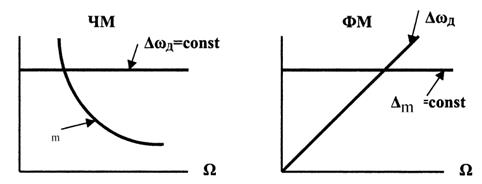
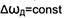 при изменении частоты Ὼ, а девиация фазы сигнала меняется по закону
при изменении частоты Ὼ, а девиация фазы сигнала меняется по закону  .
. ,а мгновенная частота сигнала меняется по закону ωд=
,а мгновенная частота сигнала меняется по закону ωд=  :
: или фазу
или фазу  РЧ колебания.
РЧ колебания.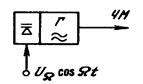
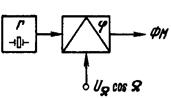
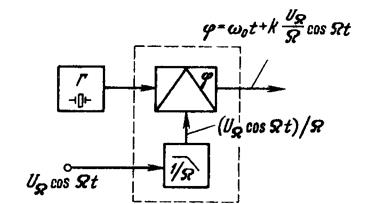 Это нетрудно выполнить, пропустив модулирующий сигнал через цепь с коэффициентом передачи, пропорциональным 1/Ὼ.
Это нетрудно выполнить, пропустив модулирующий сигнал через цепь с коэффициентом передачи, пропорциональным 1/Ὼ. , а девиация частоты при этом
, а девиация частоты при этом 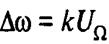 будет зависеть только от амплитуды UῺ, что характерно для ЧМ. Аналогично ФМ колебание можно получить косвенным путем с помощью частотного модулятора и корректирующей цепи на его выходе с коэффициентом передачи, пропорциональным Ὼ.
будет зависеть только от амплитуды UῺ, что характерно для ЧМ. Аналогично ФМ колебание можно получить косвенным путем с помощью частотного модулятора и корректирующей цепи на его выходе с коэффициентом передачи, пропорциональным Ὼ.  В качестве корректирующих цепей можно использовать интегрирующую RС-цепь (рис. 8.5,д) или дифференцирующую RС-цепь (рис. 8.5,е).
В качестве корректирующих цепей можно использовать интегрирующую RС-цепь (рис. 8.5,д) или дифференцирующую RС-цепь (рис. 8.5,е). , а к выходу подключить измеритель девиации частоты. Если девиация частоты зависит только от UῺ и не зависит от частоты, то имеет место частотная модуляция. Если же Δωд оказывается пропорциональной и UῺ, и частоте Ὼ, то модуляция фазовая.
, а к выходу подключить измеритель девиации частоты. Если девиация частоты зависит только от UῺ и не зависит от частоты, то имеет место частотная модуляция. Если же Δωд оказывается пропорциональной и UῺ, и частоте Ὼ, то модуляция фазовая.


