
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Земной эллипсоид, его основные Параметры и соотношения между ними.Содержание книги
Поиск на нашем сайте
Основной задачей геодезии является изучение реально существующей физической поверхности Земли и ее внешнего гравитационного поля. Эта задача решается на основе математической обработки результатов спутниковых, астрономических, геодезических и гравиметрических измерений. По измеренным на земной поверхности углам и расстояниям вычислить с высокой точностью координаты точек не возможно, т.к. неизвестен вид сложной физической поверхности Земли. Целью измерений является определение поверхности. Поэтому в геодезии при решении задач, связанных с математической обработкой наземных измерений, вводится вспомогательная координатная поверхность, которая должна быть наиболее близкой по форме и размерам к действительной поверхности Земли и иметь достаточно простой математический вид, чтобы без затруднений выполнять на ней математическую обработку измерений. В качестве такой поверхности принята поверхность эллипсоида вращения, которая называется общим земным эллипсоидом. Эллипсоид вращения получен путем вращения эллипса вокруг малой оси. Два основных параметра эллипса: большая полуось а=ОЕ, малая полуось в=ОР. Полярное сжатие Связь Геодезическая параллель – линия пересечения поверхности эллипсоида вращения и плоскости перпендикулярной оси вращения. Если плоскость сечения проходит через центр эллипсоида, то геодезическая параллель называется экватором. Геодезический меридиан – часть линии пересечения поверхности эллипсоида вращения и плоскости, содержащей ось вращения, заключенной между полюсами. Все меридианы одинаковы и являются половинками эллипсов. Для того чтобы задать эллипсоид, нужно задать 2 параметра, один из которых должен быть линейным, а остальные можно вычислить. Система прямоугольных пространственных координат За начало координат в этой системе принимается центр эллипсоида – О. Ось OZ направлена по полярной оси, ось ОХ расположена по линии пересечения плоскости Гринвичского меридиана и плоскости экватора Ось OY дополняет систему до правой. Тогда положение точки Q на поверхности эллипсоида будет определено однозначно координатами:
X=OQ1 Y =OQ2 Z=OQ3 Достоинства: 1. Координаты XYZ однозначно определяют положение точки в пространстве. 2. Для ее применения не нужен эллипсоид вращения. Недостатки: 1. Нельзя разделить XYZ. 2. Основная система координат – система плоских прямоугольных координат, но прямого перехода от XYZ к XY – нет. Данная система применяется в выводах формул для обработки спутниковых наблюдений. Система геодезических координат. В этой системе координат положение точки в пространстве определяется тремя координатами: Геодезическая долгота – это двугранный угол, составленный плоскостью начального геодезического меридиана и плоскостью геодезического меридиана проходящего через заданную точку. Долгота измеряется от 0 до 3600 или от 0 до 1800 на восток и запад от гринвичского меридиана. Но долгота определяет положение меридиана, проходящего через точку, а не саму точку. Для определения положения точки на меридиане используется широта. Геодезическая широта – это острый угол составленный плоскостью экватора и нормалью к поверхности эллипсоида, проходящей через заданную точку. Геодезическая широта обозначается буквой В. Широты отсчитываются от экватора к северу и югу и называются северными и южными. Пределы изменения от 0 до 900. Геодезическая высота – отрезок нормали от эллипсоида до точки. Достоинства:1. Координаты BLH однозначно определяют положение точки в пространстве. 2. Эта с.к. позволяет общую задачу по вычислению координат пунктов разделить на 2 подзадачи меньшей размерности. Отдельно определяют BL, отдельно Н. 3. эта система координат связана с системой плоских прямоугольных координат, которая является основной. Билет 22 Преобразование плоских прямоугольных координат Гаусса-Крюгера из одной зоны в другую Задача по преобразованию координат Гаусса-Крюгера возникает в двух случаях: 1.Когда геодезические работы выполняются на границе двух зон.
Когда возникает необходимость перехода от 6º к 3º зонам или к зонам с частным началом координат.
Существует 3 способа преобразования координат: 1.аналитический 2.табличный 3.графический Исходные данные: х(1); у(2); L0(1)(n(1)); L0(2)(n(2)) Найти: х(2), у(2)-? 1. Аналитический способ: путем последовательного перехода.
х, у B, l(1)
Достоинство: 1. Способ универсальный 2. Способ точный, если использовать соответствующие формулы 3. Вычисления можно автоматизировать Недостаток: Если нет компьютера. 2. Табличный способ: основан на применение специальных таблиц для преобразования прямоугольных координат. Этим способом можно решить 3 задачи (при использовании таблиц): 1.Из 6º зоны преобразовать координаты в 3º 2.Из 3 зоны преобразовать координаты в 6º 3.Из 6º зоны преобразовать координаты в 6º Достоинство: Оперативность решения. Недостаток: Невозможна автоматизация Выполняются преобразования координат из государственной в государственную систему. 3. Графический способ: можно применять в зонах взаимного перекрытия (30′ в каждой зоне). Достоинство: Оперативность решения. Недостатки: Применяются в зонах взаимного перекрытия. Низкая точность способа, которая зависит от масштаба.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.115.9 (0.008 с.) |

 Квадрат первого эксцентриситета
Квадрат первого эксцентриситета 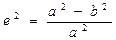 Квадрат второго эксцентриситета
Квадрат второго эксцентриситета 


 ;
;  ;
;  Параметры эллипсоида: а=6378245м, =1/298.9, 1/150.
Параметры эллипсоида: а=6378245м, =1/298.9, 1/150.





