
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вступ до лабораторного практикумуСодержание книги
Поиск на нашем сайте ПОБУДОВА ГРАФІКІВ
В деяких роботах результат досліджень наводиться у вигляді графіка. Щоб графік був зроблений, дотримуються певних правил. Розглянемо їх на конкретному прикладі, Хай, як це вимогається в роботі з вакуумним фотоелементом, одержано кілька значень фотоструму при відповідних значеннях світлового потоку. По цих значеннях складена таблиця:
В таблиці зліва обов язково писати найменування вимірюваної фізичної величини а також вказувати, в яких одиницях ця величина вимірювалась. Відліки по приладах, на основі котрих складена таблиця, можуть бути не цілими, не слід „підганяти“ ці відліки до цілих чисел. За числами, що занесені у таблицю, будується графік. Звичайно на осі абсцис відкладають значення незалежної, тобто тієї величини, що змінюється власне експериментатором в досліді. В розглянутому прикладі нею є світловий потік, який встановлюється зміною відстані джерела світла від фотоелемента. Сила ж фотоструму є залежною величиною. Вона відліковується за мікроамперметром. Залежна зміна відкладається по осі ординат. На малюнку 1 подано приклад нераціональної побудови графіка. Тут є кілька помилок. Оскільки ці помилки є характерними, ми їх розглянемо детальніше. 1. Невірно вибрано масштаб. За цієї причини крива займає тільки частину площини малюнка, тоді як інша частина залишається зайвою. Масштаб треба вибрати так, щоб найбільші значення величин, занесенних в таблицю, виявилися біля кінців осей координат. 2. На осях координат нераціонально позначено масштаб. Для його позначення взято числа з таблиці. Проте масштаб на осях має бути.
Рис. 1. Рис. 2. 3. На графіку не позначено, які величини і в яких одиницях відкладено на осях. Позначення величин треба ставити коло кінців осей, а поблизу – одиниці виміру цих величин. 4. На графіку фактично не позначено експериментальні точки. Положення їх уявляється на перетині пунктирних ліній. Але кожну експериментальну точку треба не тільки позначати, а й обвести кружком, радіус якого дорівнює середній абсолютній похибці в даній серії вимірювань, якщо вони оцінюються в роботі. Допоміжні пунктирні лінії на графіку зображати не треба. 5. На графіку 1 крива проведена так, що вона проходить через всі експериментальні точки. Внаслідок цього крива набуває дещо незвичної форми, тому в неї важко втілити певний фізичний смисл. Треба мати на увазі, що дослід завжди виконується з похибками, тому деякі експериментальні точки на криву не попадуть. Сама ж крива має бути проведена плавно, без необгрунтованих зигзагів, але так, щоб задовольнити одержаним експериментальним точкам. Графік пропонується будувати на міліметровому папері. На рис. 2 побудований графік з дотриманням усіх вищезазначених вимог. Цей графік побудовано за тими ж даними, що і графік на рис. 1. Для з‘ясування усіх згаданих тут зауважень прочитайте ще раз цей параграф, порівнюючи рисунки 1 та 2.
4. КОРОТКІ ВІДОМОСТІ ПРО МІЖНАРОДНУ СИСТЕМУ ОДИНИЦЬ ВИМІРЮВАННЯ ФІЗИЧНИХ ВЕЛИЧИН (SI)
Основу стандарту, що дiє в нашiй кpaїні, складає Мiжнародна система одиниць SI. SI - найбiльш досконала сьогоднi система одиниць. Вона є єдиною i унiверсальною системою, яка охоплює всi областi вимiрювань, встановлює простий i чiткий зв'язок мiж механiчними, тепловими, електромагнiтними i iншими величинами. Основнi одиницi SI
МЕТР (м) - довжина, що дорiвнює l650763,73 довжин хвиль у вакуумi випромiнювання, що вiдповiдає переходу мiж рiвнями 2р10 та 5d5 атому криптону-86. КIЛОГРАМ (кг) - маса, що дорiвнює масi мiжнародного прототипу кi-лограму. СЕКУНДА (с) - час, що дорiвнює 9192631770 пepioдам випромiнювання, яке вiдповiдає переходу мiж двома надтонкими рiвнями основного стану атому цезiю-133. АМПЕР (A) - сила незмiнного струму, який при проходженнi по кожному з двох прямолiнiйних провiдникiв безмежної довжини i незначного кругового перерізу, розмiщених на вiдстанi 1 м один вiд одного у вакуумi, породжував би мiж цими провiдниками силу взаємодii, яка дорiвнює 2×10-7 Н на кожний метр довжини. KEЛЬBIH (K) – 1/273,16 частина термодинамiчної температури потрiйної точки води. КАНДЕЛА (кд) - сила свiтла, випромiнюваного з поверхнi площею 1/600000 м2 полого випромiнювача по перпендикулярному напрямку, при температурi затвердiння платини при тиску 101325 Па. МОЛЬ (моль) - кiлькiсть речовини системи, яка мiстить стiльки ж структурних елементiв, скiльки їx мiститься у нуклiдi вуглецю-12 масою 0,012 кг. При застосуваннi моля структурнi елементи мають бути специфiкованi в групи часток. Кiлькiсть структурних елементiв, що мiститься в одному молi, носить назву числа Авогадро, i воно дорiвнює (6,02252 ± 0,00028)×1023 1/моль. Додатковi одиницi SI Радiан (рад) - кут мiж двома радiусами круга, якi вирiзають на колi дугу, довжина якої дорiвнює радiусовi. Стерадiан (ср) - тiлесний кут з вершиною в центрi сфери, який вирiзає на її поверхнi площу, що дорiвнює квадрату радiусу сфери.
Похiднi одиницi SI
Шунти і додаткові опори Шунт являє собою опір, що вмикається паралельно до вимірювального
механізму (амперметру) в коло вимірювального струму I. На рис. 1: Ri – опір
вимірювального механізму, RШ - опір шунта. Якщо треба збільшити межу вимірювань в n разів(n = I / II), то опір шунта на основі співвідношення II RI = IШ RШ та IШ = I - II буде дорівнювати: RШ = Ri / (n - 1) Шунти виготовляють зі спеціального сплаву – манганіну. Для струмів до 30А шунти звичайно влаштовують всередину приладу, а для струмів понад 30А застосовують зовнішні шунти. Для магнітоелектричних приладів шунти на струми до 30 А виготовляють на кілька меж.
Для розширення меж вимірювання вольтметрів різних систем використовують додаткові опори. Вони ж застосовуються і для розширення меж в інших паралельних колах. Додаткові опори вмикаються з вимірювальним механізмом послідовно. Величина опору, що залежить від заданої межі вимірювань, може бути знайдена на основі слідуючих міркувань.
Нехай на рис. 2 Ri - опір обмотки вимірювального механізму, IH - його номінальний струм. Напруга UH, необхідна для повного відхилення рухомої частини, буде дорівнювати UH = IH Ri. Якщо треба підвищити цю напругу, тобто межу вимірювань вольтметра в m разів шляхом вмикання додаткового опору RД, величина останнього може бути знайдена у такий спосіб: IH Ri m = IH (Ri + RД), звідки RД = Ri (m - 1). Додатковий опір виготовляють із манганінового проводу, намотаного на каркас з ізоляційного матеріалу.
Багатограничні прилади Дуже часто електровимірювальні прилади в процесі заводського виробництва забеспечуються відповідним набором шунтів або додаткових опорів, що інколи розміщуються в самому корпусі приладу, складаючи частину його електричної схеми. Вимірювальний прилад, електричну схему якого можна перемкнути для зміни діапазонів вимірюваної величини, називається багатограничним. Існування багатограничних приладів зумовлено тим, що часто треба з достатнім ступенем точності вимірювати електричні величини в досить широких межах. Багатограничний прилад має вмикатись так, щоб відносна похибка вимірювання була мінімальною, тобто щоб стрілка приладу відхилилась на максимальний кут, але не виходила за межі шкали. Щоб запобігти псуванню приладу, його вмикають на максимальному діапазоні, і після грубого визначення вимірюваної величини переходять на той діапазон, верхня межа якого найближча до значення вимірюваної величини. Чутливість та ціна поділки електровимірювального приладу визначаються таким чином. Чутливістю S електровимірювального приладу до вимірюваної величини x називається похідна від вимірюваного положення покажчика величини за вимірюваною величиною x: S = dφ / dx. Розмірність чутливості залежить від характеру вимірюваної величини. Наприклад, чутливість приладу до струму вимірюється в поділках на ампер (под./А), до напруги - в поділках на вольт (под. /В). Величина, обернена чутливості, називається ціною поділки приладу. Вона показує значення електричної величини, що викликає відхилення на одну поділку.
Похибки приладів
Кожен вимірювальний прилад характеризується тими похибками, що він допускає. Величина, вимірювана взірцевим приладом, приймається за дійсне (істинне) значення. Абсолютною похибкою називається величина, що дорівнює різниці між показанням приладу x/ і істинним значенням вимірюваної величини х. Δxi = x/ - x. Точність вимірювань характеризується відносною похибкою ε1 ε1 = Δx / x/. Іншою важливою характеристикою точності електоровимірювальних приладів є так звана приведена похибка ε2, тобто відношення абсолютної похибки до граничного значення вимірюваної величини x//- найбільшого значення, яке можливо виміряти по шкалі приладу ε2 = Δx / x//. Для приладу з нулем по середині шкали приведена похибка визначається як відношення абсолютної похибки Δx до суми верхньої і нижньої межі вимірювання. Приведена похибка приладів вводиться тому, що відносна похибка приладів не залишається сталою. Приведена похибка приладів пов’язана з точністю електровимірювальних приладів. Згідно з ГОСТ за ступенями точності вимірювань електровимірювальні прилади поділяються на декілька класів: 0,1; 0,2; 0,5; 1; 1,5; 2; 4. Показник класу η визначає приведену похибку вимірювань у відсотках. Отже, абсолютна похибка визначається так: Δx = x//η Наприклад, міліамперметр класу 0,5 зі шкалою у 150 mA дає в будь-якому місці шкали абсолютну похибку ΔI = 150,0 * 0,005 = 0,725 mA Прилади класів 0,1, 0,2, 0,5 застосовують для точних вимірювань і називають лабораторними. В техніці застосовують прилади класів 1, 1,5, 2,5 і 4. Клас приладу звичайно вказується на його шкалі. Точність і чутливість приладу не взаємопов’язані. Бувають прилади високої чутливості, але малої точності, і навпаки.
Ізоляція приладів Безпечність експлуатації вимірювальних приладів вимагає, щоб всі доступні частини приладу були надійно ізольовані від струмопровідних частин, а також щоб була усунена можливість замикання через корпус приладу на землю. Ізоляція кожного приладу перевіряється високою напругою, прикладеною між корпусом і з’єднаними разом затискачами. Випробувальна напруга перевершує робочу інколи в 10 разів і більше. Крім гарантії від пробою на землю ставиться вимога, щоб відстань між струмопровідними частинами та металевим корпусом були не менше нормативної величини. Ці відстані встановлюються окремо для повітря (розрядна відстань) і для поверхні ізоляції (шляхи поверхневих втрат). При цьому береться до уваги, що з часом, внаслідок забруднення, ізоляція погіршується, особливо ізоляція, що знаходиться зовні корпуса.
Рис. 3
Чому одержуються різні значення в межах однієї серії, чому результати вимірювань однієї і тієї ж величини групуються в окремі серії в залежності від методу вимірювання? Відповідь на ці питання можна одержати, познайомившись з теорією похибок та методами обробки експериментальних результатів. Припустимо, що ми одержали величезну сукупність вимірювань однієї і тієї ж величини. Які методи маємо застосувати при вивченні цієї сукупності? Розділ математики, який вивчає системи, що складаються з великої сукупності елементів, називається математичною статистикою. В математичній статистиці і теорії ймовірностей доводиться, що середнє арифметичне значення ряду вимірювань наближається до істинного значення краще, ніж більшість вимірюваних значень. Оскільки часто ми не знаємо істинного значення, то логічно прийняти для нього величину середнього арифметичного <g> <g>= (g1+g2+…+gn)/n, де n – число вимірювань, gi – значення окремих вимірювань. Похибки, що викликають розсіяння результатів коло середнього арифметичного, визначаються випадковими причинами, тому передбачити кожний черговий результат вимірювань неможливо, проте можна передбачити параметри розсіяння результатів коло середнього значення вимірюваної величини. Крім випадкових, існують ще так звані систематичні похибки, які породжуються цілим рядом причин, наприклад, зіпсованістю або недосконалістю приладів, невірним методом вимірювань, властивостями об’єкту вимірювань. Систематичні похибки можуть не впливати на розсіяння результатів вимірювань коло середнього значення, але знайдене середнє значення буде далеко відстояти від істинного. Величина систематичної похибки визначається так: ∆ g = < g > - gіст Це положення наочно представлено на рис. 3. В процесі вимірювань можуть з’явитись грубі помилки (промахи), котрі виникають в разі використання неперевіреного або зіпсованого приладу, недбалого відліку показу, невірного включення приладу, нерозбірливості запису його показань. Від систематичних похибок та промахів має позбутись сам експериментатор, застосовуючи найдосконаліші методи вимірювань та проявляючи особливу ретельність та увагу під час вимірювань. Отже, існують три типи похибок вимірювань: 1. Грубі (промахи). 2. Систематичні. 3. Випадкові. Перші мають бути вилучені повторними вимірюваннями, які проводяться в дещо змінених умовах, дбайливим проведенням експерименту, повторенням експерименту іншим аналогічним приладом і т.д. Систематичні похибки можна усунути застосуванням досконалих приладів, методів вимірювань, нарешті, використанням теоретичних формул, що найбільш правильно описують зв’язок між спостережуваними та шуканими величинами. Випадкові похибки підпорядковуються теорії похибок, але слід пам’ятати, що використання результатів останньої можливе тільки у випадку помітного розсіяння результатів вимірювань. Вимірювальні прилади, що використовуються в лабораторіях, часто дають систематичні похибки, які значно перевершують випадкові.
6.5. Абсолютні і відносні похибки
Абсолютною похибкою окремого виміру ∆ gi називають різницю між виміряним значенням gі і середнім значенням декількох результатів вимірювань: ∆ gi = gі - < g > Абсолютна похибка не характеризує якість вимірювань. Наприклад, абсолютна похибка вимірювання довжини 1мм нічого не говорить нам про його точність. Якщо вимірювалась відстань 10 м, то точність результату слід визнати високою, проте при вимірюванні діаметра кульки в 10 мм така точність явно незадовільна. Для характеристики якості окремого виміру вводять в розгляд відносну похибку: відношення абсолютної похибки окремого виміру до вимірюваної величини. Абсолютні похибки можуть бути як позитивними, так і негативними, тому що частина вимірювань завжди матиме значення, більш за середні, а інша – менші. При спрощеному методі врахування похибок часто діють так. Знаходять відношення середнього значення модуля абсолютної похибки < ∆ g>=(| ∆ g1|+| ∆ g2|+ …+| ∆ gn|)/n до середнього значення вимірюваної величини, і цим відношенням ε (відносною похибкою) характеризують точність вимірювань: ε = < ∆ g> / < g >. Можна знайти таку величину ∆ g, що в середину інтервалу [<g>- ∆ g, <g>+ ∆ g] (1) завжди буде попадати задана частка результатів вимірювань. Звичайно ж, значення ∆ g не дорівнює середньому значенню модуля абсолютної похибки. Якщо ставиться завдання, наприклад, щоб в певний інтервал потрапило 90 % результатів вимірів, то таке значення ∆ g буде істотно більше середнього значення модуля абсолютної похибки. Інтервал (1) називають довірчим інтервалом, а частку результатів, що потрапляють в цей інтервал, надійністю вимірювань. При безмежному числі вимірювань надійність наближаються до так званої довірчої ймовірності. Постає питання: чи можна зменшити інтервал (1), зберігаючи незмінною надійність? Відповідь на це та багато інших питань дає статистична теорія випадкових похибок, з якої розглянемо тільки деякі моменти.
6.6. ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК
6.6.1. Джерела випадкових похибок
Як відзначалося вище, випадковими називають похибки, причини кожної з яких наперед невідомі. Випадкові похибки, як правило, зумовлені великою кількістю причин, що діють при кожному окремому вимірі різним способом. Такі похибки можна звести до мінімуму, але цілком усунути неможливо. Випадкові похибки залежать від дії зовнішніх умов (температура, тиск, вологість і т. п.), що змінюються безперервно. При вивченні випадкових похибок розглядають загальні закономірності, що описують характер розподілу випадкових похибок, розсіяння їх при повторних вимірах та ін.
6.6.2. Середнє значення фізичної величини. Математична ймовірність.
Нехай при вимірюванні деякої фізичної величини g одержано ряд її значень: g1, g2, g3, …, gn, (2) серед яких є і співпадаючі значення. Середнє значення результатів вимірювань визначається за формулою: <g>=(n1g1+n2g2+…)/n, (3) де ni - число вимірювань з результатом gi, так що загальне число вимірювань дорівнює n (n1 + n2 +…= n). Величини n1, n2, … мають зміст чисел, сприятливих для появи окремих результатів вимірів g1, g2, …. Відношення n1/n, n2/n, … будуть характеризувати частоти появи даного значення вимірюваної величини. При необмеженому зростанні числа вимірів частоти прямують до усталених значень, кожне з яких називається ймовірністю появи даного значення Pi
Якщо задані ймовірності появи окремих вимірів, то співвідношення (3) можна переписати у вигляді:
За формулою (5) визначається середнє значення дискретної величини через заданий дискретний розподіл ймовірностей Pi. Проте часто буває так, що розподіл ймовірностей є неперервною функцією вимірюваної величини чи аргументу, від якого залежить вимірювана величина. Нехай, наприклад, значенню g відповідає ймовірність Р(g), а значенню g + dg - ймовірність Р(g) + dР(g), де dg та dР(g) - безконечно малі величини. Такий розподіл ймовірностей називають неперервним. У випадку неперервного розподілу ймовірностей величину dР(g) виражають через похідну р(g): dР(g) = р(g)dg, (6) де р(g) називають законом розподілу ймовірностей фізичної величини g або густиною ймовірностей. В разі неперервного розподілу ймовірностей середнє значення вимірюваної величини подають за допомогою інтегралу:
де інтегрування ведуть за всіма значеннями g. Зауважимо, що при відомому розподілі ймовірностей середнє значення, що обчислюється за виразами (5) та (7), називають математичним сподіванням m фізичної величини g. Різниця тут не термінологічна, а має той смисл, що математичне сподівання при скінченому числі вимірів визначити неможливо, тому що відносна частота появи даної фізичної величини тільки гранично наближається до ймовірності появи даного значення.
6.6.3. Дисперсія
Введемо в розгляд середнє значення квадрату відхилення результатів вимірювання від середнього: Sn2 = ((g1 - <g>)2 + (g2 -<g>)2 + …+(gn -<g>)2)/n (8) При безмежному зростанні числа вимірювань середнє значення випадкової величини <g> наближається до математичного сподівання m, а середнє значення квадрату відхилення від середнього Sn2 - до усталеного значення, яке називається дисперсією даної випадкової величини σ2: σ2 = P1 (g1-m)2 + P2 (g2 – m)2 +…+ Pn (gn – m)2 (n→∞), (9) де m - математичне сподівання величини. При неперервному законі розподілу ймовірностей дисперсію можна подати так:
де інтегрування ведеться за всіма значеннями величини g. Величина σ називається середньоквадратичним відхиленням (стандартним відхиленням або просто стандартом).
6.6.4. Нормальний закон розподілу випадкових похибок (закон Гаусса)
При досить великому числі вимірювань випадкової величини g закон розподілу ймовірностей був доведений Гауссом в такому вигляді:
де g - випадкове значення величини; m - математичне сподівання; σ - стандарт; π = 3,1415925…. При уважному розгляді густини ймовірності (11) здається, що застосування її на практиці неможливо, тому що при конечному числі вимірів величини g залишаються невідомими значення математичного сподівання m і стандарту σ. В дійсності, якщо число вимірів складає не менше 30, то можна користуватись співвідношенням (11), в якому математичне сподівання замінюється середнім арифметичним значенням, а замість стандарту σ використовується величина σn:
6.6.5. Довірча ймовірність та довірчий інтервал
При вимірюваннях важливо знайти ймовірність попадання результату в довірчий інтервал (1), тобто довірчу ймовірність. Довірча ймовірність P, чи надійність вимірювання, це ймовірність того, що будь-який результат виміру не виходить за межі довірчого інтервалу (1). Це можна записати у вигляді: P = P(<g> - Δg<g<<g> + Δg) (13) Вираз (13) свідчить, що результат вимірювань g ймовірністю P ≤1 не виходить за межі довірчого інтервалу. Якщо поставити вимогу більшої надійності, то зрозуміло, що інтервал (1) буде більшим, і навпаки, чим більший довірчий інтервал (1) ми задаємо, тим ймовірніше, що результати вимірів не вийдуть за його межі. Отже, для характеристики величини випадкової похибки мають бути заданими дві величини: величина самої похибки (довірчий інтервал) і величина надійності (довірча ймовірність). Якщо, наприклад, заданий тільки довірчий інтервал без зазначення відповідної довірчої ймовірності, то ми при цьому не знаємо, наскільки надійні наші результати. Для нормального закону розподілу ймовірностей (11) величину довірчого інтервалу звичайно подають в частках стандарту σ:
причому в (11) замість математичного сподівання m використовується середнє арифметичне значення не менше ніж 20 вимірів. Стандарт розраховують по співвідношенню (12). Нижче наведені довірчі ймовірності для цілих значень e:
В науковій літературі звичайно наводять величину середньої квадратичної похибки, що відповідає значенню e =1. В цьому випадку не вказується надійність, тому що вона відома (Р = 0,68).
6.6.6. Визначення надійності при обмеженому числі вимірювань
В умовах фізичного практикуму важко повторити виміри понад 2-5 разів. При такому числі вимірювань розподілом Гаусса скористуватися неможливо. Але виявляється, що існує методика Госсета (Стьюдента), яка придатна для числа вимірювань 2 ≤ n ≤ 20. Розподіл Стьюдента вже при n =7 відрізняється від гауссівського не більше ніж на 3 %. А при n →∞ він фактично переходить в нормальний розподіл. У випадку обмеженого числа вимірювань замість σ(g) із (11) використовують так звану вибіркову середньоквадратичну похибку середньоарифметичного σ(Δg):
Довірчий інтервал при цьому має бути в частках σ(Δg) і називається коефіцієнтом Стьюдента s:
Для різних значень довірчої ймовірності та числа вимірювань існують таблиці коефіцієнтів Стьюдента, наприклад таблиця 1:
Таблиця 1
Відповідно до заданої довірчої ймовірності і конкретної серії вимірювання, за допомогою таблиці 1 та співвідношення (16) обчислюють величину довірчого інтервалу. Кінцевий результат записують у вигляді: g = < g > ± Δg, при P = A %, де А – надійність вимірювань. Той же результат можна подати в такому вигляді: P(<g> - Δg<g<<g> + Δg) = А (тобто ймовірність попадання результатів вимірювань в межі довірчого інтервалу дорівнює А).
6.6.7. Порядок обчислень випадкових похибок при прямих вимірюваннях
Для обчислення випадкових похибок виміри мають бути зроблені щонайменше 2 рази, а краще 3-5 разів, з вилученням явних промахів. Після проведених вимірів роботу проводять у наступній послідовності: 1) обчислюють середньоарифметичне значення < g>= (g1+g2+…+gn)/n; 2) обчислюють абсолютну похибку окремих вимірів gi, а також їх квадрати (Δgi)2;
3) обчислюють вибіркову середньоквадратичну похибку середньоарифметичного σ(Δg); 4) задають довірчу ймовірність (в межах від 0,68 до 0,98) в залежності від умов експерименту; 5) за таблицею коефіцієнтів Стьюдента для даного числа вимірів та заданої надійності обчислюють довірчий інтервал; 6) кінцевий результат вимірювань подають у вигляді: g = <g> ± Δg при Р = А; 7) обчислюють відносну похибку вимірів: ε = Δg / <g>.
6.6.8. Обчислення похибок при непрямих вимірюваннях
В більшості випадків шукану фізичну величину g визначають шляхом обчислень за формулою, в яку підставляють величини x, y, z, …, що вимірюються безпосередньо: g = f (x, y, z, …) Вимірювання величин x, y, z, … проводять незалежно одна від іншої, тому довірчий інтервал функції f(x, y, z, …) визначають законом складання випадкових похибок:
де (17) – закон складання абсолютних незалежних випадкових похибок; (18) – закон складання відносних незалежних випадкових похибок. (Похідні обчислюються при середніх значеннях аргументів.) Існує й інша можливість обчислення довірчого інтервалу при непрямих вимірюваннях для функції декількох аргументів. Кожний аргумент вимірюється n разів. За виміряними аргументами обчислюють n разів шукану функцію. Обчислення похибок вимірів ведуть за схемою для прямих вимірів (для кінцевих значень функції). Кінцевий результат записують: g = <g> ± Δg, при P = A. ВСТУП ДО ЛАБОРАТОРНОГО ПРАКТИКУМУ Лабораторний практикум з фізики ставить за мету закріпити знання, що студенти одержують на лекціях та практичних заняттях, ознайомити студентів в лабораторних умовах з рядом фізичних явищ, вивчити методику вимірювання фізичних величин та їх обробку. Кожна лабораторна робота містить коротку теорію або теоретичні відомості про явище, що вивчається, описання методу вимірювання основних фізичних характеристик явища, порядок виконання лабораторної роботи, а також додаткові запитання, на котрі студент має, підготувати усну відповідь.
1. ОСНОВНІ ПРАВИЛА РОБОТИ В ЛАБОРАТОРІЯХ
1. Користуватися приладами та обладнанням дозволяється тільки у відповідності до інструкції та вказівок. 2. Перед виконанням лабораторної роботи шляхом зовнішнього огляду переконатися в тому, що прилади, вимірювальні установки, обладнання справні. 3. Забороняється працювати в лабораторії самому студенту у відсутності викладача. 4. Остерігатися деталей, що обертаються у вимірювальних установках та не мають охоронного обмеження. 5. При роботі з нагрівачами остерігатися опіків при дотику нагрівача або пари. 6. Забороняється вмикання до електричної мережі чи під’єднання до будь-якого іншого джерела струму не перевіреного електричного кола. Електричні кола перевіряє викладач. Перед ввімкненням всі прилади, що використовуються, мають бути установлені так, щоб при поданні в коло максимально великої напруги через прилад міг йти найменший струм. 7. Після під’єднання до джерела струму забороняється переєднувати електричні прилади, тому що можливе ушкодження електричним струмом. 8. Забороняється залишати без нагляду прилади, увімкнені в електромережу. 9. Після закінчення роботи від’єднати вимірювальне коло від джерела струму, загальну лінію, що з’єднує коло з мережою, погасити в лабороторії світло, перевірити водопровідні крани. 10. Забороняється в лабораторії залишати відчиненими вікна або кватирки. 11. Забороняється використання дуже яскравих джерел світла, при роботі з лазерами не допускається попадання в очі прямих світлових променів.
2. МЕТОДИКА ЛАБОРАТОРНИХ ЗАНЯТЬ
1. Виконання лабораторних робіт відбувається за графіком, що його на вступному занятті видає кожному студенту викладач. 2. Студенти готуються виконувати лабораторні роботи до початку занять. Підготовка складається з ознойомлення з інструкцією до лабораторної роботи, короткого конспектування інструкції в окремому зошиті. Конспект має містити номер роботи та її назву, основні закони та робочі формули (без доведень), малюнок схеми установки, таблиці для занесення результатів вимірювань і наступних розрахунків. Студенти, що не підготувалися до лабораторної роботи, до її виконання не допускаються. 3. Контролює готовність студента до виконання лабораторної роботи викладач. До контролю входить перевірка конспекту роботи, перевірка знання мети роботи, основних явищ і законів, формул, порядку виконання роботи і розрахунку шуканих величин. 4. Після виконання роботи розрахунки мають бути виконані в лабораторії під контролем викладача. При необхідності викладач може запропонувати виконати повторні виміри. 5. Захист лабораторної роботи проводиться після закінчення оформлення звіту. В таблицю звіту мають бути занесені результати вимірювань та розрахунків. Після таблиці має бути наведений приклад розрахунку з указанням розмірностей всіх величин, що входять у розрахункову формулу. 6. Захист лабораторної роботи проводиться на даному або наступному занятті. Студенти, що мають заборгованість з трьох робіт, не допускаються до виконання наступної роботи.
ПРИКЛАД ЗВІТУ ПРО ЛАБОРАТОРНУ РОБОТУ
1. Коротка теорія та метод вимірювання.
В основу роботи покладено один з відомих методів випробування стрілецької зброї за допомогою балістичного маятника. Для одержання непружного удару кулі в маятник запресовано пластилін. Розрахункова основа методу – використання законів збереження енергії і імпульсу. Наводиться схема установки. Закон збереження енергії:
m1v2/2 = (m1 + m2) u2/2 + A (1)
Закон збереження імпульсу:
m2v = (m1 + m2) u2 (2)
В формулах m1 i m2, v i u - відповідно маси кулі та маятника, швидкість кулі та швидкість сумісного руху кулі та маятника після удару; А – робота деформації. Після удару маятник відхиляється за рахунок енергії, що переходить в потенціальну: Wn = (m1 + m2)Rg (1- cosα) = (m1 + m2) u2/2 (3)
де R - довжина балістичного маятника; g - прискорення вільного падіння; α - найбільший кут відхилення маятника. З рівності (3) знаходимо:
u =
Після чого з (2) розраховуємо швидкість кулі:
V = а потім роботу деформації: A = Wk1
2. Результати вимірювань та розрахунків зведемо в таблицю:
Приклад розрахунку:
Wn=(m1 + m2)Rg (1- cosα) = 0,178x 0,8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.013 с.) |












 (4)
(4) = P1g1 + P2g2 + … (5)
= P1g1 + P2g2 + … (5)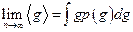 , (7)
, (7) , (10)
, (10)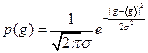 , (11)
, (11) (12)
(12) , (14)
, (14) , (15)
, (15)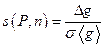 (16)
(16)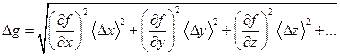 ; (17)
; (17)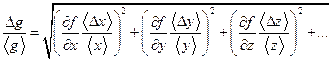 ; (18)
; (18)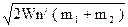 (4)
(4) (5)
(5)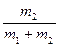
 (6)
(6)


