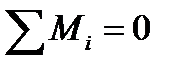Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.1.2 в’язі та їх реакціїСодержание книги
Поиск на нашем сайте
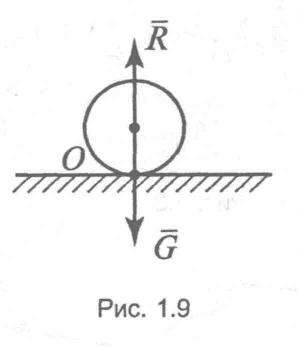
Вільне тіло - це тіло, руху якого ніщо не перешкоджає. Невільне тіло - це тіло, руху якого перешкоджають інші тіла. В'язь - це тіло, що перешкоджає руху інших тіл. Реакція в'язі - це сила, з яким в’язь діє на тіло, перешкоджаючи його руху. Існують такі основні типи в’язей: 1 ) Ідеально гладка поверхня (поверхня столу, рівної дороги). Реакція в’язі напрямлена перпендикулярно поверхні в’язі (рис 1.6, 1.9); 2) Шорстка поверхня. Умовно зображується похилою площиною (рис 1.7). Повна 3) У формі прямого твердого стрижня із шарнірним закріпленням кінців. Реакція стрижня напрямлена уздовж його осі (рис 1.8); 3) у формі кута. Реакція напрямлена перпендикулярно поверхні тіла опори (рис. 1.10); 4) Нитка, мотузка (шнур, трос, ланцюг). Реакція напрямлена уздовж нитки до точки її закріплення (рис 1.11).
Тема 1.2 Системи сил і умови їх рівноваги 1.2.1 Плоска система збіжних сил
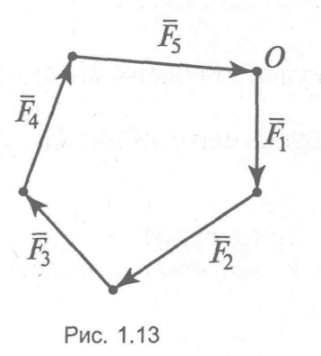
Щоб з'ясувати, чи буде дане тіло знаходитися в рівновазі під дією плоскої системи збіжних сил, необхідно знайти її рівнодійну силу. Якщо рівнодійна дорівнює нулю, система знаходиться в рівновазі. Доведемо два способи визначення рівнодійної сили плоскої системи збіжних сил: геометричний і аналітичний. Геометричний спосіб визначення рівнодійної - побудова силового многокутника: у довільно обрану точку переноситься об'єкт рівноваги, у цю точку міститься початок першого вектора, перенесеного паралельно самому собі; до кінця першого вектора переноситься початок другого вектора, до кінця другого - початок третього і т.д. Якщо побудований силовий иногокутник виявиться незамкнутим, виходить, дана система сил не знаходиться в рівновазі. У цьому випадку вектор рівнодійної сили з'єднає початок першого вектора з кінцем останнього (рис. 1.13, а). Геометрична умова рівноваги плоскої системи збіжних сил, полягає в замкнутості силового многокутника, тобто при побудові силового многокутника кінець останнього вектора збігається з початком першого (рис. 1.13, б).
Аналітичний спосіб визначення рівнодійної: усі сили проектуються на дві взаємно перпендикулярні осі координат, а потім знаходиться алгебраїчна сума проекцій усіх сил на вісь х і вісь у. Якщо алгебраїчна сума проекцій усіх сил дорівнює нулю, дана система сил знаходиться в рівновазі. Аналітична умова рівноваги плоскої системи збіжних сил:
Віссю координат називається довільно обраний спрямований відрізок прямої (рис. 1.14). Проекція сили на вісь координат - відрізок осі, що відтинається перпендикулярами, опущеними з початку і кінця вектора (рис. 1.15).
Пара сил
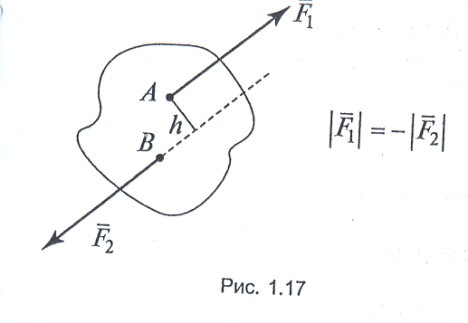
Парою сил називається система двох сил, які дорівнюють по модулю (значенню), протилежні по напрямку та з паралельними лініями дії (не лежачих на однієй прямій) (рис. 1.17).
Обертаючий момент пари сил дорівнює добутку однієї із сил пари на плече:
де h – плече пари сил (перпендикуляр, проведений між лінією дії сил)
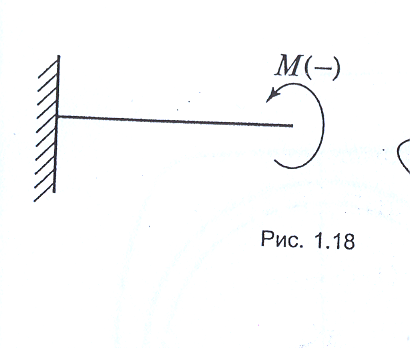
Пари сил на схемах зображуються дугоподібною стрілкою (рис. 1.18).
Рис. 1.19 Дві парі сил називаються еквівалентними, якщо вони виконують на тіло о д н а к о в у дію. У еквівалентних пар сил обертаючі моменти повинні бути однаковими як за величиною, так і за напрямком. Умова рівноваги плоскої системи пар сил: алгебраїчна сума моментів доданків пар сил повинна дорівнювати нулю, тобто
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.30.161 (0.008 с.) |

 реакція розкладається на дві складові: Rn – нормальну та дотичну – RТ відповідно напрямлені по нормалі n і по дотичній Т до поверхні.
реакція розкладається на дві складові: Rn – нормальну та дотичну – RТ відповідно напрямлені по нормалі n і по дотичній Т до поверхні.


 Плоскою системою збіжних сил називається система сил, лінії дії яких лежать в одній площині та перетинаються в одній точці (рис. 1.12).
Плоскою системою збіжних сил називається система сил, лінії дії яких лежать в одній площині та перетинаються в одній точці (рис. 1.12). (система знаходиться в рівновазі)
(система знаходиться в рівновазі)


 (система не знаходиться в рівновазі)
(система не знаходиться в рівновазі)




 Пара сил робить на тіло обертаючу дію, що характеризується обертаючим моментом М.
Пара сил робить на тіло обертаючу дію, що характеризується обертаючим моментом М.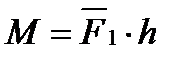
 Пари сил н е м о ж н а замінити однією рівнодійною силою. Пари сил н е м а є проекцій на вісі координат(проекція пари сил на ось - нуль). Якщо на тіло діє декілька пар сил, то їх можна замінити однією рівнодійною парою, момент якої дорівнює алгебраїчній сумі моментів доданків пар сил, що діють на тіло (рис. 1.19):
Пари сил н е м о ж н а замінити однією рівнодійною силою. Пари сил н е м а є проекцій на вісі координат(проекція пари сил на ось - нуль). Якщо на тіло діє декілька пар сил, то їх можна замінити однією рівнодійною парою, момент якої дорівнює алгебраїчній сумі моментів доданків пар сил, що діють на тіло (рис. 1.19):