
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычет в устранимой особой точке равен нулю. ⇐ ПредыдущаяСтр 4 из 4
В задачах 2873-2886 требуется найти вычеты указанны функций относительно ее конечных изолированных особых точек.
№2873.
Решение Очевидно, z=0 и z=1 являются простыми полюсами, т.к.
№2874.
Решение z=2, z=-i.
Тогда
№2875.
Решение
№2876.
Решение
№2877.
Решение
№2878.
Решение
№2879.
Решение
№2880.
Решение
№2881.
Решение
№2882.
Решение
Интеграл от функции
Вычислить интегралы в задачах 2890-2899. №2890.
Очевидно, что в круг радиуса 1 с центром в точке i попадает точка i следовательно по теореме Коши о вычетах
(Сумма состоит из одного слагаемого, т.к. z=-i не лежит внутри L)
тогда
№2891.
Обе точки лежат внутри L.
тогда
№2892.
Обе точки лежат внутри L.
Тогда
№2893.
Все они лежат внутри L.
Тогда
№2894.
Тогда
№2895.
( существенно особая точка )
№2896.
№2897.
Найдем лорановское разложение:
коэффициент при z -1 не равен нулю и таких отличных от нуля коэффициентов бесконечное множество, следовательно точка z=0 – существенно особая точка и
№2898.
коэффициент при z-1 не равен нулю и таких отличных от нуля коэффициентов бесконечное множество, следовательно точка z=0 – существенно особая точка и
Пусть дробно-рациональная функция
не имеет полюсов на действительной оси, причем степень многочлена Qm(z) по крайней мере на две единицы превышает степень многочлена Pm(z)
Где суммы вычетов распространяются на те полюсы функции f(z), которые содержатся в верхней полуплоскости.
Конформные отображения Дробно-линейное отображение (окружность в окружности) представляется 3-мя точками:
разность где встречается ∞ заменяется единицей. 1. №220. Написать какую-либо дробно-линейную функцию, которая переводит круг Решение. На границе данного круга выберем три точки, например, z1=0, z2=2, z3=-2 i. на окружности задается направление обхода, при котором круг оказывается справа. Выберем теперь в плоскости w на действительной оси (которая является границей нижней полуплоскости) три точки w1, w2, w3 таким образом, чтобы при соответствующем обходе границы нижняя полуплоскость оставалась справа. Можно взять, например, w1=0, w2=1, w3=∞. По выбранным трем парам соответственных точек
2. Отобразить полосу a) Рассматривая отображение w1=z-3 i, получим полосу b) с помощью отображения
c) наконец, отображение w3=w2 (угол 3. Найти функцию, отображающую область a) осуществим поворот вокруг нуля на Следовательно, при данном повороте угол b) Рассмотрим отображение 4. Отобразить угол раствора a) b) c)
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.03 с.) |

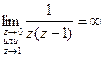 , значит
, значит


 - простые полюсы
- простые полюсы


 - простые полюсы
- простые полюсы


 - простые полюсы
- простые полюсы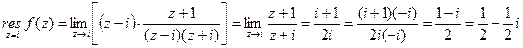
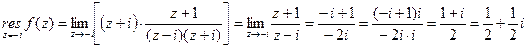


 - полюсы второй кратности
- полюсы второй кратности



 - простые полюсы
- простые полюсы


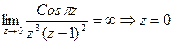 - полюс третьей кратности
- полюс третьей кратности - полюс второй кратности
- полюс второй кратности

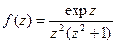
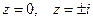
 - полюс второй кратности
- полюс второй кратности - простые полюсы
- простые полюсы




 - простые полюсы
- простые полюсы


 простой полюс
простой полюс - простые полюсы
- простые полюсы
 по кусочно-гладкому контуру Жордина L, лежащему в области D, где функция
по кусочно-гладкому контуру Жордина L, лежащему в области D, где функция  , равен произведению суммы вычетов функции
, равен произведению суммы вычетов функции 

 - простые полюсы
- простые полюсы



 -простые полюсы.
-простые полюсы.



 - полюс второй кратности
- полюс второй кратности - простой полюс
- простой полюс



 - простые полюсы
- простые полюсы





 не существует, следовательно z=0 – существенно особая точка.
не существует, следовательно z=0 – существенно особая точка.
 (коэффициент при z-1)
(коэффициент при z-1)




 - существенно особая точка.
- существенно особая точка.









 . Тогда
. Тогда
 тогда
тогда
 в нижнюю полуплоскость.
в нижнюю полуплоскость.
 - искомое отображение. Это не единственное решение, т.к. точки z1, z2, z3, w1, w2, w3 – произвольные.
- искомое отображение. Это не единственное решение, т.к. точки z1, z2, z3, w1, w2, w3 – произвольные. на верхнюю полуплоскость:
на верхнюю полуплоскость:
 (полоса 0<y<h (h<2π) преобразуется в угол раствора h с вершиной в начале координат)
(полоса 0<y<h (h<2π) преобразуется в угол раствора h с вершиной в начале координат) преобразует полосу
преобразует полосу 
 в угол
в угол  ). В нашем случае
). В нашем случае 
 на область
на область  .
. , это осуществляет функция
, это осуществляет функция 
 преобразуется в
преобразуется в  .
.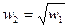 преобразующее угол
преобразующее угол  в угол
в угол  . В нашем случае
. В нашем случае 
 с вершиной в точке z=2+ i ограниченный лучами Arg (z-2-i)=0+2kπ,
с вершиной в точке z=2+ i ограниченный лучами Arg (z-2-i)=0+2kπ,  на нижнюю полуплоскость.
на нижнюю полуплоскость. (переводит угол с вершиной в начале координат)
(переводит угол с вершиной в начале координат) угол в верхней полуплоскости
угол в верхней полуплоскости - искомое отображение.
- искомое отображение.


