
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции и функциональные ряды. Элементарные функции.
Функция
Существуют ли пределы в точке z=0 функций, данных в задачах 2713 – 2716? №2713
№2714
№2715
№2716
№2717 В каких точках комплексной плоскости (Z) не существует предела функции Ответ: во всех точках неположительной части действительной оси (т. к. при движении по часовой стрелке предел равен -π, а против часовой π).
Функция Функции exp z, sin z, cos z определяются с помощью равенств:
Функции exp z, sin z, cos z связаны равенствами:
носящими название формул Эйлера. Для этих функций справедливы также равенства:
для любых z1 и z2. По определению гиперболическим синусом и гиперболическим косинусом называются соответственно функции:
Комплексное число
№2747. Использую формулу (4), представьте в показательной форме комплексные числа: 1) z=-1, |z|=1, arg z=π
3) z=- i,
5) z=1- i,
7)
Все значения логарифма комплексного числа
где Для любых комплексных чисел
(при z1=z2=z≠0, Ln 1=Ln z – Ln z, т. е. Ln 1 = 2k π i (
№2748. Найти все значения нижезаданных выражений: 1)
3) 5)
7)
( 8)
Производная и интеграл. Для того чтобы функция
№2756. Проверить выполнение условий Коши-Римана и найти производную функции в следующих задачах. (2756-2759) w=z2. Пусть z=x+ i y, тогда w=(x+ i y)2=x2-y2+2xyi= Проверим условие Коши-Римана:
№2757. w=z2+2z-1 Пусть z=x+ i y, тогда w=x2-y2+2xy i +2x+2y i -1=x2-y2+2x-1+(2xy+2y) i =u(x;y)+ i v(x;y)
№2758. w=cos 2z Пусть z=x+ i y, тогда Итак,
Поэтому
Условие Коши-Римана выполняется. w´=-2sin 2z
№2761. Доказать, что w=z Im z дифференцируема только в точке z=0, найти w´(0). Проверим условие Коши-Римана. Пусть z=x+ i y, тогда Im z=y и
w´(0)=0+i 0=0 №2760. Доказать, что функция Пусть z=x+ i y, тогда
Условие Коши-Римана не выполняется ни в одной точке, следовательно функция нигде не дифференцируема.
§79. Радиус R сходимости степенного ряда Можно по формуле:
В задачах 2729-2736 определить радиусы сходимости и круг сходимости степенных рядов. №2729.
|Z|<1
№2730
№2731
№2732
|z-(-1)|<1 (круг сходимости) №2733
R=1, |z|<1 (круг сходимости) т.к.
№2734
№2735
№2735
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.41.214 (0.02 с.) |
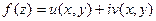 в точке
в точке  имеет предел C = A + i B, тогда и только тогда, когда функции u(x,y) и v(x,y), рассматриваемые как действительные функции двух действительных переменных x и y, имеют в точке (x0,y0) пределы равные соответственно A и B.
имеет предел C = A + i B, тогда и только тогда, когда функции u(x,y) и v(x,y), рассматриваемые как действительные функции двух действительных переменных x и y, имеют в точке (x0,y0) пределы равные соответственно A и B.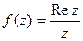 (нет)
(нет) (нет)
(нет) (нет)
(нет)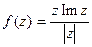 (да)
(да)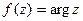 (главное значение аргумента z)?
(главное значение аргумента z)?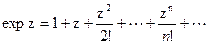
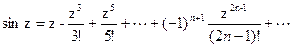

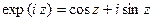
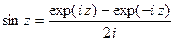
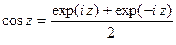
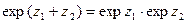
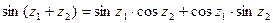

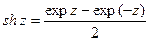
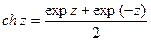
 может быть записано в показательной форме:
может быть записано в показательной форме: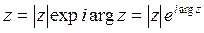 (4)
(4)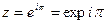
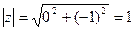 ,
, 
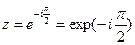
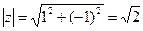 ,
, 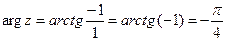
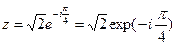
 ,
, 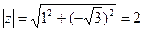 ,
, 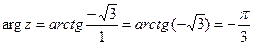
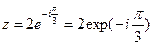
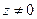 содержатся в равенстве
содержатся в равенстве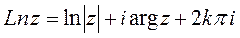 (
( ),
), - главное значение логарифма.
- главное значение логарифма. и α по определению:
и α по определению: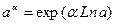
 (
(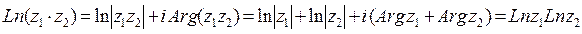
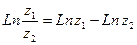
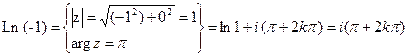 (
( (
(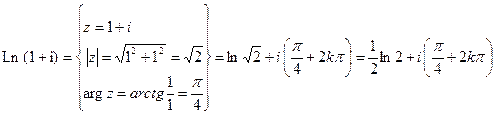 (
(
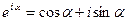 , где α – действительное число)
, где α – действительное число)

 была дифференцируема в точке
была дифференцируема в точке 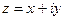 необходимо и достаточно чтобы функции u(x,y) и v(x,y), рассматриваемые как действительные функции от двух действительных переменных x и y, были дифференцируемы в точке (x,y) и чтобы имели место равенства:
необходимо и достаточно чтобы функции u(x,y) и v(x,y), рассматриваемые как действительные функции от двух действительных переменных x и y, были дифференцируемы в точке (x,y) и чтобы имели место равенства: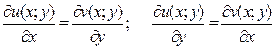 (условие Коши-Римана) При этом производная
(условие Коши-Римана) При этом производная 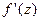 может быть вычислена по формулам:
может быть вычислена по формулам:
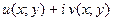 , где u(x;y)=x2-y2, v(x;y)=2xy.
, где u(x;y)=x2-y2, v(x;y)=2xy. т.е. условие Коши-Римана выполняется
т.е. условие Коши-Римана выполняется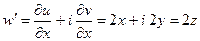
 т.е. условие Коши-Римана выполняется
т.е. условие Коши-Римана выполняется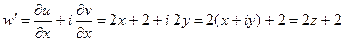
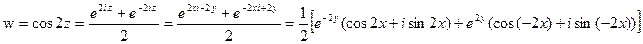

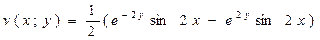
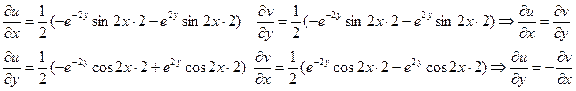
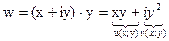


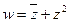 нигде не дифференцируема.
нигде не дифференцируема.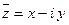 и
и 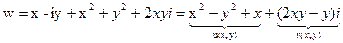

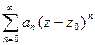 определяется по формуле Коши-Адамара (круг сходимости |z-z0|<R):
определяется по формуле Коши-Адамара (круг сходимости |z-z0|<R):  , причем R=0, если
, причем R=0, если 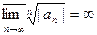 и R=0, если
и R=0, если 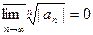 .
.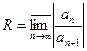
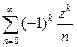 (очевидно z0=0)
(очевидно z0=0)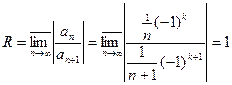

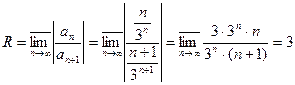 , |z-i|<3 - круг сходимости
, |z-i|<3 - круг сходимости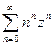

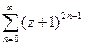


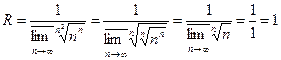
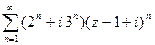

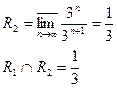
 (круг сходимости)
(круг сходимости)
 - круг сходимости
- круг сходимости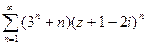

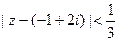 - круг сходимости
- круг сходимости


