
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд Лорана и изолированные особые точки однозначных аналитических функций.Содержание книги
Поиск на нашем сайте
Функция
причем этот ряд единственный и его коэффициенты an определяются по формуле:
где Гр – окружность Если
Пусть
При этом изолированная особая точка z0 функции а) устранимой, если в разложении б) полюсом порядка в) существенно особой точкой если среди коэффициентов an (n = -1; -2;…) содержится бесконечное множество коэффициентов, отличных от нуля. Если
Бесконечно удаленная точка при этом называется бесконечно удаленной изолированной особой точкой функции а) устранимой особой точкой, если в разложении б) полюсом порядка в) существенно особой точкой, если среди коэффициентов an (n =1; 2;…) содержится бесконечное множество коэффициентов, отличных от нуля. Для того чтобы изолированная особая точка z0, конечная или бесконечно удаленная, аналитической функции Если в достаточно малой окрестности изолированной особой точки z0 конечной или бесконечно удаленной, однозначная аналитическая функция Если z0 – существенно особая точка, конечная или бесконечно удаленная, однозначной аналитической функции
В задачах 2830-2851 найти изолированные особые точки аналитической функции и выяснить их характер.
№2830.
Решение Очевидно, особые точки содержатся среди, тех при которых знаменатель обращается в нуль и в ∞.
Отсюда, Т.к. то а №2831
Решение
Очевидно, Т.к. то ∞ - устранимая особая точка.
Функция
№2832
Решение
Т.к.
то
№2833.
Решение.
№2834.
Решение.
№2835.
Решение.
№2836.
Решение
№2837.
Решение.
Поэтому, ∞ - существенно особая точка.
№2838.
Решение Нет конечных особых точек.
№2839.
Решение
№2840.
Решение
№2842.
Решение Нет конечных особых точек.
№2843.
Решение
№2844.
Решение
№2845.
Решение z=1
Нет предела в точке z=1, следовательно z=1 - существенно особая точка.
№2846.
Решение z=1
№2847.
Решение z=2
№2848.
Решение
Т.к. эти точки нельзя заключать в круг радиуса R, то ∞ не является изолированной особенностью.
№2849.
Решение
№2850.
Решение
№2851.
Решение
Точка z0 называется нулём кратности m аналитической функции
где Вычеты и их приложения. Коэффициент a-1 в лорановском разложении однозначной аналитической функции
называется вычетом этой функции относительно точки z0 и обозначается
где В частном случае, когда z0 – полюс функции
если z0 – простой полюс, и по формуле:
если z0 – полюс кратности m>1.
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.152.64 (0.009 с.) |

 , аналитическая в кольце
, аналитическая в кольце 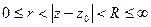 разлагается в этом кольце в ряд Лорана:
разлагается в этом кольце в ряд Лорана: ,
, ,
, .
. , то в этой области она представляется в виде суммы ряда Лорана:
, то в этой области она представляется в виде суммы ряда Лорана: .
.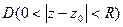 . В этой области ее можно представить в виде суммы ряда Лорана:
. В этой области ее можно представить в виде суммы ряда Лорана: , если в этом разложении коэффициенты
, если в этом разложении коэффициенты  для n=-(m+1);-(m+2);…, причем полюс называется простым, если m=1 и кратным, если m>1.
для n=-(m+1);-(m+2);…, причем полюс называется простым, если m=1 и кратным, если m>1.  , причем полюс называется простым, если m=1 и кратным, если m>1.
, причем полюс называется простым, если m=1 и кратным, если m>1. , такая что
, такая что  .
.
 .
. ,
, - простые полюса,
- простые полюса, ∞ - устранимая особая точка.
∞ - устранимая особая точка.
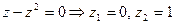
 - простые полюсы.
- простые полюсы. ,
,
 - устранимая особая точка.
- устранимая особая точка.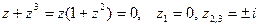 , причем
, причем ,
, – простые полюсы.
– простые полюсы.

 – простой полюс.
– простой полюс. – полюс второй кратности.
– полюс второй кратности.
 – устранимая особая точка.
– устранимая особая точка. полюс третьей кратности.
полюс третьей кратности.
 – устранимая особая точка.
– устранимая особая точка.
 – простой полюс,
– простой полюс,  – полюсы второй кратности.
– полюсы второй кратности.
 – устранимая особая точка.
– устранимая особая точка. – не существует, т.к. не существует
– не существует, т.к. не существует  ∞ - существенно особая точка.
∞ - существенно особая точка.
 – устранимая особая точка.
– устранимая особая точка. – не существует, т.к. не существует пределов при
– не существует, т.к. не существует пределов при 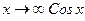 и при
и при  .
.
 – не существует, следовательно ∞ - существенно особая точка.
– не существует, следовательно ∞ - существенно особая точка.
 – устранимая особая точка.
– устранимая особая точка. не существует, следовательно ∞ - существенно особая точка.
не существует, следовательно ∞ - существенно особая точка.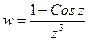
 – полюс третьей кратности
– полюс третьей кратности не существует, следовательно ∞ - существенно особая точка.
не существует, следовательно ∞ - существенно особая точка.
 не существует, следовательно ∞ - существенно особая точка.
не существует, следовательно ∞ - существенно особая точка.
 ∞ – полюс третьей кратности.
∞ – полюс третьей кратности. не существует, следовательно z=0 - существенно особая точка (см. №2838, 2837, 2842).
не существует, следовательно z=0 - существенно особая точка (см. №2838, 2837, 2842).

 – простые полюсы.
– простые полюсы. не существует, следовательно ∞ - существенно особая точка.
не существует, следовательно ∞ - существенно особая точка.

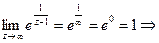 ∞ - устранимая особая точка.
∞ - устранимая особая точка.
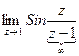 не существует, следовательно z=1 – существенно особая точка.
не существует, следовательно z=1 – существенно особая точка.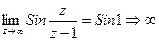 - устранимая особая точка.
- устранимая особая точка.
 не существует, следовательно z=2 – существенно особая точка.
не существует, следовательно z=2 – существенно особая точка. ∞ - устранимая особая точка.
∞ - устранимая особая точка.



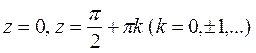
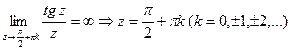 - простые полюсы.
- простые полюсы. - устранимая особая точка.
- устранимая особая точка.

 - устранимая особая точка.
- устранимая особая точка. - простые полюсы.
- простые полюсы.

 - полюс второй кратности.
- полюс второй кратности. - простые полюсы.
- простые полюсы. ,
, , причем нуль называется простым, если m =1, и кратным, если m>1.
, причем нуль называется простым, если m =1, и кратным, если m>1. ,
, (начальные буквы res от французского слова residu – остаток). Вычет через интеграл выражается формулой:
(начальные буквы res от французского слова residu – остаток). Вычет через интеграл выражается формулой: ,
, - окружность,
- окружность, 
 ,
, ,
,


