
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория механизмов и машин: Конспект лекцийСодержание книги
Поиск на нашем сайте
УДК 621.01 (075) ББК 34.44я 73 Ф33
Рецензенты: А.В. Бородин, д-р техн. наук, проф., зав. кафедрой ТММ и ДМ Омского государственного университета путей сообщения; В.Н. Никитин, канд. техн. наук, проф. Сибирской автомобильно- дорожной академии
Фёдоров Н.Н. Ф33 Теория механизмов и машин: Конспект лекций. Омск: Изд-во ОмГТУ, 2005. 60с. В конспекте лекций излагается основное содержание курса теории механизмов и машин, включающее структуру, кинематический, кинетостатический и динамический анализ механизмов, а также кинематику зубчатых механизмов и геометрию эвольвентного зубчатого зацепления. Предназначен для студентов дистанционной формы обучения.
Печатается по решению редакционно-издательского совета Омского государственного технического университета
© Н.Н. Фёдоров, 2005 © Омский государственный технический университет, 2005
ОГЛАВЛЕНИЕ Предисловие.…...…………………………………………………………………........4 Введение.……………………………………………………………………………......5 1. Структура плоских механизмов…………………………………………….…….6 1.1. Классификация плоских кинематических пар…………………………….…......6 1.2. Расчёт подвижности плоского механизма…………………………………..…....8 1.3. Структурная классификация механизмов………………………………….….....9 1.4. Замена высших пар в плоских механизмах…………………………………..…12 1.5. Избыточные (повторяющиеся) связи и местные подвижности в механизмах. 12 2. Кинематика зубчатых механизмов…………………………………………........14 2.1. Понятие о передаточном отношении………………………………………........14 2.2. Передаточное отношение простой зубчатой передачи………….……….…….15 2.3. Кинематика зубчатых механизмов с неподвижными осями колёс……………16 2.4. Кинематика механизмов планетарного типа.……………………………….…..18 3. Эвольвентное зубчатое зацепление..…………….………………………………22 3.1. Основной закон зацепления.………………………………………………….….22 3.2. Эвольвента окружности, её свойства и уравнение.………………………….…23 3.3. Элементы зубчатого колеса.……………………………………………………..25 3.4. Элементы и свойства эвольвентного зацепления.………………………….…..26 3.5. Методы изготовления зубчатых колёс…………………………………………..28 3.6. Геометрия реечного производящего исходного контура……………………....29 3.7. Подрез зуба колеса и его предотвращение………………………………….…..31 3.8. Качественные характеристики эвольвентного зацепления……………….…....33 3.9. Назначение коэффициентов смещения для нарезания зубчатых колёс….........37 3.10.Расчёт геометрических размеров зубчатых колёс……………………………...37 4. Кинематика механизмов с низшими кинематическими парами…………….....41 4.1. Задачи исследования; исходные данные; методы исследования...………….…41 4.2. Аналитический метод………………………………………………………….....42 4.3 Метод планов положений, скоростей и ускорений.…………………………...43 4.4.Метод кинематических диаграмм (метод графического дифференцирования)46 5. Кинетостатика механизмов. ……………………………………………….…….47 5.1. Расчёт сил инерции. ………………………………………………………….….47 5.2. Общие положения силового расчёта механизмов..………………………….…50 5.3. Метод планов сил для определения реакций в кинематических парах. ….….51 5.4. Определение уравновешивающей силы способом Н.Е.Жуковского.………....53 6. Динамика машин.…………………….…………………………………………...55 6.1. Вспомогательные задачи динамики машин.………………………….…………55 6.2. Характеристика режимов движения машин.………………………….………...57 6.3. Уравнения движения машин.……………………………….……………………59 6.4. Назначение и приближённое определение момента инерции маховика……...60
Предисловие Теория механизмов и машин (ТММ) излагает научные основы создания новых машин и механизмов, методы их построения и методы теоретического и экспериментального исследования. Из-за недостатка времени, отводимого на изучение этого курса в настоящее время, и требуемого объёма материала основное внимание данного пособия сосредоточено на необходимых понятиях механики машин (другое название дисциплины) и методах теоретического исследования механизмов и машин. Основой данного конспекта является курс, который автор читал в течение многих лет на различных факультетах ОмГТУ. Основной целью преподавания курса ТММ в настоящее время автор считает дать минимально необходимый объём знаний по механике машин для того, чтобы студент - машиностроитель понимал и успешно усваивал материал специальных предметов, которые ему придётся изучать на последующих курсах университета. К сожалению, из-за вышеуказанных причин в данном конспекте мало затрагиваются разделы, посвящённые проблемам синтеза механизмов, однако автор надеется, что студент, прочитав и усвоив содержание предлагаемого материала, сумеет в случае необходимости с привлечением других источников справиться с решением возникших перед ним задач проектирования механизмов. Для упорядочения изложения материал разбит на разделы, пронумерованные арабскими цифрами. Внутри разделов имеются более мелкие рубрики (параграфы), которые имеют двойную нумерацию – первая цифра обозначает номер раздела, а вторая – номер рубрики внутри раздела. Внутри этих рубрик могут быть ещё более мелкие подразделения. Такого порядка автор придерживается и при чтении курса. В конце каждого раздела приводится перечень вопросов для самопроверки. Это должно помочь студенту проверить, насколько глубоко он усвоил материал, и не требуется ли его повторить, а может быть и не один раз. В случае стойкого непонимания каких-либо моментов студент может обратиться за консультацией к преподавателю. В заключение автор выражает искреннюю благодарность студентке Любимцевой М.В., предоставившей ему свои записи лекций, и техническую помощь при оформлении материала.
Введение Теория механизмов и машин (ТММ) изучает общие методы исследования и проектирования механизмов и машин. Проблемы, которыми занимается ТММ, – это проблемы анализа и синтеза механизмов и машин. Анализ заключается в определении свойств существующих механизмов и машин. Это прямая задача механики машин. Обратная задача – синтез механизмов, т. е. создание новых механизмов, которые должны обладать улучшенными свойствами по сравнению с существующими с точки зрения производительности, надежности, долговечности и др. Вопросы для самопроверки 1. Для чего применяются зубчатые механизмы? 2. Что такое передаточное отношение? 3. Какие зубчатые механизмы называют редукторами, мультипликаторами? 4. Как можно выразить передаточное отношение в паре зубчатых колёс? 5. Изобразите схему рядового, ступенчатого соединений зубчатых колёс. 5. Какая связь между передаточным отношением сложного зубчатого механизма и передаточными отношениями отдельных его ступеней? 6. Как определяется передаточное отношение в механизмах с рядовым и ступенчатым соединениями колёс? 7. Какие зубчатые механизмы являются механизмами планетарного типа (эпициклическими)? 8. В чём состоит основное достоинство механизмов планетарного типа? 9. Назовите элементы типовой схемы механизма планетарного типа. 10. Для чего и как применяется метод обращения движения? 11. Каковы особенности аналитического расчета механизмов планетарного типа различных схем? 12. На чём основан графический метод исследования кинематики зубчатых механизмов? 13. Какова особенность графического расчёта кинематики дифференциального механизма с замкнутым контуром?
Основной закон зацепления Этот закон устанавливает связь между геометрией профилей зубьев и условиями передачи движения в зубчатом зацеплении (в более широком смысле – между геометрией элементов высшей пары и условиями передачи движения в механизме с высшей парой).
Свяжем с центроидами профили Пр1 и Пр2 так, чтобы они касались друг друга в точке К. Относительная скорость точки К1 профиля Пр1 по отношению к совпадающей с ней точке К2 профиля Пр2, (в данный момент обе точки находятся на нормали n–n в точке K) обозначена на рис.3.1 как V отн. Докажем следующие два положения: 1). Вектор 2) Вектор Доказанные положения позволяют сделать следующий вывод. Нормаль к профилям, проведённая в точке их касания, пересекает линию центров колёс в точке, совпадающей с полюсом зацепления, и таким образом делит межосевое расстояние центроид колёс на отрезки, обратно пропорциональные их угловым скоростям,
Другими словами, для правильной передачи движения с помощью высшей кинематической пары необходимо обеспечивать такую форму профилей зубьев, при которой нормаль к ним в точке контакта (контактная нормаль) проходила бы через полюс зацепления. Из этих рассуждений следует также, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали с межосевой линией. Профили, подчиняющиеся основному закону зацепления, называются сопряжёнными. Следствие 1. Если полюс П занимает неизменное положение на линии центров колёс, то передаточное отношение постоянно, и радиусы центроид также постоянны. Это соответствует круглым зубчатым колёсам. В противном случае колёса некруглые. Следствие 2. Если полюс П находится между центрами колёс, то они вращаются в противоположные стороны (внешнее зацепление колёс), и передаточное отношение имеет отрицательный знак. Следствие 3. Если полюс П находится вне отрезка О1О2, (выше или ниже этих центров), то колёса вращаются в одну сторону (внутреннее зацепление колёс). Следствие 4. Относительная скорость в точке касания профилей по существу является скоростью скольжения профилей зубьев. Чем дальше от полюса находится точка касания профилей, тем больше в ней скорость скольжения. Если в процессе передачи движения точка контакта профилей совпадёт с полюсом, то в этот момент скорость скольжения будет равна нулю. Существует большое количество профилей зубьев, удовлетворяющих этому закону. При выборе формы профилей руководствуются их технологичностью (простотой изготовления), простотой инструмента и расчетов. Этим требованиям в полной мере отвечает эвольвентное зацепление. Свойства эвольвенты 1) Нормаль к эвольвенте является касательной к основной окружности. 2) Центры кривизны эвольвенты лежат на основной окружности, так что основная окружность представляет собой эволюту, т. е. геометрическое место центров кривизны эвольвенты.
4) Радиус кривизны эвольвенты в данной точке равен дуге основной окружности, заключённой между точкой начала эвольвенты и точкой касания этой прямой с основной окружностью, ρA = 5) Правая и левая ветви эвольвенты симметричны. 6) Все точки эвольвенты лежат снаружи от основной окружности.
Уравнение эвольвенты Для получения уравнения эвольвенты обратимся к рис. 3.3. Положение произвольной точки Ay эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиус-вектора OA0 (или OC0):
Для определения полярного угла θ y сначала выразим длину дуги основной окружности через её радиус и центральный угол:
Выразим теперь противолежащий углу αy катет AyCy в ∆OAyCy:
На основании четвёртого свойства эвольвенты имеем
Подставляя в это равенство соответствующие выражения и решая его относительно θ y, получаем
В этих математических выражениях и на рис. 3.3 угол αy называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, т. е. inv, так что окончательно уравнение имеет вид: θy = invαy. В математических справочниках приводятся таблицы эвольвентной функции, в которых аргумент αy изменяется от нуля до нескольких десятков градусов.
Элементы зубчатого колеса Здесь рассматриваются те элементы колеса, которые относятся к его ободу, где располагаются зубья (рис. 3.4). Шаг колеса p – это расстояние по делительной окружности между одноимёнными профилями двух соседних зубьев, p = π·m. Шаг включает два параметра – толщину зуба s и ширину впадины e. Если s = e, то имеем колесо с равноделённым шагом, в противном случае имеем колесо с неравноделённым шагом. Делительная окружность (её радиус – делит зуб на головку и ножку; – модуль m на этой окружности имеет стандартное значение; – радиус окружности имеет величину r = 0,5m – в точке на делительной окружности профильный угол эвольвенты αy = 20º и обозначается буквой α без индекса. Основная окружность является базовой для образования эвольвенты (от неё начинается эвольвентная часть зуба). Радиус этой окружности получается из рассмотрения прямоугольного треугольника с углом при вершине O, равным α, и одним из катетов, равным Окружность вершин является габаритной окружностью колеса, её радиус определяется формулой
где Диаметр окружности вершин является диаметром заготовки для изготовления зубчатого колеса. Окружность впадин ограничивает зуб у основания, её радиус равен
Контур зуба от основной окружности до окружности вершин очерчен эвольвентой, которая сопрягается с окружностью впадин переходной кривой (эквидистантой удлинённой эвольвенты). Свойства зацепления 1) Передаточное отношение постоянно в любой фазе зацепления, так как оно может быть выражено через радиусы основных окружностей. Для доказательства используем подобные прямоугольные треугольники (рис. 3.5)
2) Передаточное отношение не зависит от изменения межосевого расстояния 3) Правильное зацепление эвольвентных профилей происходит только в пределах линии зацепления N1N2, так как только в этих пределах контактирующие эвольвентные профили имеют общую нормаль. 4) Эвольвентные колёса одного модуля имеют полную взаимозаменяемость, т. е. могут составить правильное зацепление.
Методы изготовления
Метод копирования заключается в том, что профиль зуба колеса повторяет форму профиля инструмента (рис. 3.6), который, в свою очередь, теоретически точно соответствует форме эвольвенты и переходной кривой зуба конкретного колеса. Инструментом могут служить дисковая или пальцевая модульные фрезы, или протяжка. Достоинством метода является возможность применения универсального обоудования (горизонтально- или вертикально-фрезерных станков), оснащенного делительной головкой для точного поворота заготовки на угловой шаг после обработки очередной впадины. Такое оборудование имеется, как правило, в ремонтной службе любого предприятия. К недостаткам следует отнести низкую точность и невысокую производительность. Кроме того, геометрия эвольвенты полностью определяется радиусом основной окружности, зависящей от модуля и числа зубьев, поэтому каждое колесо по существу должно иметь собственный инструмент для нарезания зубьев. Так как это невозможно, то применяют наборы фрез одного модуля из 8 или 15 штук. Каждая фреза набора используется для изготовления нескольких колёс с разными числами зубьев, одному из которых она обеспечивает номинально точную эвольвенту, а другие получают ошибку профиля. Ошибка получается тем больше, чем больше отклоняется число зубьев колеса от номинала. Метод обкатки (огибания) состоит в том, что профиль зуба колеса получается как огибающая ряда последовательных положений профиля инструмента (рис. 3.7).
С точки зрения кинематики движение инструмента относительно ещё ненарезанного колеса с помощью специальной цепи деления станка повторяет то движение, которое осуществляется в зубчатой передаче. Так как инструмент, по существу представляет собой зубчатое колесо с геометрией режущего инструмента, то в процессе нарезания он срезает всё, что попадает в зону движения режущих кромок, а оставшееся и представляет собой зубья колеса. Метод характеризуется высокой точностью, производительностью и, что немаловажно, позволяет инструментом одного модуля изготавливать зубчатые колёса с любым числом зубьев. К недостаткам метода можно отнести необходимость в специальном зубообрабатывающем оборудовании, однако этот недостаток с лихвой компенсируется достоинствами метода.
Зацепления Коэффициент перекрытия Коэффициентом перекрытия называется отношение длины активной линии зацепления к основному шагу зубчатого колеса, он обозначается
Передача движения в зубчатом зацеплении происходит таким образом, что, прежде чем предыдущая пара зубьев выйдет из зацепления (из контакта), последующая должна войти в зацепление (в контакт). Чем раньше она вступит в зацепление, тем более плавно работает передача. Количественной характеристикой этого качества и является коэффициент перекрытия, т. е. он, по существу, характеризует плавность работы зубчатой передачи. Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной активной лини зацепления и основным шагом показано на рис. 3.12. Точка контакта профилей зубьев перемещается вдоль активной линии зацепления от точки H1 к точке H2. Основной шаг короче активной линии зацепления, поэтому в пределах этой линии работают то одна, то две пары зубьев. Если отложить, как показано на рис. 3.12, основной шаг pb от точек H1 и H2, то отрезок H1H2 будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее. Удельное скольжение Удельным скольжением называется отношение скорости скольжения профилей в точке их касания к скорости перемещения точки касания по профилю. Этот показатель характеризует износ зубьев в результате трения скольжения их боковых (рабочих) поверхностей. Возьмём точки К1 первого профиля и К2 второго профиля, Согласно определению, удельное скольжение выразится двумя математическими выражениями, относящимися к разным колёсам:
Для определения тангенциальных составляющих скоростей обратимся к рис. 3.14. Соединим точку К1 с центром О1 вращения колеса 1 радиусом R1, и точку К2, совпадающую с точкой К1, с центром О2 радиусом R2. Перпендикулярно радиусу R1 в сторону вращения колеса 1 отложим абсолютную скорость точки К1, равную ками преобразований
В этих выражениях буквой К обозначены совпадающие друг с другом точки К1 и К2. Схематический график удельного скольжения показан на рис. 3.15.
Угол зацепления Формулу для определения угла зацепления приведём здесь без вывода из-за его громоздкости
Из этой формулы, в частности, видно, что в нулевой передаче Радиусы окружностей впадин При образовании нулевого колеса его центроидой, как всегда, является делительная окружность (рис.3.18), а центроидой инструмента служит его делительная прямая (на рисунке профиль инструмента и его делительная прямая и прямая вершин показаны тонкими линиями). Поэтому радиус
На рис. 3.18 расположение инструмента по отношению к нарезаемому колесу изображено жирными линиями.
Радиусы окружностей вершин Расчёт радиусов окружностей вершин понятен из рис. 3.19, где представлены те элементы зацепления, которые связаны с этим расчётом. Непосредственно из рисунка видно, что радиус окружности вершин первого колеса равен
радиус окружности вершин второго колеса равен
Вопросы для самопроверки 1. В чём заключается существо основного закона зацепления? 2. Какие профили зубьев колёс называются сопряжёнными? 3. Что такое эвольвента окружности, производящая прямая? 4. Какими свойствами обладает эвольвента окружности? 5. Что такое эвольвентная функция? 6. Назовите элементы зубчатого колеса, какими линиями очерчивается про- филь зуба? 7. Что называется шагом колеса, модулем, головкой, ножкой зуба? 8. В каком месте измеряется толщина зуба, ширина впадины колеса? 9. Какими свойствами обладает делительная окружность? 10. Что такое коэффициент высоты головки зуба, чему он равен? 11. Какая окружность колеса называется основной? 12. Назовите элементы зацепления пары колёс. 13. Что такое полюс зацепления? 14. Какие окружности колёс называются начальными? 15. Что такое угол зацепления? 16. Что такое линия зацепления, активная линия зацепления? 17. Что такое радиальный зазор, за счёт чего он образуется? 18. Сформулируйте свойства эвольвентного зацепления. 19. Какими методами изготавливают эвольвентные зубья, в чём заключается существо методов? Каковы основные достоинства и недостатки методов? 20. Что такое реечный производящий исходный контур(инструментальная рейка)? 21. Что такое подрез зубчатого колеса? 22. Какое число зубьев считается минимальным, от чего оно зависит? 23. Как предотвратить подрез зубчатого колеса? 24. Что такое коэффициент смещения исходного контура? 25. Какие зубчатые колёса называются нулевыми, положительными и отрицательными? 26. Назовите качественные характеристики эвольвентногозацепления. 27. Что называется коэффициентом перекрытия, и что он характеризует? 28. Что такое удельное скольжение, почему возникает скольжение в контакте зубьев? 29. Почему в полюсе зацепления удельное скольжение равно нулю? 30. Что такое коэффициент удельного давления, где он применяется? 31. Для чего назначаются коэффициенты смещения при нарезании зубчатых колёс? 32. Как определяются геометрические размеры зубчатых колёс: угол зацепления, радиусы начальных окружностей, межосевое расстояние, радиусы окружностей впадин, радиусы окружностей вершин и толщина зуба по делительной окружности?
Задачи исследования 1)Определение положений звеньев механизма и определение траекторий отдельных его точек. 2)Определение линейных скоростей точек механизма и угловых скоростей его звеньев. 3)Определение линейных ускорений точек механизма и угловых ускорений его звеньев. Исходные данные Для решения задач кинематики необходимо иметь 1)Кинематическую схему механизма и все кинематические размеры его звеньев. 2)Закон движения входного (ведущего) звена. Методы исследования 1)Аналитический. 2)Графо-аналитический (метод планов положений,скоростей и ускорений). 3)Метод графического дифференцирования. 4)Экспериментальный. Аналитический метод Метод заключается в определении математических выражений, Для составления некоторого первоначального представления о методе рассмотрим кинематику синусного механизма (рис. 4.1). Механизм состоит из кривошипа 1, вращающегося вокруг неподвижной точки О, конец А которого образует вращательную кинематическую пару с ползуном 2. Ползун движется по вертикальному элементу ведомого звена 3, которое движется вдоль неподвижных гоизонтальных направляющих. На первом этапе определяется зависимость перемещения S ведомого звена от угла α1 поворота ведущего кривошипа 1. Из рис. 4.1 видно, что
Дифференцируя по
дифференцируя во второй раз, получаем аналог ускорения ведомого звена
З а м е ч а н и е. Следует обратить внимание на то, что зависимость
4.3. Метод планов положений, скоростей и ускорений Вопросы для самопроверки 1. Сформулируйте задачи кинематического анализа механизмов с низшими парами. 2. Перечислите методы исследования кинематики механизмов. 3. Что должно быть задано для исследования кинематики механизма? 4. В чём заключается сущность аналитического метода исследования кинематики? 5. Что называется масштабом в ТММ? 6. Что такое разметка механизма? 7. Для чего строится разметка? 8. Как определяются скорость и ускорение конца кривошипа? 9. Запишите векторные уравнения для построения планов скоростей и ускорений и объясните их составляющие. Какое правило механики положено в основу этих уравнений? 10. Как определяются скорости и ускорения центра масс шатуна? 11. Как определить угловые скорость и ускорение стержневого звена? 12. Какое правило математики положено в основу графического дифференцирования функции, заданной в виде графика? 13. Приведите пример построении графика производной при заданном графике функции. 14. Как определяются масштабы по осям
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.100 (0.011 с.) |

 Возьмём две центроиды Ц1 и Ц2, принадлежащие колёсам 1 и 2 (рис. 3.1). Эти центроиды касаются друг друга в точке П (прописная греческая буква «пи»), называемой полюсом зацепления.
Возьмём две центроиды Ц1 и Ц2, принадлежащие колёсам 1 и 2 (рис. 3.1). Эти центроиды касаются друг друга в точке П (прописная греческая буква «пи»), называемой полюсом зацепления.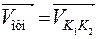 перпендикулярен нормали, в противном случае появится составляющая относительной скорости, направленная вдоль неё. Если эта составляющая будет направлена в сторону Пр2, то произойдёт внедрение профиля Пр1 в профиль Пр2, если она будет направлена в обратную сторону, то произойдёт отрыв профилей друг от друга. В обоих случаях высшая пара будет разрушена. Так что данное положение доказано.
перпендикулярен нормали, в противном случае появится составляющая относительной скорости, направленная вдоль неё. Если эта составляющая будет направлена в сторону Пр2, то произойдёт внедрение профиля Пр1 в профиль Пр2, если она будет направлена в обратную сторону, то произойдёт отрыв профилей друг от друга. В обоих случаях высшая пара будет разрушена. Так что данное положение доказано. перпендикулярен отрезку КП. Так как полюс П является мгновенным центром поворота центроиды Ц1 относительно центроиды Ц2, то, согласно положению теоретической механики, все точки, связанные с центроидой Ц1, имеют скорости, направленные перпендикулярно отрезку, соединяющему данную точку с центром (полюсом) поворота. Это и служит доказательством перпендикулярности вектора скорости и отрезка КП. Следует также отметить, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали профилей с линией центров колёс.
перпендикулярен отрезку КП. Так как полюс П является мгновенным центром поворота центроиды Ц1 относительно центроиды Ц2, то, согласно положению теоретической механики, все точки, связанные с центроидой Ц1, имеют скорости, направленные перпендикулярно отрезку, соединяющему данную точку с центром (полюсом) поворота. Это и служит доказательством перпендикулярности вектора скорости и отрезка КП. Следует также отметить, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали профилей с линией центров колёс. .
. 3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.
3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.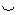 C0C.
C0C. длиной радиус-вектора R y и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
длиной радиус-вектора R y и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:



 .
. , в зацеплении двух колёс имеет индекс номера колеса):
, в зацеплении двух колёс имеет индекс номера колеса): ;
; ,
,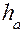 – высота головки зуба, причём
– высота головки зуба, причём  . Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.
. Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.  .
. ,
, где
где  – высота ножки зуба, определяемая равенством
– высота ножки зуба, определяемая равенством  , второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину
, второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину  .
. и
и 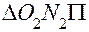 и запишем цепочку равенств:
и запишем цепочку равенств: .
. по той же причине, что и в предыдущем случае.
по той же причине, что и в предыдущем случае. зубчатых колёс
зубчатых колёс
 и определяется отношением
и определяется отношением
 .
. совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.
совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев. и
и  .
. , и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную
, и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную 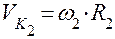 . Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости
. Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости 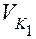 и
и 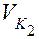 на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-
на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-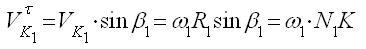

 C учётом этого ранее записанные выражения примут следующий вид:
C учётом этого ранее записанные выражения примут следующий вид: ,
,  .
.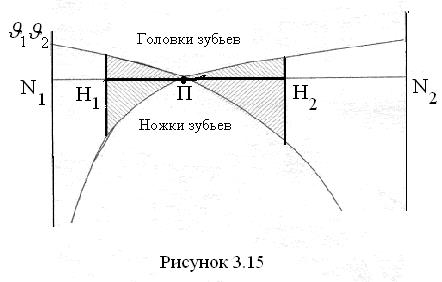 График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю. .
. угол зацепления
угол зацепления  равен углу профиля инструмента
равен углу профиля инструмента  , в положительной передаче
, в положительной передаче 
 , в отрицательной передаче всё наоборот, т.е.
, в отрицательной передаче всё наоборот, т.е. 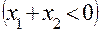 и соответственно
и соответственно 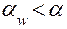 .
. окружности впадин нулевого колеса равен разности
окружности впадин нулевого колеса равен разности  . При смещении инструмента на величину
. При смещении инструмента на величину 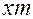 радиус окружности впадин увеличивается на эту же величину и приобретает значение
радиус окружности впадин увеличивается на эту же величину и приобретает значение
 .
.
 ,
, .
. описывающих функциональную связь между входными и выходными параметрами механизма. Для этого служат различные приёмы и методы, такие как метод векторных контуров, который образуется заменой кинематических размеров звеньев векторами, с последующим проецированием этого контура на оси системы координат и получением на этой основе соответствующих уравнений, описывающих кинематику данного механизма. Этой же цели служит метод разбиения схемы механизма на прямо- или косоугольные треугольники, решая которые, получают необходимые математические выражения.
описывающих функциональную связь между входными и выходными параметрами механизма. Для этого служат различные приёмы и методы, такие как метод векторных контуров, который образуется заменой кинематических размеров звеньев векторами, с последующим проецированием этого контура на оси системы координат и получением на этой основе соответствующих уравнений, описывающих кинематику данного механизма. Этой же цели служит метод разбиения схемы механизма на прямо- или косоугольные треугольники, решая которые, получают необходимые математические выражения. .
. ,
, .
. , отражающая закон преобразования движения в механизме, называется функцией положения механизма. Её первая производная по
, отражающая закон преобразования движения в механизме, называется функцией положения механизма. Её первая производная по  и выполнить дифференцирование по времени
и выполнить дифференцирование по времени  . Попутно обнаруживается и связь между кинематическими функциями и их аналогами.
. Попутно обнаруживается и связь между кинематическими функциями и их аналогами.


