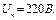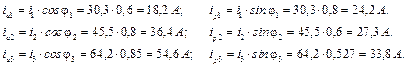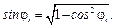Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до розв’язування задачСодержание книги
Поиск на нашем сайте
Задача №1
Розв’язування В електричному колі кількість віток p = 3, кількість вузлів (c та d) q = 2. Задаємось довільно напрямами струмів у вітках. Опори вітки cad R 1 та R 3 ввімкнені послідовно:
Опори вітки cbd R 2 та R 4 ввімкнені послідовно:
Вітки cad і cbd ввімкнені паралельно. Опір паралельних віток:
Еквівалентний опір кола:
Струм в нерозгалуженій частині кола:
Напруга між точками с і d:
або
Струми у вітках знаходимо за законом Ома:
Перевірка: (перший закон Кірхофа для вузла d)
Для визначення напруги U ab за другим законом Кірхгофа для контуру сdв (обхід за годинниковою стрілкою) складаємо рівняння для визначення напруги U ab.
Баланс потужностей (потужність джерела дорівнює потужності приймача):
Задача №2 В електричному колі, зображеному на рис. 8, відомі ЕРС джерел і опори резисторів. Визначити струми у всіх вітках кола і режим роботи кожного із джерел. Скласти баланс потужностей. Задачу вирішити двома методами: 1) застосування законів Кірхгофа і 2) вузлової напруги. Дано: Е 1 = 140 В, Е 2 = 150 В, Е 3 = 160 В, R 1 = 5 Ом, R 2 = 1 Ом, R 3 = 4 Ом, R 4 = 2 Ом.
Розв’язування В електричному колі чотири вітки p = 4, два вузли q = 2, три контури n = p – (q– 1) = 4 – 1 = 3. а) задаємось довільними напрямами струмів у вітках та обходом контурів. Складаємо за першим та другим законами Кірхгофа рівняння для вузла а і контурів І, ІІ, ІІІ.
Систему лінійних алгебраїчних рівнянь можна розв’язати одним з багатьох методів: методом Гаусса, методом виключення змінних, методом Крамера та ін. Розв’яжемо її методом Крамера (визначників). Значення опорів у стовпцях відповідають відповідно струмам
Струми віток:
б) Вибираємо напрям вузлової напруги від вузла а до вузла б. Провідності віток:
Міжвузлова напруга:
де
Струми віток знаходимо за другим законом Кірхгофа: Для першої вітки:
Для другої вітки:
Для третьої вітки:
Для четвертої вітки:
Як видно з розрахунків результати за обома методами однакові. Так, як реальні напрями струмів і 1, і 2, і 3 у вітках співпадають з відповідними ЕРС, то вітки працюють в режимі віддачі електроенергії або в режимі генераторів. Струм у четвертій вітці протікає в протилежному напрямі. Складаємо баланс потужностей (потужність, що віддається дже-релом дорівнює потужності приймачів):
Задача №3 У коло синусоїдного струму з частотою f = 50 Гц (рис. 9) ввім-кнені послідовно дві котушки і конденсатор. Визначити струм, напруги на окремих елементах кола, скласти баланс потужностей, якщо відомі напруга на вході і параметри елементів. Визначити резонансну частоту. Побудувати векторну діаграму.
Рис. 9. Схема електричного кола Дано: Розв’язування Знаходимо опори елементів: Реактивні (індуктивні):
Реактивний (ємнісний):
Комплексний повний опір кола в алгебраїчній формі:
або в показниковій формі де
Комплексний струм кола: Спадки напруг на елементах кола:
Реактивні потужності:
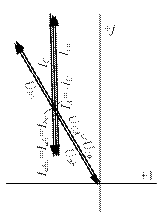
Рис. 10. Векторна діаграма напруг і струму Резонансна частота:
Задача 4 У коло синусоїдного струму (рис. 11) з частотою f = 50 Гц ввім-кнені через резистор R 0 дві паралельні вітки. Параметри елементів і напруга на вході відомі. Знайти струми у вітках і нерозгалуженій частині кола. Визначити зсуви фаз всього кола і в обох вітках. Скласти баланс потужностей, побудувати векторну діаграму.
Рис. 11 Схема електричного кола Дано: Розв’язування Знаходимо реактивні опори елементів у вітках: Індуктивний: Ємнісний: Комплексні повні опори віток кола:
де
де
Еквівалентний опір паралельних віток кола:
Загальний опір кола:
Комплекс струму в нерозгалуженій частині кола:
Спадок напруги на опорі R 0: Напруга паралельних віток: Струми у вітках:
Баланс потужностей: Рдж = Рпр.
Векторна діаграма зображена на рис. 12. mu = 20 В/см, mi = 5 А/см.
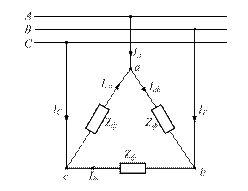
Рис. 12. Векторна діаграма напруг і струмів Задача 5 До трифазної лінії (рис. 13) з лінійною напругою підключений симетричний трифазний приймач, з’єднаний за схемою „зірка”. Опори кожної з фаз приймача рівні Zф = Rф+jX.
Рис. 13. Схема електричного кола Визначити струм у фазах приймача та в нульовому провіднику, також споживану приймачем активну потужність в наступних режимах: а) в симетричному трьохфазному; б) при обриві однієї фази приймача; в) при обриві нульового провідника при обірваній фазі. Побудувати для всіх трьох випадків топографічні діаграми напруг і на них показати вектори струмів. Дано: Розв’язування а) Симетричне навантаження: При з’єднанні «зірка» фазні напруги в
Розрахунок струмів проводимо комплексним методом. Вектор напруги
Комплексні лінійні напруги визначаємо за другим законом Кірх-гофа як геометричну різницю фазних напруг, а саме:
Модуль повного опору фаз приймача рівний:
Кут зсуву фаз кожної вітки між струмом, що протікає у вітці та напругою, що до неї прикладена рівний:
Комплексний повний опір: Визначаємо фазні струми віток і струм нейтралі:
У симетричному режимі струм у нульовому провіднику відсутній. Потужність приймача: б) Обрив фази с (ключ K 1 розімкнений): При обриві фази струм у фазі с дорівнює нулю. Фазні струми:
Струм у нейтральному провіднику
Активна потужність: в) обрив фази с і нейтрального провідника (ключі K 1 і K 2 розімкнені): При обриві фази с та нульового провідника трифазне коло перет-ворюється в однофазне із послідовним з’єднанням фаз а і b. Напруги Uфа та Uфb однакові за величиною і дорівнюють половині лінійної напруги UAB.
Фазні струми:
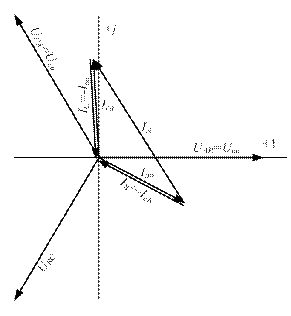
Активна потужність: Задавшись масштабами напруг та струмів будуємо векторні діа-грами для трьох випадків (рис.14, 15, 16): m u = 50 В/см, m i = 2 А/см.
Рис. 14. Векторна діаграма для режиму а.
Рис. 15. Векторна діаграма для режиму б.
Рис. 16. Векторна діаграма для режиму в. Задача 6 До трифазної лінії з лінійною напругою підключений симетрич-ний трифазний приймач (рис. 17.), з’єднаний за схемою „трикутник”. Опори кожної з фаз приймача рівні Zф = Rф + jXф. Визначити струм в фазах приймача та в лінійних провідниках, а також споживану приймачем активну потужність в наступних режимах: а) в симетричному трьохфазному; б) при обриві однієї фази приймача; в) при обриві лінійного провідника. Побудувати для всіх трьох випадків топографічні діаграми напруг і на них показати вектори струмів. Для симетричного трифазного режиму визначити реактивну потужність і ємність батареї конденсаторів в мкФ, необхідну для збільшення коефіцієнту потужності до величини: а) cos φ = = 0,95, б) cos φ = 1.
Рис. 17. Схема електричного кола Дано: Розв’язок а) Симетричне навантаження: При такому з’єднанні лінійні напруги рівні фазним, тобто
Розрахунок струмів проводимо комплексним методом. Вектор лі-нійної напруги Відповідно комплекси векторів напруг
Модуль повного опору фаз приймача рівний:
Кут зсуву фаз кожної вітки між струмом, що протікає у вітці та напругою, що до неї прикладена рівний:
Комплексний повний опір:
Визначаємо фазні струми віток:
Лінійні струми:
Потужність трифазного приймача:
Визначаємо реактивну потужність та ємність батареї конденсато-рів, що необхідні для збільшення
де При
При
б) Обрив фази в (bс):
При обриві фази зірка лінійних напруг залишається без змін. Фазні струми:
Знаходимо лінійні струми.
Активна потужність:
в) обрив лінії В:
При обриві лінійного провідника В трифазне коло перетворюєть-ся у звичайне однофазне із змішаним з’єднанням приймачів (послідовно з’єднані фази а і b приєднані до фази с). Приймач фази с знаходиться як і раніше під лінійною напругою UCA, а напруги на інших двох фазах в два рази менші за напругу UCA. Фазні струми:
Лінійні струми:
Активна потужність:
Задавшись масштабами напруг і струмів будуємо векторні діаграми для трьох випадків.
Рис. 18. Векторна діаграма для режиму а
Рис. 19. Векторна діаграма для режиму б
Рис. 20. Векторна діаграма для режиму в Задача 7 Розрахувати магніторушійну силу (МРС) та струм котушки електромагніту, що забезпечує створення тягового зусилля Q 1. Крива намагнічування (залежність В = f (Н)) магнітопроводу задана.
Рис. 21. Схема електромагніту Дано: с = 60 мм, δ = 2,0 мм, Q 1 = 5500 H, W = 2100.
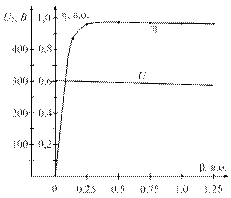
Розв’язування Будуємо характеристику намагнічування.
Рис. 22. Крива намагнічування магнітопроводу B = f (H) З формули
де Розділивши магнітне коло на однорідні ділянки знаходимо довжи-ни їх середніх магнітних ліній
Площі поперечного перерізу всіх ділянок однакові:
Магнітний потік і магнітна індукція в повітряному проміжку:
З кривої намагнічування за значенням магнітної індукції В знахо-димо напруженість магнітного поля в магнітопроводі: Н 1 = H 2 = 1960 А/м. Напруженість магнітного поля в повітряному зазорі:
Магніторушійну силу котушки визначаємо за законом повного струму:
Струм котушки, що забезпечує тягове зусилля Q 1
Задача 8 Розрахувати обмотку підковоподібного електромагніту з силою тяги
Рис. 23. Магнітопровід електромагніту
Розв’язування Магнітну індукцію визначаємо за формулою:
За кривою намагнічування визначаємо величину напруженості маг-нітного поля в сталі Напруженість магнітного поля в немагнітному проміжку дорівнює:
Визначаємо середню лінію протікання магнітного потоку:
За законом повного струму визначаємо намагнічуючу силу:
За формулою опору довжина провідника дорівнює:
з урахуванням що Висота котушки h приблизно дорівнює 80% висоти вікна електро-магніту, тобто,
Відстань від сердечника до витків внутрішнього (першого) шару, внаслідок використання каркасу та ізолюючих прокладок, нехай дорівнює 4 мм. Припустимо також, що товщина котушки D разом з каркасом складає також 80% ширини вікна електромагніту
Отже, переріз провідників котушки (односторонній) дорівнює:
Перевіримо чи вкладуться всі провідники котушки в заданій площі. Діаметр ізольованого провідника d 1 в k разів більший за діаметр провідника d без ізоляції. Для провідника марки ПЕВ–1 або ПЕВ–2 (емалеве покриття) k = 1,5. Припустимо, що в поперечному перерізі котушки кожен виток зай-має квадрат із стороною d 1 = d·k, запишемо:
звідси
Представимо намагнічуючу силу у вигляді:
де З останньої формули визначимо необхідну товщину котушки:
Отже, необхідна товщина котушки Довжина середнього витка котушки дорівнює:
де Число витків визначаємо за формулою:
Струм в обмотці:
Площа поперечного перерізу провідника дорівнює:
Із довідника вибираємо провідник відповідного діаметру так, щоб його площа була найближчою до площі Задача 9 Однофазний трансформатор має такі номінальні параметри: Розв’язування Визначаємо коефіцієнт трансформації: Номінальний струм первинної обмотки: Струм неробочого ходу визначаємо за формулою:
Визначаємо параметри заступної схеми. Опори вітки намагнічування знаходимо з досліду холостого ходу:
Напруга короткого замикання: Опори короткого замикання, активні і реактивні опори первинної і вторинної обмоток:
Для визначення вторинної напруги і струму під час навантаження визначимо коефіцієнт завантаження
де
активна складова опору навантаження,
реактивна складова опору навантаження.
Зміна вторинної напруги:
де
активна складова напруги короткого замикання,
реактивна складова напруги короткого замикання. Визначаємо вторинні напругу та струм:
Задача 10 Трифазний трансформатор характеризується наступними вели-чинами: номінальна потужність S ном, номінальна максимальна лінійна напруга U 1ном, номінальна мінімальна напруга U 2ном, процентне значення напруги короткого замикання u к %, процентне значення струму холостого ходу i 0 %, потужність втрат холостого ходу P 0 (при первинній напрузі, рівній номінальній), потужність втрат короткого замикання P к (при струмах в обмотках, рівних номінальним), група з’єднання обмоток.
Визначити: а) коефіцієнт трансформації; б) фазні напруги первин-ної і вторинної обмоток при холостому ході; в) номінальні точки в обмот-ках трансформатора; г) параметри Т -подібної схеми заміщення R 0, Х 0, R 1, Х 1, R 2, Х 2; д) вторинну напругу при cos φ2 = 0,8 і значеннях коефіцієнта навантаження β: 0,25; 0,5; 0,75; 1,0; 1,25; е) ККД трансформатора при тих самих значеннях cos φ2 і коефіцієнта навантаження при умові, що транс-форматор знаходиться під навантаженням протягом року Т годин, а в інший час коло вторинної обмотки розімкнуте. Побудувати залежності U 2 = f (β) і η = f (β), включаючи точку β = 0. Вказівки. 1. Прийняти, що в досліді холостого ходу опір первинної обмотки малий в порівнянні з опором вітки намагнічення кола. 2. Прийняв-ти, що в досліді короткого замикання потужність втрат ділиться порівну між первинною і вторинною обмотками (R 1 = R 2 = R к/2, Х 1 = Х 2 = Х к/2). Дано: Розв’язування а) Для з’єднання Y/Y -0 лінійний та фазний коефіцієнти транс-формації однакові
б) фазні напруги первинної та вторинної обмоток:
в) номінальні струми в обмотках трансформатора:
г) параметри Т -подібної схеми заміщення. Повний, активний та реактивний опори фази при короткому замиканні:
Опори первинної обмотки:
Опори вторинної обмотки трансформатора:
Струм холостого ходу: Опори намагнічуючої вітки:
Вторинна напруга при
Задаючись значеннями коефіцієнта навантаження β за формулами: Результати заносимо в таблицю і будуємо залежності U 2 = f (β) і η = f (β).
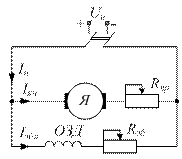
Рис. 26. Залежності U 2 = f (β) і η = f (β). Задача 11 Електродвигун постійного струму з паралельним збудженням ха-рактеризується наступними номінальними даними: потужність P ном, на-пруга на затискачах U ном, частота обертання n ном, ККД η, втрати потуж-ності в колі якоря Р я% і в колі збудження Р зб % задані в процентах від споживаної потужності P 1ном. Визначити: а) струм у колі збудження I зб.ном; б) струм якоря I я.ном; в) струм, що споживається двигуном I ном; г) номі-нальний момент М ном; д) пусковий обертовий момент і опір пускового реостату при I я.п = 2· I я.ном. Побудувати природну і штучну механічні хара-ктеристики двигуна при опорі в колі якоря R я.р. = 3· R я. Дано: P ном = 14 кВт, U ном = 220 В, Р я = 4 %, Р зб = 4,6 %, n ном = 2400 об/хв., η = 0,84. Розв’язок Електрична схема двигуна:
Рис. 27. Електрична схема двигуна
а) електрична потужність, що споживається двигуном:
б) номінальний струм обмотки збудження:
в) номінальний струм двигуна: г) номінальний струм якоря: д) номінальний момент двигуна:
е) пусковий момент двигуна: є) опір обмотки якоря: Опір пускового реостату:
ж) побудова механічних характеристик: номінальна кутова швидкість обертання якоря:
Конструктивний коефіцієнт двигуна:
Кутова швидкість холостого ходу:
Штучна характеристика:
Пускова характеристика:
Будуємо механічні характеристики двигуна:
Рис. 28. Механічні характристики двигуна постійного струму Задача 12 Трифазний асинхронний двигун загального призначення серії 4А ввімкнений в мережу з напругою 220/380 В. Визначити: а) схему з’єднан-ня обмоток статора; б) синхронну частоту обертання n 0; в) обертальні мо-менти двигуна, номінальний М ном, пусковий М п, критичний М к, г) потуж-ність, використану двигуном P 1ном; д) номінальний Iном і пусковий I п струми в статорі двигуна; е) критичне ковзання S к; ж) пусковий обертовий момент у випадку пуску при напрузі, рівній 90% від номінальної; з) обертальний момент для ряду ковзання S = S ном; Sк; 0,2; 0,4; 0,6; 0,8; 1,0. Побудувати графік M = f (S). Дано: P н = 4000 Вт, U 1ф = 380 В, n ном = 720 об/хв, ηном = 0,83, cos φном = 0,7, K I = I п/ I ном = 5,5, K п = М п/ M ном = 1,9, K м = = М max/ М ном = 2,6. Розв’язування Обмотки статора з’єднані зіркою. Синхронна частота обертання магнітного поля статора приймає-ться з ряду: 3000 об/хв, 1500 об/хв, 1000 об/хв, 750 об/хв, 500 об/хв, причому найближча найбільша. Номінальний момент двигуна:
Максимальний момент двигуна:
Пусковий момент двигуна: Електромагнітна потужність двигуна:
Струм статора: Пусковий струм статора: Номінальне ковзання двигуна: Критичне ковзання двигуна:
Як відомо момент пропорційний напрузі в квадраті. Напруга понизилась на 10% (тобто стало 0,9 U1Ф). 0,92 = 0,81. Тобто, пусковий момент зменшився на 19 % (1 - 0,81 = 0,19).
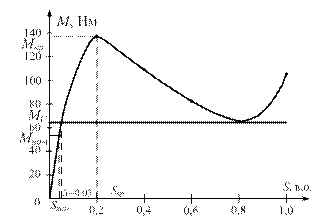
Для побудови механічної характеристики використовуємо форму-лу Клосса, попередньо задавшись значеннями ковзання.
Результати заносимо в таблицю і будуємо графік.
Частоту обертання при заданому моменті навантаження знаходи-мо з механічної характеристики М = f (s).
Рис. 29. Механічна характеристика асинхронного двигуна М = f (s) Для значення М С = 63,6 Нм ковзання становить s = 0,05. Частота обертання валу становить:
Задача 13 Визначити переріз мідних провідників лінії однофазного змін-ного струму при умові, щоб втрата потужності не перевищувала
Рис. 30. Схема електричного кола Розв’язування Струми приймачів:
Активні та реактивні складові струмів приймачів
Тут Активна та реактивна складові струму на ділянці Аа:
Струм, на ділянці Аа: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

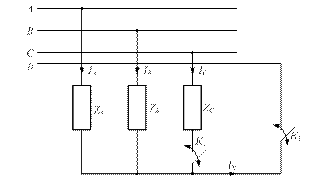
 Дано: Е = 25 В, R 1 = 10 Ом, R 2= 10 Ом, R 3= 2 Ом,
R 4= 3 Ом, R 5= 5 Ом, R 6= 0 Ом.
Дано: Е = 25 В, R 1 = 10 Ом, R 2= 10 Ом, R 3= 2 Ом,
R 4= 3 Ом, R 5= 5 Ом, R 6= 0 Ом.



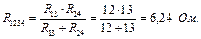
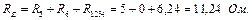

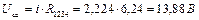


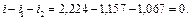



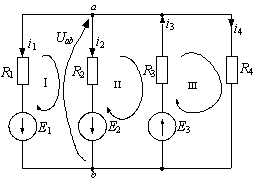


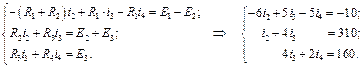

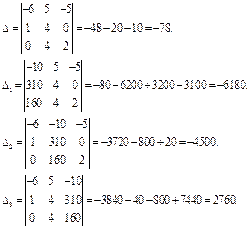
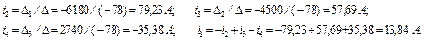


 входять зі знаком «–», так як ЕРС Е 1, Е 2 напрямлені проти вузлової напруги.
входять зі знаком «–», так як ЕРС Е 1, Е 2 напрямлені проти вузлової напруги.
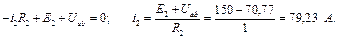

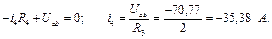
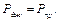
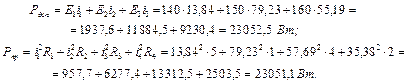

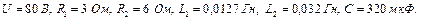

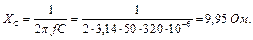
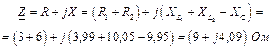
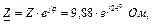

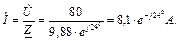
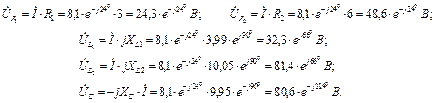 Баланс потужностей. Активні потужності: Рдж= Рпр.
Баланс потужностей. Активні потужності: Рдж= Рпр.
 Векторну діаграму напруг і струму зображено на рис. 10. Масштаб: mu = 10 В/см, mi = 2 A/см.
Векторну діаграму напруг і струму зображено на рис. 10. Масштаб: mu = 10 В/см, mi = 2 A/см.
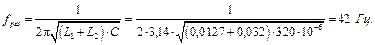

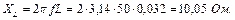
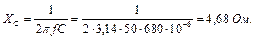
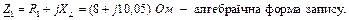

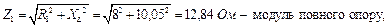


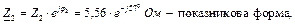
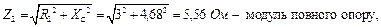







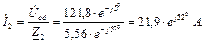
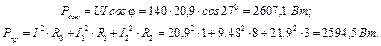


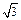 разів менші за лінійні
разів менші за лінійні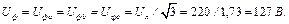
 напрямлений вздовж дійсної осі
напрямлений вздовж дійсної осі 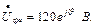
 Відповідно вектори напруг
Відповідно вектори напруг 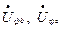 зсунуті на кути -1200 і 1200 (-2400), тобто:
зсунуті на кути -1200 і 1200 (-2400), тобто: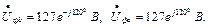
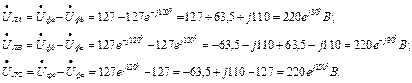


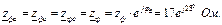
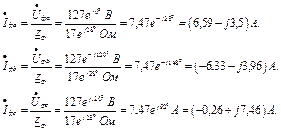
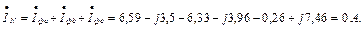
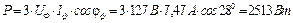 ;
;

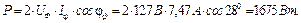
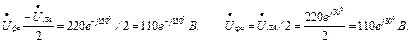
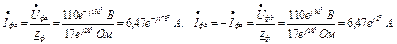





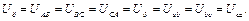
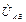 напрямлений вздовж дійсної осі
напрямлений вздовж дійсної осі 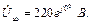
 зсунуті на кути -1200 і 1200 (-2400), тобто:
зсунуті на кути -1200 і 1200 (-2400), тобто: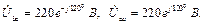

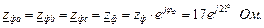
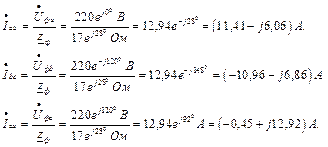
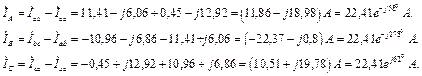
 – активна;
– активна;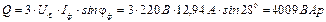 – реактивна;
– реактивна; – повна.
– повна.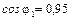 та
та 
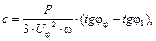
 – колова частота струму.
– колова частота струму.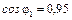
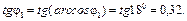
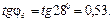
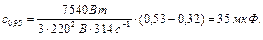

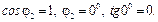

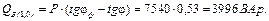
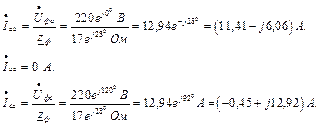
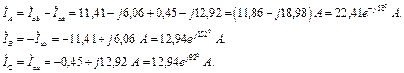
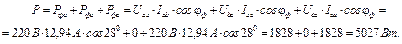



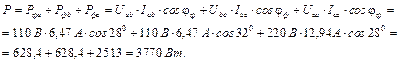



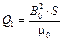 визначаємо магнітну індукцію в повітря-ному проміжку електромагніту:
визначаємо магнітну індукцію в повітря-ному проміжку електромагніту:
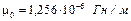 – магнітна стала.
– магнітна стала. , площі поперечного перерізу цих ділянок
, площі поперечного перерізу цих ділянок 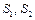 і повітряного проміжку
і повітряного проміжку 
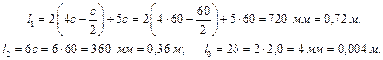


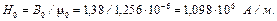
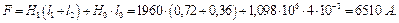
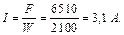
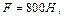 якщо обмотка під’єднана до джерела постійної напруги
якщо обмотка під’єднана до джерела постійної напруги 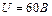 і допустима густина струму
і допустима густина струму  Сердечник і якір електромагніту виготовлені зі сталі, крива намагнічування якої задана в таблиці. Розміри магнітопровода зображені на рис. 23, при цьому а= = 12 см, b = 5см. З метою запобігання прилипання якоря до полюсів електромагніту передбачена прокладка із немагнітного матеріалу, товщиною
Сердечник і якір електромагніту виготовлені зі сталі, крива намагнічування якої задана в таблиці. Розміри магнітопровода зображені на рис. 23, при цьому а= = 12 см, b = 5см. З метою запобігання прилипання якоря до полюсів електромагніту передбачена прокладка із немагнітного матеріалу, товщиною  .
.


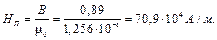

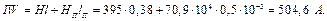
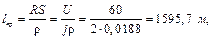

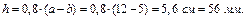
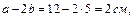 тобто
тобто
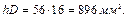

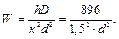
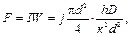
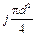 – величина струму в провіднику.
– величина струму в провіднику.
 не перевищує можливої товщини котушки D = 16 мм.
не перевищує можливої товщини котушки D = 16 мм.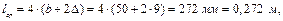


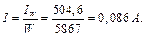
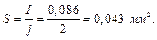
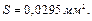
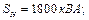

 потужності втрат при неробочому ході
потужності втрат при неробочому ході 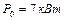 , а при короткому замиканні
, а при короткому замиканні  напруга корот-кого замикання
напруга корот-кого замикання 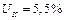 , струм неробочого ходу
, струм неробочого ходу  Визначити: коефіцієнт трансформації; параметри заступної схеми трансформатора; вторинну напругу та струм при під’єднанні споживача з параметрами:
Визначити: коефіцієнт трансформації; параметри заступної схеми трансформатора; вторинну напругу та струм при під’єднанні споживача з параметрами: 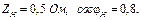

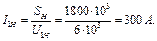
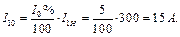
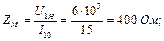
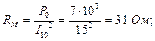

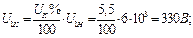

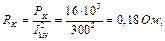
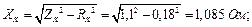


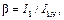 де І 1 – струм первинної обмотки під час навантаження:
де І 1 – струм первинної обмотки під час навантаження: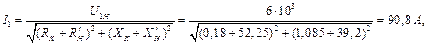
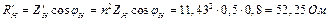 –
– –
–
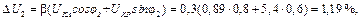
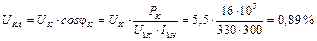 –
–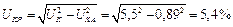 –
–
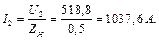
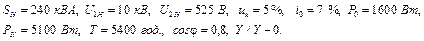




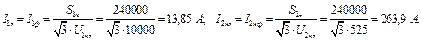
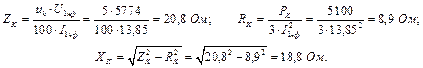
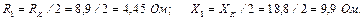
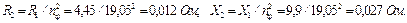
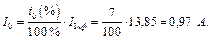
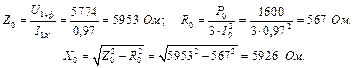
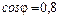 , звідки
, звідки 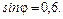
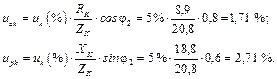
 та
та  знаходимо вторинну напругу та коефіцієнт корисної дії трансформатора.
знаходимо вторинну напругу та коефіцієнт корисної дії трансформатора. , B
, B

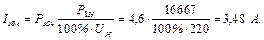





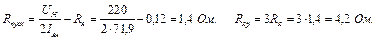

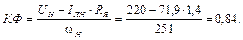


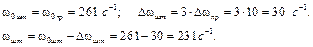



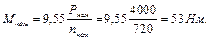
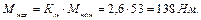

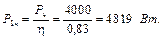
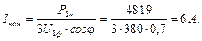


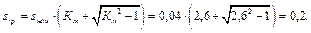

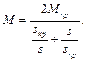

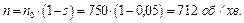
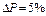 . Коефіцієнти потужностей віток дорівнюють:
. Коефіцієнти потужностей віток дорівнюють: 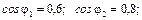
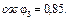 Активні потужності віток:
Активні потужності віток: 
 довжини ділянок:
довжини ділянок: 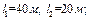
 Номінальна напруга
Номінальна напруга