
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устройств, и построение их лачх и фчхСодержание книги
Поиск на нашем сайте
2.1.1. Основные определения. Операционный усилитель (ОУ) это усилитель постоянного тока с двумя входами (инвертирующим и неинвертирующим), удовлетворяющий (в идеальном варианте) следующим постулатам: 1) коэффициент усиления ОУ стремится к бесконечности 2) входное сопротивление ОУ стремится к бесконечности 3) выходное сопротивление ОУ стремится к нулю 4) если входное напряжение 5) полоса усиливаемых частот стремится к бесконечности ( Очевидно, что на практике эти постулаты полностью не выполняются. Однако в большом числе практических применений они достаточно точно отражают свойства ОУ и значительно упрощают расчёт реальных схем. Так как, согласно последнему постулату ( При описании частотных свойств преобразователя удобно пользоваться понятием его передаточной функции Учитывая второй постулат (
Определим передаточные функции 2.1.2. Вывод передаточной функции Рассмотрим оба варианта. Вариант 1. Допустим, задана цепь ЭЦ-1 (рис. 2.1.1) из таблицы 2.2.
 или или
Перепишем полученное уравнение, разделив члены, содержащие переменные
Переходя к изображениям временных функций f (t)
Откуда передаточная функция рассматриваемого звена
где t = RС - постоянная времени данного звена.
 Вариант 2. Запишем выражение передаточной функция звена, представленного в операторной форме (рис. 2.1.2), воспользовавшись правилом делителя напряжения, Вариант 2. Запишем выражение передаточной функция звена, представленного в операторной форме (рис. 2.1.2), воспользовавшись правилом делителя напряжения,
2.1.3. Вывод передаточной функции
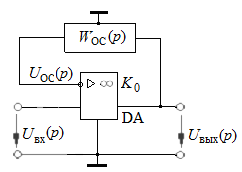 Рассмотрим ОУ (DA) (рис. 2.1.3) с коэффициентом усиления К 0, охваченный цепью последовательной отрицательной обратной связи по напряжению с коэффициентом передачи Рассмотрим ОУ (DA) (рис. 2.1.3) с коэффициентом усиления К 0, охваченный цепью последовательной отрицательной обратной связи по напряжению с коэффициентом передачи
Так как фазы напряжения
приводит к уменьшению выходного напряжения Известно, что ОУ усиливает разность напряжений, приложенных между его неинвертирующим и инвертирующим входами. Поэтому выходное напряжение ОУ в операторной (Лапласа) форме
Откуда передаточная функция ОУ с последовательной ООС по напряжению
П р и м е ч а н и е. В выражении (2.2) учтён пятый постулат ОУ о независимости его коэффициента усиления К 0 от частоты. Если необходимо учесть собственные частотные свойства ОУ, то в полученном выражении значение К 0 необходимо заменить реальной передаточной функцией К ОУ(р) усилителя. 2.1.4. Получение выражения для ЛАЧХ преобразователя сигналов. Передаточную функцию преобразователя
Заменив в (2.3) оператор p оператором j w, где
в которой выделяют действительную
Величина Используя свойства функций lg и arg, выражения (2.4) и (2.5) с учетом выражения (2.3) запишем в следующем виде:
Из выражений (2.6) и (2.7) следует, что интегральные ЛАЧХ и ФЧХ могут быть построены алгебраическим суммированием ЛАЧХ и ФЧХ составляющих многочленов коэффициента передачи В качестве примера построим ЛАЧХ и ФЧХ трех преобразователей (звеньев) аналоговых сигналов с передаточными функциями вида:
Представим передаточную функцию
Найдём выражения ЛАЧХ и ФЧХ этих звеньев с передаточными функциями
Характеристики звена с передаточной функцией
Чтобы избавиться от мнимой единицы в знаменателе, умножим числитель и знаменатель данного выражения на комплексно-сопряженное знаменателю число,
где Модуль передаточной функции
ЛАЧХ и ФЧХ звена:
Характеристики звена с передаточной функцией
Характеристика звена с передаточной функцией
Характеристика звена с передаточной функцией
2.1.5. Расчёт и построение ЛАЧХ и ФЧХ звеньев устройства. Полученные выражения позволяют построить ЛАЧХ и ФЧХ как звеньев, так и устройства в целом. Однако, на практике, вместо реальных ЛАЧХ, строят так называемые диаграммы Боде на двойной логарифмической сетке, являющимися кусочно-линейными аппроксимациями реальных характеристик ЛАЧХ. Для построения диаграмм Боде вычислим значения Передаточная функция При w ® 0 имеем: при w = 1/t2,
при w ® ¥ имеем
 Из выражения функции 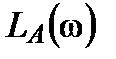 следует, что частота w = 1/t2 является верхней границей полосы пропускания звена (рис. 2.1.4 а). Напомним, что полосой пропускания четырехполюсника называют диапазон частот, в котором его коэффициент передачи уменьшается не ниже 0,707 своего максимального значения, т.е. уменьшается не более, чем на 3 дБ. следует, что частота w = 1/t2 является верхней границей полосы пропускания звена (рис. 2.1.4 а). Напомним, что полосой пропускания четырехполюсника называют диапазон частот, в котором его коэффициент передачи уменьшается не ниже 0,707 своего максимального значения, т.е. уменьшается не более, чем на 3 дБ.
Анализ значений функции Отметим, что на частоте w = 1/t2 коэффициент передачи устройства имеет значение, равное 0,707 K 1, а фазовый сдвиг – значение -p/4, равное половине максимального фазового сдвига -p/2 (см. рис. 2.1.4 б). Передаточная функция при w ® 0 имеем: при w = 1/t1, и при w ® ¥, Анализ значений функции
Передаточная функция  . Найдем значения . Найдем значения  и и  в характерных точках: в характерных точках:
при w ® 0 имеем: при w = 1/t1,
Итак, характеристика  рассматриваемого звена во всем диапазоне частот w имеет постоянный наклон 20дБ/дек при сдвиге фаз между выходным и входным сигналами, равном рассматриваемого звена во всем диапазоне частот w имеет постоянный наклон 20дБ/дек при сдвиге фаз между выходным и входным сигналами, равном  (рис. 2.1.6). При этом характеристика (рис. 2.1.6). При этом характеристика  пересекает ось частоты в точке пересекает ось частоты в точке  (см. рис. 2.1.6 а). (см. рис. 2.1.6 а).
Передаточная функция при w ® 0 имеем: при w = 1/t4,
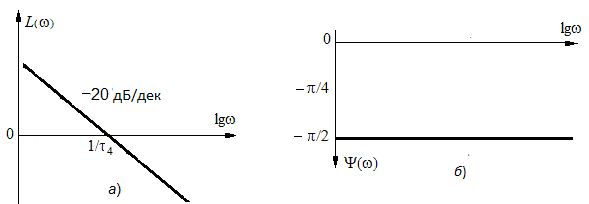 Итак, характеристика  рассматриваемого звена во всем диапазоне частот w имеет постоянный наклон -20дБ/дек при сдвиге фаз между выходным и входным сигналами, равном - рассматриваемого звена во всем диапазоне частот w имеет постоянный наклон -20дБ/дек при сдвиге фаз между выходным и входным сигналами, равном -  (рис. 2.1.7). При этом характеристика (рис. 2.1.7). При этом характеристика  пересекает ось частоты в точке пересекает ось частоты в точке  (см. рис. 2.1.7 а). (см. рис. 2.1.7 а).
Из сопоставительного анализа передаточных функций и характеристик звеньев преобразователя аналоговых сигналов можно сделать несколько практически важных выводов: 1. Если передаточная функция звена содержит множитель t р + 1, то его ЛАЧХ на диаграмме Боде при w > 1/t представляется асимптотой с наклоном +20 дБ/дек, начинающейся на частоте w = 1/t, а ФЧХ на этой частоте имеет фазовый сдвиг между выходной и входной величинами, равный p/4. 2. Если передаточная функция звена содержит множитель 1/(t р + 1), то его ЛАЧХ на диаграмме Боде при w > 1/t представляется асимптотой с наклоном -20 дБ/дек, начинающейся на частоте w = 1/t, а ФЧХ на этой частоте имеет сдвиг фаз между выходным и входным сигналами, равный -p/4. 3. Максимальные сдвиги фаз между выходными и входными сигналами звеньев вида t р + 1 и 1/(t р + 1) равны +p/2 и -p/2. 4. Если числитель передаточной функции звена содержит множитель t р, то во всем диапазоне частот ЛАЧХ звена на диаграмме Боде представляется асимптотой с наклоном +20 дБ/дек (пересекающей ось logw в точке log(1/t)), а сдвиг фаз между выходным и входным сигналами равен +p/2. 5. Если знаменатель передаточной функции звена содержит множитель t р, то его ЛАЧХ на диаграмме Боде во всем диапазоне частот представляется асимптотой с наклоном -20 дБ/дек (пересекающей ось lgw в точке lg(1/t)), а фазовый сдвиг равен -p/2. 6. Если при разложении многочленов передаточной функции W пр(p) преобразователя значения постоянных времени t звеньев с передаточными функциями вида t р и 1/(t р) включены в постоянный коэффициент передачи К пр = W пр(0) преобразователя, то соответствующие асимптоты идеальных дифференцирующего с функцией W (p) = p и интегрирующегос функцией W (p) = 1/ p звеньев диаграммы Боде пересекают ось абсцисс в точке 1 шкалы частот lgw (или в точке 0 шкалы частот w). 7. Результирующие ЛАЧХ и ФЧХ преобразователя могут быть построены суммированием соответствующих характеристик отдельных звеньев. ПРИМЕР ПОСТРОЕНИЯ ЛАЧХ
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.006 с.) |

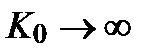 ;
; ;
;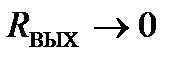 ;
; , то и выходное напряжение
, то и выходное напряжение 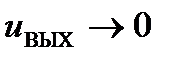 ;
; ).
).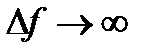 ), ОУ одинаково усиливает сигналы всего спектра входных частот, то требуемые частотные свойства (в частности, коэффициент усиления
), ОУ одинаково усиливает сигналы всего спектра входных частот, то требуемые частотные свойства (в частности, коэффициент усиления  ) реального преобразователя аналоговых сигналов можно получить введением дополнительных частотно зависимых звеньев. Эти звенья (см. рис. 2.1) могут быть включены либо последовательно во входную или выходную цепи ОУ, либо в цепь его обратной связи.
) реального преобразователя аналоговых сигналов можно получить введением дополнительных частотно зависимых звеньев. Эти звенья (см. рис. 2.1) могут быть включены либо последовательно во входную или выходную цепи ОУ, либо в цепь его обратной связи. , фактически отражающей зависимость коэффициента передачи устройства от частоты входного сигнала.
, фактически отражающей зависимость коэффициента передачи устройства от частоты входного сигнала. ), можно полагать, что последовательное звено коррекции (см. рис. 2.1) работает по выходу в режиме холостого хода. В этом случае передаточную функцию всего устройства
), можно полагать, что последовательное звено коррекции (см. рис. 2.1) работает по выходу в режиме холостого хода. В этом случае передаточную функцию всего устройства  можно представить в виде произведения передаточных функций последовательного звена коррекции
можно представить в виде произведения передаточных функций последовательного звена коррекции 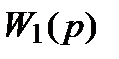 и операционного усилителя
и операционного усилителя  , охваченного частотно зависимой цепью отрицательной обратной связи (ООС) с передаточной функцией
, охваченного частотно зависимой цепью отрицательной обратной связи (ООС) с передаточной функцией  , т.е.
, т.е.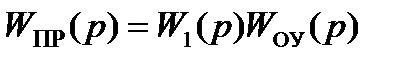 . (2.1)
. (2.1)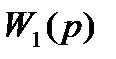 и
и  отдельных звеньев преобразователя.
отдельных звеньев преобразователя. 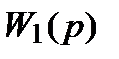 звена коррекции. Передаточную функцию
звена коррекции. Передаточную функцию 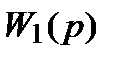 можно получить либо из дифференциального уравнения звена, либо используя его операторную схему замещения.
можно получить либо из дифференциального уравнения звена, либо используя его операторную схему замещения.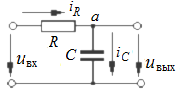
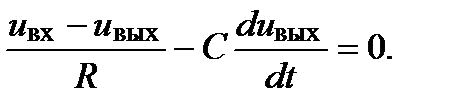
 и
и 
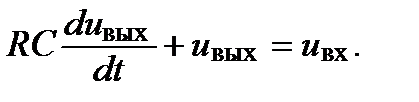
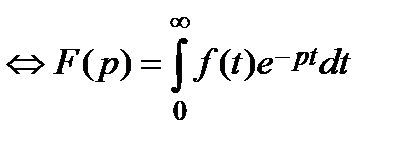 и их производных
и их производных  при нулевых начальных условиях
при нулевых начальных условиях  , получим:
, получим: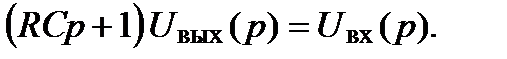
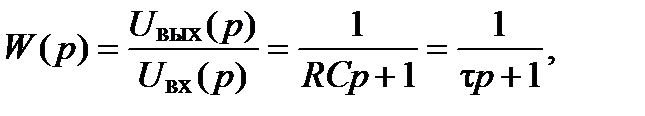
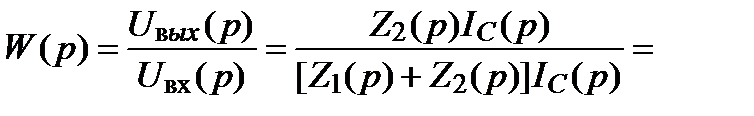

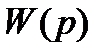 звена идентичны. Очевидно, что вывод функции
звена идентичны. Очевидно, что вывод функции  значительно проще во втором варианте.
значительно проще во втором варианте. усилителя с ООС.
усилителя с ООС. 
 , поступающего на инвертирующий вход ОУ, и выходного напряжения
, поступающего на инвертирующий вход ОУ, и выходного напряжения  сдвинуты относительно друг друга на половину периода, то увеличение напряжения
сдвинуты относительно друг друга на половину периода, то увеличение напряжения


 (2.2)
(2.2) в общем случае можно представить в виде отношения двух многочленов, причем каждый из этих многочленов может быть записан в виде разложения по его собственным корням. Если корни многочленов действительные, то получим выражение:
в общем случае можно представить в виде отношения двух многочленов, причем каждый из этих многочленов может быть записан в виде разложения по его собственным корням. Если корни многочленов действительные, то получим выражение: (2.3)
(2.3) , получают комплексную передаточную функцию преобразователя
, получают комплексную передаточную функцию преобразователя  :
:
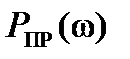 и мнимую
и мнимую 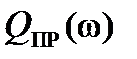 части. Характеристику, построенную в координатах
части. Характеристику, построенную в координатах  и
и 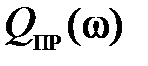 , принято называть амплитудно-фазовой частотной характеристикой (АФЧХ) преобразователя (устройства). Однако, на практике большее распространение получили логарифмическая амплитудно-частотная (ЛАЧХ)
, принято называть амплитудно-фазовой частотной характеристикой (АФЧХ) преобразователя (устройства). Однако, на практике большее распространение получили логарифмическая амплитудно-частотная (ЛАЧХ)  и фазо-частотная (ФЧХ)
и фазо-частотная (ФЧХ) 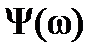 характеристики, полученные в соответствии с выражениями:
характеристики, полученные в соответствии с выражениями: (2.4)
(2.4)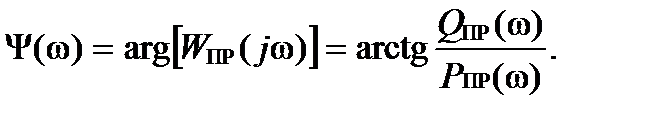 (2.5)
(2.5) измеряется в децибелах [дБ] или в неперах [Нп], а
измеряется в децибелах [дБ] или в неперах [Нп], а  в радианах [рад]. Заметим, что выражение (2.5) справедливо в случае, если
в радианах [рад]. Заметим, что выражение (2.5) справедливо в случае, если 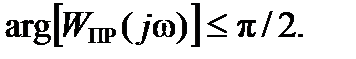
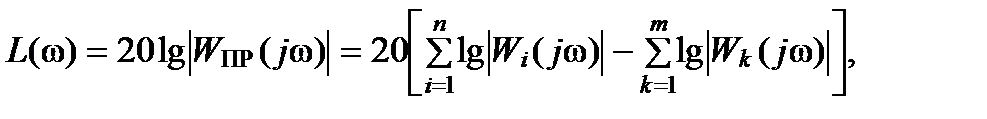 (2.6)
(2.6) (2.7)
(2.7)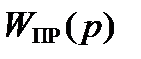 преобразователя (см. (2.3)).
преобразователя (см. (2.3)). ,
,  и
и 
 в виде произведения двух функций
в виде произведения двух функций  и
и 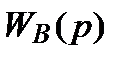 соответственно двух последовательно соединенных звеньев:
соответственно двух последовательно соединенных звеньев: .
.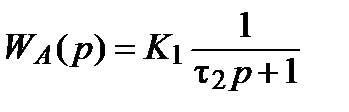 и
и 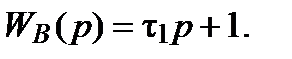
 . Комплексный коэффициент передачи этого звена
. Комплексный коэффициент передачи этого звена
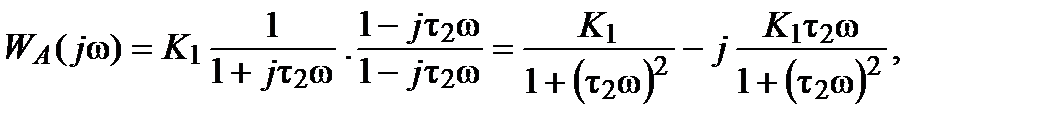
 и
и  .
. равен:
равен: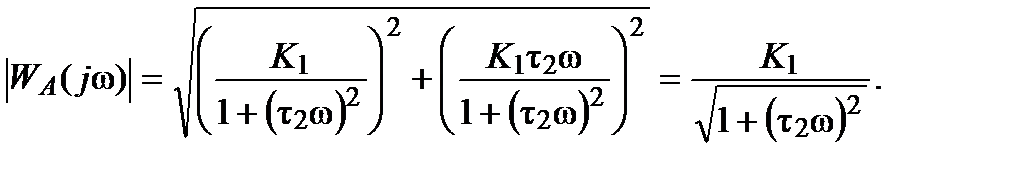
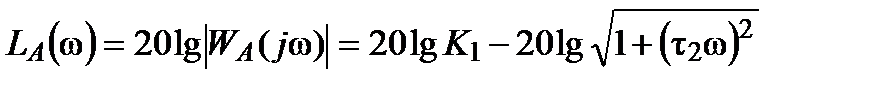 ,
,
 и
и  для второго звена:
для второго звена: ,
,  ,
, 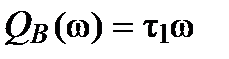 ,
, 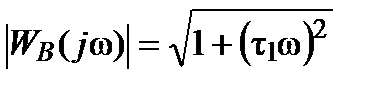 ,
,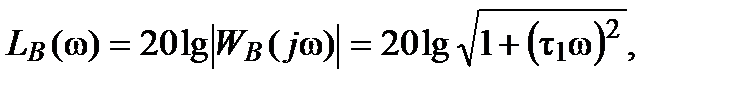

 и
и 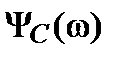 :
: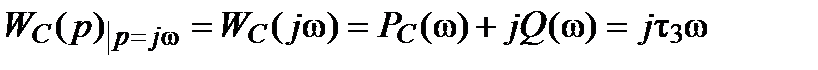 ,
,
 ,
,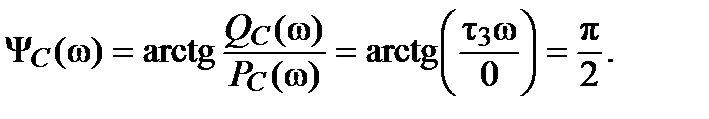
 Запишем выражения функций
Запишем выражения функций  и
и  :
: ,
,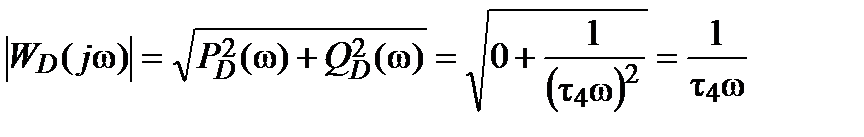 ,
,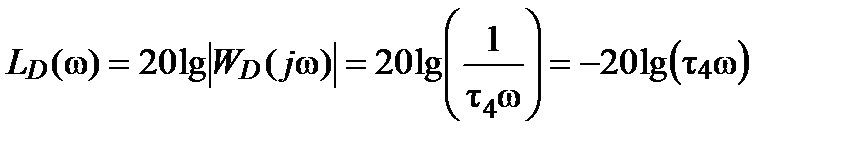 ,
,
 и
и  звеньев в нескольких характерных точках.
звеньев в нескольких характерных точках.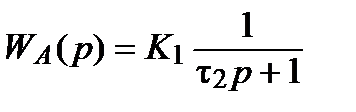 .
.  и
и  ,
, дБ и
дБ и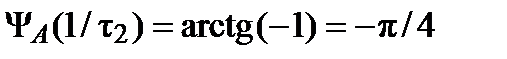 рад,
рад, и
и 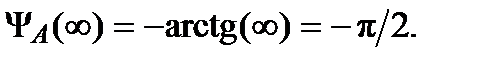
 = K 1/(t2 p + 1)
= K 1/(t2 p + 1)
 показывает, что она линейно падает на 20 дБ при изменении частоты в 10 раз. Поэтому при построении ЛАЧХ удобно использовать логарифмический масштаб частоты.
показывает, что она линейно падает на 20 дБ при изменении частоты в 10 раз. Поэтому при построении ЛАЧХ удобно использовать логарифмический масштаб частоты. . Определим значения
. Определим значения  и
и 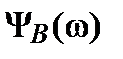 в характерных точках:
в характерных точках: и
и  ,
, дБ
дБ рад,
рад,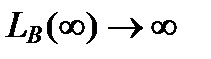 и
и  .
. звена показывает, что реальная характеристика
звена показывает, что реальная характеристика  , как и в предыдущем случае, отличается от асимптотической на 3 дБ (рис. 2.1.5 а). При изменении частоты в 10 раз характеристика звена
, как и в предыдущем случае, отличается от асимптотической на 3 дБ (рис. 2.1.5 а). При изменении частоты в 10 раз характеристика звена 
 = t1 p + 1
= t1 p + 1
 и
и 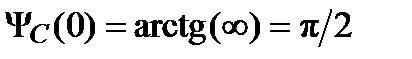 ,
, дБ, при w ® ¥,
дБ, при w ® ¥,  ,
, 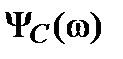 =
=  .
.
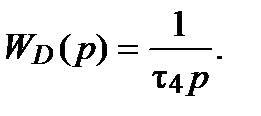 Найдем значения
Найдем значения  в характерных точках:
в характерных точках: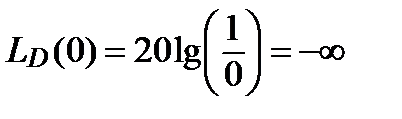 и
и 
 дБ, при w ® ¥,
дБ, при w ® ¥,  ,
, 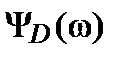 --
--  .
.



