
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывести формулу (1.9) для удельной поверхности фиктивного грунта.Стр 1 из 8Следующая ⇒
А.А. Вольф, М.И. Забоева
ПОДЗЕМНАЯ ГИДРОМЕХАНИКА
Учебное пособие для студентов специальностей: 090600 – Разработка и эксплуатация нефтяных и газовых месторождений, 090800 – Бурение нефтяных и газовых скважин, 090790 – Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ всех форм обучения
Тюмень 2009 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Тюменский государственный нефтегазовый университет» (ТюмГНГУ)
Вольф А.А., Забоева М.И. Учебное пособие. – Тюмень, 2009.?????? с.
Учебное пособие предназначено для студентов, обучающихся по направлению подготовки дипломированных специалистов 650700 – Нефтегазовое дело по специальностям: 090600 – Разработка нефтяных и газовых месторождений, 090800 – Бурение нефтяных и газовых скважин, 090790 – Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ.
© Государственное образовательное учреждение высшего профессионального образования «Тюменский государственный нефтегазовый университет», 2009 Основные понятия и модели пористых сред.
Пористую среду представляют, как множество твердых частиц, плотно прилегающих друг к другу, пространство между которыми может быть заполнено жидкостью или газом. Под пористостью горной породы понимают наличие в ней пустот различной формы и происхождения. Количественно величина пористости определяется коэффициентом пористости m, определяемым для некоторого элемента пористой среды, как отношением объема пор
Различают общую mобщ, открытую mоткр и динамическую (эффективную) mэфф пористость:
где: Коэффициент открытой пористости можно определить методом взвешивания, при котором определяются: масса сухого образца М1, масса образца, на 100 % насыщенного водой М2 и масса образца, на 100% насыщенного водой во взвешенном состоянии в воде М3. Тогда коэффициент открытой пористости равен:
Другой способ (газоволюметрический) определения открытой пористости основан на применении закона Бойля-Мариотта. Идеальный газ из калибровочного сосуда с известным объемом V0 при известном давлении p0 перетекает в поровое пространство сухого образца объемом Vобр, находящимся в непроницаемой манжете и обжатого со всех сторон «горным» давлением. При этом давление внутри замкнутой системы сосуд – образец устанавливается до значения р. Тогда объем пор
где V* - «мертвый» объем трубок соединяющих калибровочный сосуд с образцом, а коэффициент открытой пористости определяется из соотношения (1.2). Отметим, что в процессе всего эксперимента поддерживается постоянная температура. Коэффициентом просветности n называется отношение площади просветов Sпросв в данном сечении пористой среды ко всей площади этого сечения S:
Среднее по длине пласта значение просветности равно пористости. Модель фиктивного грунта состоит из шариков одного диаметра уложенных определенным образом, рис. 1. Основным элементом фиктивного грунта является ромбоэдр, который получается, если принять центры восьми соприкасающихся частиц за вершины углов. Пористость m и просветность n ячейки Шлихтера изменяются по закону:
Удельная поверхность – это суммарная площадь поверхности частиц, которые содержатся в единице объема пористой среды:
Для фиктивного грунта:
Эффективный диаметр частиц фиктивного грунта Измельченный грунт просеивают через набор сит с различной площадью отверстий, разделяя и взвешивая фракции. Затем строят кривую механического состава, откладывая по оси абсцисс средние диаметры di фракций, а по оси ординат – сумму масс фракций в процентах от общей массы
За средний диаметр каждой фракции принимают среднее арифметическое крайних диаметров d’:
Эффективный диаметр определяют по гранулометрическому составу, н.п. по формуле веса средней частицы
где di - средний диаметр i -ой фракции; ni - массовая или счетная доля i -ой фракции. Эмпирические способы определения По Газену:
По методу Крюгера - Цункера:
Капиллярная модель пористой среды (идеальный грунт) – система прямых трубок малого диаметра одинакового сечения длиной Для капиллярной модели имеется связь радиуса трубок (пор) с диаметром частиц фиктивного грунта:
Скоростью фильтрации v называется отношение объемного расхода жидкости Q к площади поперечного сечения F, нормального к направлению движения жидкости.
Скорость фильтрации v и истинная (средняя) скорость движения жидкости
Задачи к разделу 1
Задача 1.1 Вывести формулу Шлихтера для свободной упаковки частиц (q =900) и для более плотной (q =600). Задача 1.2 Определить коэффициенты пористости и просветности ячейки Шлихтера, если угол укладки частиц a равен 600, 700, 800, 900. Построить график зависимости данных величин от угла укладки. Задача 1.3 Определите удельную поверхность песка, пористость которого равна
Задача 1.4 Задача 1.5 Построить кривую механического анализа и определить эффективный диаметр песчинок по способам Газена и Крюгера-Цункера по следующим гранулометрическим составам:
Задача 1.6 Оценить удельную поверхность образца и число частиц N в образце для свободной упаковки частиц (q = 900), если до измельчения его диаметр d = 2,54 см, а длина L = 3 см. Средний диаметр зерен взять из решений задачи 1.4 методом Крюгера Цункера.
Задача 1.7 Сопоставить число частиц диаметром d, заключенных в 1 м3 фиктивного грунта (N / V), при наиболее свободном расположении частиц (q = 900) и при наиболее плотном их расположении(q = 600).
Задача 1.8 Определить удельную поверхность Sуд фиктивного грунта и радиус пор идеального грунта r, если эффективный диаметр частиц dэф =0,11мм, а угол упаковки q = 750.
Задача 1.9 Определить скорость фильтрации и среднюю скорость движения воды при установившемся потоке через цилиндрический образец диаметром d = 2,54 см, если известно, что расход через образец Q =0,7см3/мин, масса сухого образца М1 = 116,3 г, масса образца, на 100% насыщенного водой М2 = 126,49 г, а масса образца, на 100% насыщенного водой во взвешенном состоянии в воде М3 = 72,03 г. Сжимаемостью образца пренебречь.
Задача 1.10 Определить скорость фильтрации и среднюю скорость движения нефти у стенки гидродинамически совершенной скважины и на расстоянии r = 75 м, если известно, что мощность пласта h = 10 м, коэффициент пористости m = 18%, радиус скважины rс = 0,1 м, массовый дебит скважины Qm = 50 т/сут и плотность нефти r =0,85г/см3. Жидкость считать несжимаемой.
Задачи к разделу 2
Задача 2.1 Из аналогии законов Дарси и Пуазейля найти пористость, проницаемость и удельную поверхность капиллярной модели с плотностью капиллярных каналов n/ (число каналов на единицу площади поперечного сечения) и радиусом r.
Задача 2.2 Определить коэффициент фильтрации, если известно, что площадь поперечного сечения горизонтально расположенного образца песчаника S = 30 см2, длина образца L = 15 см, разность давлений на входе жидкости в образец и на выходе Dp = 19,6 кПа, плотность жидкости ρ = 1000 кг/м3 и расход Q = 5 л/час.
Задача 2.3 Определить коэффициент пористости, если известно, что скорость движения жидкости через образец, определяемый с помощью индикатора, равна vср = 3×10-2 см/сек, коэффициент проницаемости k =0,2 Д, динамическая вязкость m = 4 мПа×с, а разность давления Dp =2кгс/см2 при длине образца L =15 см.
Задача 2.4 Определить коэффициенты проницаемости и фильтрации для цилиндрического образца пористой среды диаметром d = 5 см, длиной L = 20 см, если разность давлений на концах образца составляет 300 мм рт.ст., расход жидкости Q = 0,017 л/ч, динамический коэффициент вязкости жидкости μ = 5 мПа·с, плотность её ρ = 0,85 г/см3. Найти также скорость фильтрации и среднюю скорость движения, если известно, что объем пор составляет Vп =74.6 см3.
Задача 2.5 Через два однородных одинаковых образца пористой среды, содержащих глинистые частицы, пропускали: а) пресную воду при t = 20°C при перепаде давления Dр = 500 мм рт. ст. с расходом Q = 2 см3/мин; б) соленую воду с удельным весом g = 11030 кг/м2с2 и вязкостью m=1,1 сПз при той же разности давления, что и в случае а) и с расходом Q = 0,12 см3/с. Размер образцов: длина L = 5 см, площадь поперечного сечения F =5см2. Определить коэффициент проницаемости и коэффициент фильтрации в обоих случаях. Найти отношение проницаемостей для случаев а) и б). Объяснить полученный результат.
Задача 2.6 Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q =200 м3/сут проницаемость пласта k = 0,2Д, мощность пласта h = 5м, пористость пласта m =16%, динамический коэффициент вязкости m =5сПз, плотность нефти r =0,8 г/см3, радиус гидродинамически совершенной скважины rс =0,1 м.
Задача 2.7 Определить критический дебит скважины в т/сут (дебит, при превышении которого в призабойной зоне нарушается закон Дарси), если известно, что проницаемость пласта k = 1Д, мощность пласта h =20м, пористость пласта m =18%, динамический коэффициент вязкости m =5 сПз, плотность нефти r = 0,85 г/см3, радиус скважины rс. Указание: При определении значения числа Рейнольдса пользоваться формулой Щелкачёва, при Reкр=1
Задача 2.8 Определить скорость фильтрации жидкости через пористую среду при Reкр = 0,1 (по Миллионщикову). Абсолютная проницаемость среды k =1Д, динамический коэффициент вязкости m = 1 мПа·с, плотность жидкости r = 1000 кг/м3, пористость среды m = 0,2.
Задача 2.9 Определить радиус призабойной зоны rкр, в которой нарушен закон Дарси, при установившейся плоскорадиальной фильтрации нефти, если известно, что массовый дебит скважины Qm = 210 т/сут, мощность пласта h = 40 м, проницаемость k = 0,6 Д,пористость пласта m = 19%, динамический коэффициент вязкости нефти в пластовых условиях m =18.10-3 Па. с, а ее плотность ρ = 0,75 г/см3. Указание. В решении использовать число Рейнольдса рассчитанное по формуле М. Д. Миллионщикова при Reкр = 0,022. Задачи к разделу 3
Задача 3.1 Вывести формулу средневзвешенного по объему порового пространства давления
для различных видов течения несжимаемой жидкости и вычислить его при следующих исходных данных: рк =30 МПа, рс(рг)= 10 МПа, Rк(L)= 1 км, rс =0,1 м. Указание. Интегрирование вести: 1) для плоскопараллельного течения от 0 до L. 2) для плоскорадиального от rс до Rk, пренебречь членами, содержащими rс2, как малые по сравнению с Rk2. 3) для радиально-сферического от rс до Rk, пренебречь членами, содержащими rс3 и rс2.
Задача 3.2 Определить дебит дренажной галереи шириной B = 100 м, если мощность пласта h = 10м, расстояние до контура питания L = 10км, коэффициент проницаемости к = 1 Д, коэффициент динамической вязкости m = 1сПз, давление на контуре питания рк = 9,8 МПа и в галерее рг = 7,35 МПа.
Задача 3.3 Показать графически распределение давления и найти градиент давления при плоскопараллельном движении несжимаемой жидкости в пласте, длина которого L = 5км, мощность пласта h = 10м, ширина галереи B = 300м, коэффициент проницаемости k = 0,8Д, коэффициент динамической вязкости m = 4сПз, давление на галерее рг = 2,94 МПа, дебит галереи Q = 30м3/сут.
Задача 3.4 Определить величину коэффициента проницаемости (в различных системах единиц) для случая плоскопараллельного установившегося движения однородной жидкости в пласте по закону Дарси по следующим исходным данным: гидравлический уклон
Задача 3.5 Определить массовый дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания рк = 9,8 МПа, давление на забое скважины рс = 7,35 МПа, проницаемость пласта k =500мД, мощность пласта h = 15м, диаметр скважины Dc = 24,8 см, радиус контура питания Rk =10 км, динамический коэффициент вязкости жидкости m = 6сПз и плотность жидкости r = 850кг/м3.
Задача 3.6 Определить давление на расстоянии 10 и 100 м от скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая что, мощность пласта h = 10м, коэффициент проницаемости k = 0,5 Д, коэффициент динамической вязкости нефти m = 4сПз, плотность нефти r = 870кг/м3, давление на забое скважины рс = 7,84 МПа, массовый дебит скважины Qm = 200т/сут, радиус скважины rc = 12,4см.
Задача 3.7 Определить коэффициент продуктивности и построить индикаторную линию при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, если известно что, давление на контуре питания рк = 8,82МПа, радиус контура питания Rк = 10км, мощность пласта h = 10м, коэффициент проницаемости k =600мД, коэффициент динамической вязкости нефти m = 5сПз, диаметр скважины Dc = 24,8 см.
Задача 3.8 Определить значение коэффициента гидропроводности пласта в Д×см/сПз, если известно, что фильтрация происходит по закону Дарси, коэффициент продуктивности К = 18т/(сут (кгс/см2)), радиус контура питания Rk = 1400 м, плотность нефти r = 925 кг/м3, радиус скважины rc =0,1 м.
Задача 3.9 Определить время отбора нефти из призабойной зоны скважины радиусом r0 = 100м, а также время, за которое частица жидкости пройдет расстояние от контура питания Rk =1,5км до стенки скважины rc =0,1 м, если мощность пласта h = 10м, коэффициент пористости m = 20%, массовый дебит скважины Qm = 40т/сут, плотность нефти r = 920 кг/м3.
Задача 3.10 Как изменится: а) дебит скважины при D р = const, и б) разность давлений между контуром питания и стенкой скважины при Q = const, если увеличить радиус скважины вдвое? 1. Движение происходит по линейному закону фильтрации. 2. Фильтрация происходит по закону Краснопольского. Начальный радиус скважины rc =0,1 м. Расстояние до контура питания Rk = 5 км. Задача 3.11 Во сколько раз необходимо увеличить радиус скважины, чтобы дебит ее при прочих равных условиях удвоился? 1) Движение жидкости происходит по закону Дарси. 2) Жидкость фильтруется по закону Краснопольского. Начальный радиус скважины rc =0,1 м. Расстояние до контура питания Rk = 1 км Задача 3.12 В центре кругового пласта расположена действующая скважина. Определить пьезометрическую высоту H в простаивающей скважине которая находится на расстоянии r = 200 м, если известно, что дебит действующей скважины Q = 30м3/сут, мощность пласта h = 20м, коэффициент проницаемости k = 700 мД, коэффициент динамической вязкости нефти m = 4сПз, радиус контура питания Rk = 5км, давление на контуре питания рк = 12,75МПа. Задача 3.13 Определить относительное понижение пьезометрического уровня d:
в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях 1 м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси. Радиус скважины rc = 10 см, расстояние до контура питания Rк =100 км.
Задача 3.14 Сколько жидкости следует закачивать в пласт в единицу времени через нагнетательную скважину, если необходимо, чтобы давление на стенке скважины поддерживалось в процессе закачки на D р = 1,47МПа выше давления, установившегося в пласте на расстоянии r = 2 км от скважины? Имеет место закон Дарси. мощность пласта h = 10м, коэффициент проницаемости k = 150 мД, коэффициент динамической вязкости нефти m = 1сПз, радиус скважины rс = 10 см.
Функция Лейбензона.
При установившейся изотермической фильтрации сжимаемой жидкости и газа закон Дарси и вытекающие из него формулы, выведенные в предыдущем параграфе, не выполняются, так как объемный расход Q в этих законах в условиях сжимаемости возрастает по мере падения давления за счет расширения жидкости или газа. Одинаковым остается массовый расход Qm ,, что вытекает из условия сплошности и неразрывности потока:
Л.С. Лейбензон впервые ввел потенциальную функцию:
Тогда закон Дарси можно переписать, введя понятие массовой скорости фильтрации
где Проведя такую аналогию можно сделать вывод, что все формулы полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси можно использовать и для установившейся фильтрации сжимаемой жидкости и газа при тех же граничных условиях со следующей заменой переменных:
Например, формула Дюпюи в условиях сжимаемости будет иметь вид:
Остается определить вид функции Лейбензона для различных сжимаемых флюидов. 1. Для сжимаемой жидкости выполняется следующее уравнение состояния, полученное из закона Гука:
где bж – коэффициент сжимаемости жидкости. При
Тогда точное значение функции Лейбензона для сжимаемой жидкости равно:
а приближенное:
т.е. можно считать жидкость несжимаемой. 2. Для идеального газа уравнение состояния Менделеева - Клайперона при изотермическом течении можно записать так:
где rат - плотность газа при атмосферном давлении и пластовой температуре. Функция Лейбензона для идеального газа имеет вид:
А) Для плоско-параллельной фильтрации идеального газа массовый дебит на галерее скважин:
Приведенным расходом Qат назовем объемный расход, приведенный к атмосферному давлению и пластовой температуре:
Тогда из 4.11 получим:
Используя (3.3) получим распределение давления при фильтрации идеального газа, рис.5:
В) При плоскорадиальной фильтрации формула для приведенного дебита газовой скважины (аналог формулы Дюпюи (3.5)) будет иметь вид:
Индикаторную линию для газов строят в координатах Используя (3.7) получим распределение давления в круговом пласте для идеального газа:
В случае плоскорадиальной фильтрации идеального газа по двучленному закону фильтрации приведенный дебит скважины можно определить из формулы:
При этом индикаторные линии газовых скважин, в призабойной зоне которых заведомо нарушается закон Дарси, строят в координатах
где:
Задачи к разделу 4
Задача 4.1 Вывести зависимость дебита идеального газа совершенной скважины от депрессии на круговой пласт с радиусом Rк, если радиус скважины rс, вязкость μ, давление на контуре и забое pк, pс, мощность пласта h, а фильтрация происходит по закону Форшгеймера.
Задача 4.2 В пласте имеется установившаяся плоскорадиальная фильтрация идеального газа по закону Дарси. Давление на контуре питания pк = 9,8 МПа, на забое pс = 6,86 МПа, приведённый к атмосферному давлению объёмный расход газа Qат = 8∙105 м3/сут. Радиус контура питания Rк =750 м, скважины rс = 0,1 м, мощность пласта h = 10 м, пористость m = 20%. Определить давление, скорость фильтрации и истинную среднюю скорость движения газа на расстоянии r =50 м от скважины.
Задача 4.3 Определить скорость фильтрации и среднюю скорость движения при плоскорадиальной фильтрации идеального газа к совершенной скважине у ее стенки rс = 0,1м и на расстоянии r =150 м от центра скважины, если давление в этой точке равно р = 7,84МПа, мощность пласта h =12 м, его пористость m = 20%, а приведенный к атмосферному давлению и пластовой температуре дебит Qат =2×106 м3/сут.
Задача 4.4 Определить радиус призабойной зоны rкр, в которой нарушается закон Дарси, при плоскорадиальной фильтрации идеального газа, если известно, что приведенный к атмосферному давлению при пластовой температуре Qат =2·106 м3/сут, мощность пласта h = 10 м, коэффициент пористости пласта m = 19 %, коэффициент проницаемости k = 0,6 Д, динамический коэффициент вязкости газа в пластовых условиях μ =1,4×10-5кг/м×с, плотность газа при атмосферном давлении и пластовой температуре rат =0,7кг/м3. Указание: Использовать формулу Миллионщикова и взять Reкр =0,022
Задача 4.5 Дебит газовой скважины, приведенный к атмосферному давлению при пластовой температуре Qат =2·106 м3/сут, абсолютное давление на забое рс =7,84 МПа, мощность пласта h = 10 м, коэффициент пористости пласта m = 18 %, коэффициент проницаемости k = 1,2 Д, средняя молекулярная масса газа 18 г/моль, динамический коэффициент вязкости газа в пластовых условиях μ = 0,015 мПа·с, температура пласта T= 45°С. Определить, имеет ли место фильтрация по закону Дарси в призабойной зоне совершенной скважины радиусом rс = 0,1 м (по Щелкачёву и Миллионщикову). Задача 4.6 Совершенная скважина расположена в центре кругового пласта радиуса Rк = 10 км, мощность пласта h = 15 м, коэффициент проницаемости k = 400 мД, вязкость жидкости μ = 1,02 мПа∙с, коэффициент сжимаемости βж = 4,64∙10-10 Па-1. Давление на контуре pк = 11,76 МПа, забойное рс =7,35 МПа, радиус скважины rс = 0,1 м. Фильтрация подчиняется закону Дарси. Определить различие в объёмном суточном дебите скважины, подсчитанным с учётом и без учёта сжимаемости жидкости. Сделать вывод по полученным результатам. Указание: Зависимость плотности жидкости от пластового давления считать по формуле (4.5). Задача 4.7 Определить расстояние r от возмущающей газовой скважины до точки пласта, в которой давление равно среднеарифметическому от забойного pс =70атм и контурного pк =100 атм. Радиус контура питания Rк = 1000 м, радиус скважины rс = 10 см. Задача 4.8 Определить объёмный, приведённый к атмосферному давлению и массовый дебиты совершенной скважины, считая, что фильтрация происходит по закону Дарси, если мощность пласта h = 25 м, проницаемость k = 250 мД, вязкость газа m = 0,014 мПа∙с, плотность газа при нормальных условиях rат = 0,650 кг/м3, радиус скважины rс = 0,1 м, расстояние до контура питания Rк = 900 м, абсолютное давление на забое скважины pс = 2,94 МПа и на контуре питания pк = 3,92 МПа. Газ считать идеальным.
Задача 4.9 Найти коэффициенты А и В уравнения (4.18) индикаторной кривой, а также коэффициент гидропроводности по данным испытания газовой скважины радиусом rс = 0,1 м, работающей в круговом пласте радиусом Rк = 1000 м.
Задача 4.10 Построить распределение давления при стационарной фильтрации упругой жидкости (плотность при атмосферном давлении и пластовой температуре r =850кг/м3) между двумя рядами скважин с давлением рк =51атм в нагнетательном ряду и массовым расходом Qm = 50т/сут на добывающем ряду. Расстояние между рядами L = 5000м. Значения параметров пласта и жидкости следующие: k =1Д, h =10 м, bж =10-101/Па, В =1000м. Определить давление на забоях скважин в добывающем ряду. Сравнить результаты с фильтрацией несжимаемой жидкости при тех же условиях и сделать вывод. Указание: Зависимость плотности жидкости от пластового давления считать по формуле (4.5).
Задачи к разделу 5
Задача 5.1 Определить скорость фильтрации у входа в скважину несовершенную по степени вскрытия, если мощность пласта h =25 м, относительное вскрытие пласта
Задача 5.2 Гидродинамически несовершенная скважина, вскрывает пласт мощностью 20 м на глубину 10 м. Радиус скважины 10 см, а радиус контура питания – 200м. Каково превышение фактического дебита, определенного по формуле Маскета, над дебитом в случае строго плоскорадиального потока к скважине с частичным вскрытием пласта?
Задача 5.3 Используя графики Щурова, найти коэффициенты, определяющие дополнительные фильтрационные сопротивления, обусловленные несовершенством по степени и по характеру вскрытия, а также приведенный радиус и коэффициент совершенства скважины, считая, что диаметр скважины равен 24 см. Скважина вскрывает пласт с радиусом контуром питания 500 м, мощностью 9,6 м на величину 5,76 м. Число прострелов на 1 м вскрытой мощности пласта равна 13 отв/м, глубина проникновения пуль в породу 12 см, диаметр отверстий 0,48 см.
Задача 5.4 Скважину исследовали по методу установившихся отборов, изменяя диаметр штуцера и замеряя забойное давление глубинным манометром. Результаты приведены в таблице:
Определить коэффициент проницаемости, если мощность пласта h =32 м, вскрытие пласта b =21,4м, диаметр скважины Dc =20 см, число прострелов на 1 м вскрытой мощности пласта равна n =10 отв/м, глубина проникновения пуль в породу l’ =10 см, диаметр отверстий d0 =1,2см, радиус контура питания Rk = 300м, динамический коэффициент скважины m = 4сПз.
Задача 5.5 Какому коэффициенту С = С1 + С2, определяющему дополнительное фильтрационное сопротивление обусловленное несовершенством скважины, соответствует коэффициент совершенства d = 0,75? Радиус скважины rc = 0,1 м, радиус контура питания Rk = 1км. Определить также приведенный радиус скважины.
Задача 5.6 Определить значение числа Рейнольдса по формулам Щелкачева и Миллионщикова у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована. На каждом погонном метре колонны прострелено 10 отверстий диаметром d0 =10мм, мощность пласта h = 15м, проницаемость пласта k = 1Д, пористость т = 18%, коэффициент вязкости нефти m = 4 сПз, плотность нефти ρ = 870 кг/м3 и дебит скважины составляет 140м3/сут.
Задачи к разделу 3
Задача 6.1 Совершенная скважина радиуса rс = 0,1 м работает в пласте, ограниченном двумя непроницаемыми границами, расположенными под углом 900. Расстояния до границ равны a = 150 м, b = 300 м, расстояние до контура питания Rк = 8 км, давление на границах (контурах питания) pк = 11,76 МПа, давление на забое pс = 9,8 МПа. Мощность пласта h = 12м, вязкость жидкости μ = 3 мПа∙с, проницаемость пласта k = 700мД. Найти дебит скважины.
Задача 6.2 В полубесконечном пласте мощностью h = 10 м с прямолинейным контуром питания работает совершенная добывающая скважина, расположенная на расстоянии a = 300 м от контура, с дебитом 50 т/сут. Определить скорость фильтрации: а) у стенки скважины; б) в точке А, расположенной на контуре питания и отстоящей на
в) в точке В, расположенной (под углом от скважины) на расстоянии c = 150 м от скважины вдоль перпендикуляра, опущенного из скважины на контур питания и d = 200 м от этого перпендикуляра вдоль контура (см. рис.21).
Задача 6.3 Определить дебит батареи из четырех скважин, расположенных вдали от контура питания, и одной скважины, находящейся в центре (см. рисунок 22), если известно, что все скважины находятся на окружности радиуса R1 = 200м (радиус батареи) на одинаковом расстоянии друг от друга и работают в одинаковых условиях. Расстояние до контура питания Rк = 10км, радиус скважин rс = 0,1м, мощность пласта h = 10м, потенциал на контуре Фк = 40см2/сек, а на скважинах Фс = 30см2/сек. Задача 6.4 Круговой нефтяной пласт радиусом Rк = 15км, мощностью h = 8м, эксплуатируется пятью скважинами радиусом rc = 7,5 см, из которых четыре расположены в вершинах квадрата со стороной d = 150 м, а пятая в центре (рис. 22). Давление на контуре рк = 11МПа, забойные давления на всех скважинах одинаковы и равны рс = 90атм. Коэффициент проницаемости k = 0,6 Д, вязкость нефти m = 1,1 сПз. Определить дебиты скважин и отношения дебитов Q5/Q1.
Задач
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 2825; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.77 (0.19 с.) |
 в этом элементе к его общему объему
в этом элементе к его общему объему  (измеряется в долях или процентах):
(измеряется в долях или процентах): (1.1)
(1.1) ;
;  ;
; 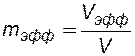 (1.2)
(1.2) - объем всех пор;
- объем всех пор;  - объем сообщающихся пор;
- объем сообщающихся пор;  - часть объема открытых пор, через которые может фильтроваться жидкость.
- часть объема открытых пор, через которые может фильтроваться жидкость.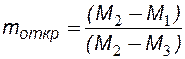 (1.3)
(1.3) (1.4)
(1.4)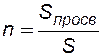 (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7)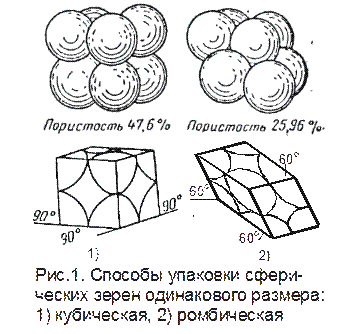 где q - угол, определяющий способ упаковки шариков одинакового размера (600 < q < 900)
где q - угол, определяющий способ упаковки шариков одинакового размера (600 < q < 900) (1.8)
(1.8) (1.9)
(1.9) , при котором его гидравлическое сопротивление совпадает с гидравлическим сопротивлением реального грунта определяется в результате гранулометрического (механического) анализа.
, при котором его гидравлическое сопротивление совпадает с гидравлическим сопротивлением реального грунта определяется в результате гранулометрического (механического) анализа. , рис.2.
, рис.2.

 (1.10)
(1.10)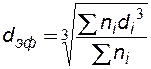 (1.11)
(1.11)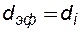 при
при  (1.12)
(1.12) (1.13)
(1.13) .
. (1.14)
(1.14) (1.15)
(1.15)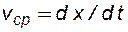 связаны соотношением:
связаны соотношением: (1.16)
(1.16)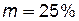 и эффективный диаметр
и эффективный диаметр  мм, а также найти число частиц в единице объема среды N / V.
мм, а также найти число частиц в единице объема среды N / V. ,мм
,мм
 %
%
 :
: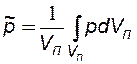 ,
, = 0,03, ширина галереи В = 500 м, мощность пласта h = 6 м, плотность жидкости r =850кг/м3, абсолютная вязкость m = 5сПз и дебит галереи Q = 30м3/сут.
= 0,03, ширина галереи В = 500 м, мощность пласта h = 6 м, плотность жидкости r =850кг/м3, абсолютная вязкость m = 5сПз и дебит галереи Q = 30м3/сут.
 (4.1)
(4.1) (4.2)
(4.2) :
: или
или  , (4.3)
, (4.3) .
.
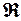
 (4.4)
(4.4) (4.5)
(4.5) (например, для воды bж » 4,5×10-101/Па) экспоненту можно разложить в ряд и ограничиться первыми двумя членами разложения можно приближенно записать:
(например, для воды bж » 4,5×10-101/Па) экспоненту можно разложить в ряд и ограничиться первыми двумя членами разложения можно приближенно записать: (4.6)
(4.6) , (4.7)
, (4.7)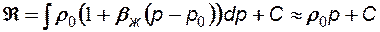 (4.8)
(4.8) Þ
Þ 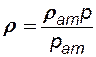 (4.9)
(4.9) (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14) (4.15)
(4.15) и
и 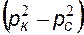 .
. (4.16)
(4.16) (4.17)
(4.17) , и тогда формула для обработки таких линий принимает следующий вид:
, и тогда формула для обработки таких линий принимает следующий вид: (4.18)
(4.18)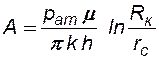 ,
,  .
. =0,6, радиус скважины rс = 0,1м, дебит скважины Q = 250м3/сут.
=0,6, радиус скважины rс = 0,1м, дебит скважины Q = 250м3/сут. b = 500м от места пересечения линии контура питания с перпендикуляром, опущенным из скважины на контур питания (см. рис.21);
b = 500м от места пересечения линии контура питания с перпендикуляром, опущенным из скважины на контур питания (см. рис.21);


