
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухфазная фильтрация несмешивающихся жидкостей, вытеснение нефти водой. Функция бакли – леверетта. ⇐ ПредыдущаяСтр 8 из 8
Углеводородные системы могут быть гомо- и гетерогенными. В гомогенной системе все ее части имеют одинаковые физические и химические свойства. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза - это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами. Насыщенностью i -й фазы si называется доля объема порового пространства, занятого этой фазой:
Сумма всех насыщенностей в поровом объеме равна единице. Если поровое пространство пористой среды заполнено только двумя жидкостями - нефтью и водой, то тогда выполняется соотношение:
где sн, sв - соответственно насыщенности нефтью и водой. Далее введем обозначения:
В общем случае при описании двухфазной фильтрации увеличивается число параметров, подлежащих определению, что существенно усложняет теоретическое исследование. Далее, рассмотрим наиболее простое, с точки зрения математического моделирования, одномерное двухфазное течение, соответствующее вытеснению жидкости, первоначально заполнявшей поры, другой жидкостью, не смешивающейся с первой, впервые предложенное американскими исследователями С. Бакли и М. Левереттом (1942 г.). Нефть вытесняется водой в прямолинейном тонком горизонтальном образце, который представлен однородной изотропной пористой средой при следующих допущениях: 1) вода, нефть и пористая среда несжимаемы, т. е.:
2) капиллярные силы пренебрежимо малы, т.е. пластовое давление в нефти и воде одинаковое:
3) влияние массовых сил не учитывается; 4) температура постоянна; 5) фазовые переходы и химические реакции отсутствуют. С учетом сделанных допущений и (8.3), уравнения неразрывности для воды и нефти примут вид:
Сложив уравнения (8.4) и (8.5) получим:
Уравнение (8.6) показывает, что суммарная скорость двухфазного потока v(t) (или суммарный расход обеих жидкостей Q(t)) не зависит от координаты x и является либо постоянной величиной, либо известной функцией времени:
Скорости фильтрации воды
где
Отметим, что произведение k на Относительные фазовые проницаемости Типичные экспериментальные кривые фазовых проницаемостей, определяемые при совместной фильтрации воды и нефти, приведены на рисунке 28.
Отметим некоторые характерные особенности этих кривых. Для каждой жидкости существует предельная насыщенность, такая, что при меньших значениях насыщенности эта жидкость неподвижна. Движение воды может происходить только в том случае, если
Относительная проницаемость смачивающей фазы (воды)
Разделив уравнение (8.8) на сумму уравнений (8.8) и (8.9), с учетом (8.7), можно получить:
где Функция F(s) имеет простой физический смысл – объемная доля воды в суммарном потоке двух несмешивающихся жидкостей. Функция Бакли – Леверетта играет важную роль при гидродинамических расчетах двухфазных потоков, определяя полноту вытеснения и характер распределения насыщенности по пласту. Характерный вид функции Бакли-Леверетта представлен на рис. 29. Из (8.11) следует:
Подставив (8.12) в (8.8) и используя правило дифференцирования сложной функции, получим уравнение только относительно s:
где Уравнение (8.13) решается методом характеристик:
где x0 координата с начальной водонасыщенностью s0 при t = 0. Формулу (8.14) можно проинтерпретировать следующим образом: точка с постоянной насыщенностью движется с постоянной скоростью, пропорциональной v/m, и является функцией самой насыщенности. Для нахождения профиля водонасыщенности в любой момент времени необходимо ввести начальное и граничное условия. Например, если на входе в образец, изначально (t = 0) насыщенный нефтью с равномерно распределенной остаточной водонасыщенностью s0, закачивают только воду (F(s) = 1 в точке x = 0), то начальное и граничное условия примут вид:
Как видно из рисунка 29, одному и тому же значению Такая многозначность решения снимается, если ввести скачок насыщенности, положение которого определяется из условия материального баланса на скачке.
  б) б) 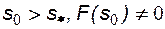
Тогда можно определить значение насыщенности на фронте вытеснения (на скачке) из соотношения:
Уравнение имеет простую геометрическую интерпретацию – уравнение касательной, проведенной из точки (s0, F (s0)) к кривой F (s), где sф – абсцисса точки касания, рис.29. Скорость фронта вытеснения, с учетом (8.14) при x0 =0, определяется из соотношения
Определить среднюю водонасыщенность за фронтом вытеснения (в зоне совместного течения воды и нефти) в безводный период добычи (на выход из образца или на выходное сечение пласта поступает одна только нефть), определяемую как отношение объема воды, содержащейся в пласте к моменту времени t, к объему порового пространства в зоне смеси, можно из соотношения:
Графически Определить время прорыва воды (момент появления воды на выходе из образца или на выходном сечении пласта) можно из решения уравнения (8.14) при x0 =0, положив х = L (L – длина образца или пласта) и s = sф:
Одним из важнейших параметров разработки нефтяных месторождений является коэффициент нефтеотдачи пласта. Коэффициент нефтеотдачи - отношение количества извлеченной из пласта нефти к первоначальным ее запасам в пласте. Различают текущую и конечную нефтеотдачу. Под текущей нефтеотдачей понимают отношение количества извлеченной из пласта нефти на данный момент разработки пласта к первоначальным ее запасам. Ее величина переменна во времени и возрастает по мере увеличения количества извлеченной из пласта нефти. Конечная нефтеотдача - отношение количества добытой нефти к первоначальным ее запасам в конце разработки пласта. Нефтеотдача вообще зависит от многих факторов. Обычно выделяют факторы, связанные с самим механизмом извлечения нефти из пластов, и факторы, характеризующие полноту вовлечения пласта в целом в разработку. Коэффициент текущей нефтеотдачи пластов
где:
В некоторых случаях коэффициент нефтеотдачи равен произведению не только двух, но и трех и большего числа коэффициентов:
где: Для плоскопараллельного случая, когда пласт однороден с постоянным распределением насыщенности по всей его длине и разрабатывается одной добывающей и одной нагнетательной цепочками скважин (а также при анализе результатов лабораторных экспериментов) при определении коэффициента нефтеотдачи можно не учитывать коэффициенты охвата и заводнения, приняв их равными 1.
Тогда коэффициент вытеснения за безводный период определяют по формуле:
Задачи к разделу 8
Задача 8.1 Построить функцию Бакли-Леверетта при вытеснении нефти водой с соотношением вязкостей
Определить значение насыщенности на фронте
Задача 8.2 Определить положение фронта вытеснения нефти водой в плоско- параллельном случае в различные моменты времени (1ч, 12 ч, 1 сут, 2сут, 5 сут, 10 сут), если пористость пласта m = 20%, ширина фильтрационного потока B = 500м, мощность пласта h = 10м, дебит галереи Q = 21600 м3/сут, а по экспериментальным данным снята зависимость функции Бакли-Леверетта F от водонасыщенности s:
Задача 8.3 Даны зависимости относительных фазовых проницаемостей воды Вязкость нефти μн = 7 мПа∙с, вязкость воды μв = 1 мПа∙с, остаточная водонасыщенность s0 = 0,2, остаточная нефтенасыщенность sност =
Задача 8.4 Даны зависимости относительных фазовых проницаемостей воды
Задача 8.5 Даны зависимости относительных фазовых проницаемостей воды Вязкость нефти μн = 7 мПа∙с, вязкость воды μв = 1 мПа∙с, остаточная водонасыщенность s0 = 0,3, конечная водонасыщенность при вытеснении нефти водой
Список литературы
1. Евдокимова В.А., Кочина И.Н. Сборник задач по подземной гидромеханике. - М.: Недра, 1979, 168 с. 2. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика. Учебник для вузов. - М.: Недра, 1993. 3. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебное пособие для вузов. - М.-Ижевск: Институт компьютерных исследований, 2005. 4. Телков А.П. Подземная гидрогазодинамика. – Уфимский нефтяной институт, Уфа, 1974. 5. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. - М.: Недра, 1984.
6. Щелкачев В.Н., Лanyк Б.Б. Подземная гидравлика. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. 7. Чарный И.А. Подземная гидрогазодинамика. - М.: Гостоптехиздат, 1963. 8. Ентов В.М., Зазовский А.Ф. Гидродинамика процессов повышения нефтеотдачи. - М.: Недра, 1989. 9. Маскет М. Течение однородных жидкостей в пористой среде. - М.-Ижевск: Институт компьютерных исследований, 2004. 10.Желтов Ю.П. Разработка нефтяных месторождений: Учебник для вузов.- М.:Недра, 1986.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.239.195 (0.053 с.) |
 , (8.1)
, (8.1) , (8.2)
, (8.2) ,
,  , (8.3)
, (8.3) ;
; ;
; , (8.4)
, (8.4) (8.5)
(8.5) (8.6)
(8.6) или
или  . (8.7)
. (8.7) и нефти
и нефти  подчиняются закону Дарси, который записывается для каждой из жидкостей отдельно:
подчиняются закону Дарси, который записывается для каждой из жидкостей отдельно: , (8.8)
, (8.8) . (8.9)
. (8.9) ,
,  - коэффициенты динамической вязкости соответственно воды и нефти, k – абсолютная проницаемость (определяемая по какой либо одной из жидкостей или газу), а
- коэффициенты динамической вязкости соответственно воды и нефти, k – абсолютная проницаемость (определяемая по какой либо одной из жидкостей или газу), а  и
и  - относительные фазовые проницаемости воды и нефти, характеризующие долю проводимости среды для соответствующей фазы при данной насыщенности.
- относительные фазовые проницаемости воды и нефти, характеризующие долю проводимости среды для соответствующей фазы при данной насыщенности. характеризует фазовую проницаемость i -ой жидкости
характеризует фазовую проницаемость i -ой жидкости  , как проницаемость в обычном смысле (абсолютную) только в условиях совместной фильтрации.
, как проницаемость в обычном смысле (абсолютную) только в условиях совместной фильтрации.


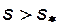 , где
, где  - называют насыщенностью связанной водой (или коэффициентом водоудерживающей способности). Следует понимать, что величина остаточной водонасыщенности
- называют насыщенностью связанной водой (или коэффициентом водоудерживающей способности). Следует понимать, что величина остаточной водонасыщенности  (начальное содержание воды в пласте) зачастую отличается от величины насыщенности связанной водой. Это связано с особенностями формирования реальных нефтенасыщенных пластов. Величина
(начальное содержание воды в пласте) зачастую отличается от величины насыщенности связанной водой. Это связано с особенностями формирования реальных нефтенасыщенных пластов. Величина 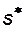 - конечная насыщенность водой, при которой нефть неподвижна, т.е. фильтруется только вода. Величина
- конечная насыщенность водой, при которой нефть неподвижна, т.е. фильтруется только вода. Величина 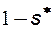 называется остаточной нефтенасыщенностью, или количество остаточной нефти, которое не может быть вытеснено из пористой среды водой, сколь бы длительным не было вытеснение. Таким образом, совместное течение двух фаз имеет место лишь в следующем интервале изменения насыщенности водой:
называется остаточной нефтенасыщенностью, или количество остаточной нефти, которое не может быть вытеснено из пористой среды водой, сколь бы длительным не было вытеснение. Таким образом, совместное течение двух фаз имеет место лишь в следующем интервале изменения насыщенности водой: . (8.10)
. (8.10) имеет значение, меньше 1, тогда как величина
имеет значение, меньше 1, тогда как величина  близка к единице. Это означает, что присутствие связанной смачивающей фазы мало влияет на течение несмачивающей жидкости (нефти), тогда как присутствие остаточной нефти значительно «стесняет» движение воды.
близка к единице. Это означает, что присутствие связанной смачивающей фазы мало влияет на течение несмачивающей жидкости (нефти), тогда как присутствие остаточной нефти значительно «стесняет» движение воды. , (8.11)
, (8.11) , а F(s) – функция насыщенности, называемая функцией распределения потоков Бакли - Леверетта.
, а F(s) – функция насыщенности, называемая функцией распределения потоков Бакли - Леверетта. . (8.12)
. (8.12) . (8.13)
. (8.13) - производная функции Бакли-Леверетта по s, рис.29.
- производная функции Бакли-Леверетта по s, рис.29. , (8.14)
, (8.14) (8.15)
(8.15)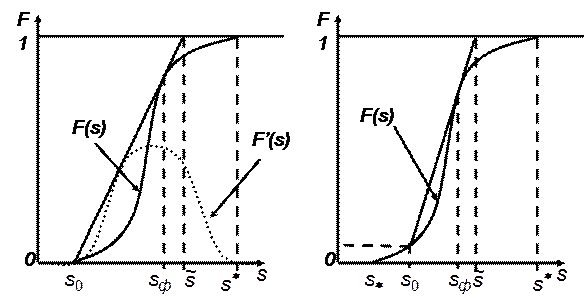
 . (8.16)
. (8.16) . (8.17)
. (8.17)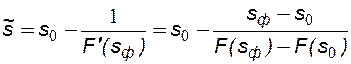 . (8.18)
. (8.18) можно определить по точке пересечения касательной к кривой F (s), определяющей фронтальную насыщенность, с прямой F (s)=1.
можно определить по точке пересечения касательной к кривой F (s), определяющей фронтальную насыщенность, с прямой F (s)=1.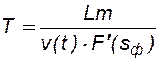 . (8.19)
. (8.19) при их разработке с применением заводнения представляют в виде следующего произведения:
при их разработке с применением заводнения представляют в виде следующего произведения: (8.20)
(8.20) - объем добытой из пласта нефти за определенный период времени,
- объем добытой из пласта нефти за определенный период времени,  - общий объем геологических запасов нефти,
- общий объем геологических запасов нефти,  - объем запасов нефти, охваченных заводнением.
- объем запасов нефти, охваченных заводнением. - коэффициент вытеснения нефти из пласта – величина, равная отношению количества вытесненной из пласта нефти к запасам нефти, первоначально находившимся в части пласта, вовлеченной в разработку. Отметим, что для текущей нефтеотдачи коэффициент вытеснения величина переменная во времени.
- коэффициент вытеснения нефти из пласта – величина, равная отношению количества вытесненной из пласта нефти к запасам нефти, первоначально находившимся в части пласта, вовлеченной в разработку. Отметим, что для текущей нефтеотдачи коэффициент вытеснения величина переменная во времени. - коэффициент охвата пласта разработкой – величина, равная отношению запасов нефти, вовлеченных в разработку, к общим геологическим запасам нефти в пласте.
- коэффициент охвата пласта разработкой – величина, равная отношению запасов нефти, вовлеченных в разработку, к общим геологическим запасам нефти в пласте.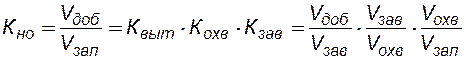 (8.21)
(8.21) - первоначальный объем нефти в заводненной области пласта, а
- первоначальный объем нефти в заводненной области пласта, а  - коэффициент заводнения – отношение объема нефти, в охваченной заводнением области пласта к первоначальным запасам в этой области.
- коэффициент заводнения – отношение объема нефти, в охваченной заводнением области пласта к первоначальным запасам в этой области.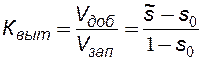 . (8.22)
. (8.22)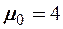 по следующим экспериментальным данным об относительных фазовых проницаемостях:
по следующим экспериментальным данным об относительных фазовых проницаемостях:

 и среднюю насыщенность порового пространства водой в зоне вытеснения
и среднюю насыщенность порового пространства водой в зоне вытеснения  .
.
 и нефти
и нефти  от водонасыщенности s. Построить распределение водонасыщенности в полосообразном пласте при t = 0,5сут. Определить коэффициент вытеснения нефти, среднюю водонасыщенность в момент прорыва воды к нагнетательным скважинам и время прорыва.
от водонасыщенности s. Построить распределение водонасыщенности в полосообразном пласте при t = 0,5сут. Определить коэффициент вытеснения нефти, среднюю водонасыщенность в момент прорыва воды к нагнетательным скважинам и время прорыва.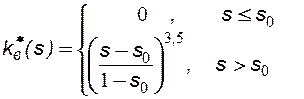



 =0,75.
=0,75.




