Моделирование случайных чисел распределенных равномерно в интервале (0,1).

Используется метод вычетов.

x_i+1={Ax_i}

A – некоторый множитель подбираем для компьютера исходя из размера сетки и влияет на качество получаемых чисел.

{} – функция модуля, т.е. мы отбрасываем целую часть и рассматриваем только дробную.

 

Рассмотрим графики этой функции при разных значениях А. Случайные числа находятся на этих графиках, но положение этих чисел в пределах графика случайно:

x_i+1 = f { x_i } А = 1 x_i+1 = { 2 x_i } А = 2 x_i+1 = { A x_i } A>>1

2

 

1 1 1

 

0 1 x_i 0 1 2 x_i 0 1 x_i

случайные числа заполняют квадрат плохо, неравномерно

заполнение более равномерное, т.е. качество этой последовательности выше.

 

j (x)

 

0 0,1 0,2 0,3 0,4... 1 x

 

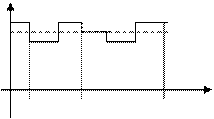
Если построить гистограмму полученной последовательности псевдослучайных чисел, то она будет иметь примерно такой вид. Отклонения от равномерного распределения будут тем меньше, чем больше длина последовательности и выше ее качество.

Моделирование случайных чисел, распределенных по равномерному закону в произвольном интервале (a,b).

 

Равномерное распределение в произвольном интервале (a,b) получается на основе равномерного распределения в интервале (0,1) путем преобразования по формуле:

x_(a,b) = a + (b – a) x_(0,1) ;

Характеристики этой последовательности:

Mx_(a,b) = (b + a) / 2; M – математическое ожидание

Dx_(a,b) = (b – a)² / 12; D – дисперсия

s = ÖD = (b – a) / 2 Ö 3; s – квадратичное отклонение

 

 

j (x)

 

0 1 x a a+1 b

 

 

Среднее значение 0.5

сдвиг на а и изменение длины интервала до значения (b-a) среднее значение (a+b)/2

 

Моделирование случайных чисел, распределенных по нормальному закону (закону Гаусса).

Это моделирование основано на центральной предельной теореме теории вероятностей – теореме Чебышева: “Сумма большого числа случайных слагаемых, если ни одно из них не преобладает над другими, при неограниченном росте числа слагаемых стремится к нормальному закону распределения.”

_N

h_(0,N) = S x_{i (0,1)}, где h - число, распределенное по нормальному закону;

ⁱ⁼¹ x - число, распределенное по равномерному закону.

Проиллюстрируем переход от равномерного закона к нормальному:

 

j(x₁) j(x₂) j(x₁ + x₂)

для j(x₁+x₂+x₃)

0 0,1 0,2... 1 x₁ 0 1 x₂ 0 1 2 3 x₁ + x₂

 

При сложении двух случайных чисел из интервала (0,1) в сумме получаем значение 0 только при x₁ = x₂ = 0 и значение 2 только при x₁ = x₂ = 1, но зато сумма, равная 1, получается при многих комбинациях x₁ и x₂, например, 0,1 + 0,9; 0,2 + 0,8; 0,3 + 0,7 и т.д. Таким образом, в интервале (0,2) распределение неравномерное. Для двух чисел – это треугольное распределение. При N = 5,6,7 сумма будет распределена почти по нормальному закону, имеющему вид:

j (х) Нормальный закон Гаусса.

 

 

N/2 N х

 

7. Моделирование непрерывных случайных величин с произвольным законом распределению j(x)

Функция распределения F(x) и плотность вероятности j(x) связаны соотношением:

_x

F(x) = ò_-µ j(x) dx;

 

j(х) Эта площадь равна F(x) х₀

значению F(x₀) 1 F(x₀) = ò₀ j(x) dx

0 x₀ x 0 х₀ x

 

Существует три способа получения случайных чисел, распределенных по заданному закону j(x): способ Неймана, способ обратной функции и способ Бусленко.

 

7.1.Способ Неймана.

М

x₁

 

0 a x₂ b x

j(x)

 

Необходимо смоделировать случайные числа, распределенные позаконуj(х).

1) Отмечаем интервалы [a,b] и [0,M], где M – max j(x).

2) Моделируем точку со случайными координатами:

x_1(0,M), x_2(a,b); x₁ = M * x_(0,1); x₂ = (b – a) * x_(0,1) + a

3) Проверяем, лежит ли точка над j(х) или под j(х),

 

т.е. j(x₂)<> x₂? Если j(x₂) > x₁, то точка принимается, т.е. мы рассматриваем ее как распределенную по закону j(х). При j(x₂) < x₁ точка отбрасывается. Совокупность принятых точек будет распределена по закону j(х).

Действительно, принятие точки означает, что она соответствует моделируемому закону j(х). Чем больше значение j(х), тем большее количество точек будет принятым и наоборот. Следовательно, большим значениям j(х) будет соответствовать пропорционально большая плотность принятых точек на оси х, что и требуется для моделирования плотности вероятности.

 

Способ обратной функции.

Теорема об обратной функции: “Если некоторая случайная величина имеет плотность вероятности j(х), то случайная величина

_xi

F(x_i) = ò j(x) dx

^{- ¥}

будет распределена по равномерному закону в интервале [0,1] независимо от вида функции j(х). Графически это можно проиллюстрировать следующим образом:

1 F(x)

F(x_i)

j(x)

0 x_i x

равномерное _xi

распределение j(F(x_i)) òj(x) dx

^{- ¥}

Все значения F(x_i) равновероятны (распределены по равномерному закону)

На основе этой теоремы моделируем закон j(x):

1) Моделируем случайное число x_{i (0,1)} и рассматриваем его как x_{i (0,1)} = F(x_i).

2) Составляем интегральное уравнение:

_{x i}

x_{i (0,1)} = ò j(x) dx.

^{- ¥}

и решаем его относительно верхнего предела интегрирования x_i. В соответствии с теоремой об обратной функции числа x_i будут распределены по закону j(x).

Пример: Смоделируем j(х) = lе^-lх (показательный закон).

j(x) = le^-lx

x=DT

_{xi xi}

x_(0,1) = ò le^-lx dx; x_(0,1) = -e^-lx ½ = e^-lxi + 1; x_i = -1/l * ln (1 - x_(0,1)).

^{0 0}

Число x_i можно рассматривать как интервал между заявками.

Прежде чем рассматривать способ Бусленко, рассмотрим следующий вопрос.

 

Недостаток – невсегда можно решить интеграл.

Достоинства – мы получаем формулу при которой надо сформулировать только 1 случайное число и подвергнуть его преобразованию по этой формуле.