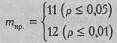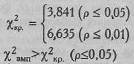Ограничения биномиального критерия

1. В выборке должно быть не менее 5 наблюдений. В принципе воз­можно применение критерия и при 2≤n<5, но лишь в отношении определенного типа задач (см. Табл. XV Приложения 1).

2. Верхний предел численности выборки зависит от ограничений, опре­деляемых пп.3-8 и варьирует в диапазоне от 50 до 300 наблюдений, что определяется имеющимися таблицами критических значений.

3. Биномиальный критерий m позволяет проверить лишь гипотезу о том, что частота встречаемости интересующего нас эффекта в обсле­дованной выборке превышает заданную вероятность Р. Заданная вероятность при этом должна быть: Р ≤0,50.

4. Если мы хотим проверить гипотезу о том, что частота встречаемости интересующего нас эффекта достоверно ниже заданной вероятности, то при Р=0,50 мы можем сделать это с помощью уже известного критерия знаков G, при Р>0,50 мы должны преобразовать гипоте­зы в противоположные, а при Р<0,50 придется использовать крите­рий χ².

По Табл. 5.12 легко определить, какой из путей для нас доступен.

Таблица 5.12

Выбор критерия для сопоставлений эмпирической частоты с теоретической при разных вероятностях исследуемого эффекта Р и разных гипотезах.

Заданные вероятности	H1: fэмпдостоверно выше f теор	H1: fэмп достоверно ниже fтеор
Р<0,50	А	m	для 2 ≤n ≤50	Б	χ^2	для n ≥30
Р=0,50	В	m	для 5 ≤n ≤300	Г	G	для 5 ≤n ≤300
Р>0,50	Д	χ^2	для n ≤30	Е	m	для 2 ≤n ≤50

Пояснения к Табл. 5.12

A) Если заданная вероятность Р<0,50, а f _эмп> f _теор (например, допус­тимый уровень брака - 15%, а в обследованной выборке получено значение в 25%), то биномиальный критерий применим для объема выборки 2≤n≤50.

Б) Если заданная вероятность Р<0,50, а f _эмп> f _теор (например, допус­тимый уровень брака - 15%, а в обследованной выборке наблюдает­ся 5% брака), то биномиальный критерий неприменим и следует применять критерий χ² (см. Пример 2).

B) Если заданная вероятность Р=0,50, а f _эмп> f _теор (например, вероят­ность выбора каждой из равновероятных альтернатив Р=0,50, а в обследованной выборке одна из альтернатив выбирается чаще, чем в половине случаев), то биномиальный критерий применим для объема выборки 5≤n≤300.

Г) Если заданная вероятность Р=0,50, a f _эмп> f _теор (например, вероят­ность выбора каждой из равновероятных альтернатив Р=0,50, а в обследованной выборке одна из альтернатив наблюдается реже, чем в половине случаев), то вместо биномиального критерия применяется критерий знаков G, являющийся "зеркальным отражением" биноми­ального критерия при Р=0,50. Допустимый объем выборки: 5≤n≤300.

Д) Если заданная вероятность Р>0,50, а f _эмп> f _теор (например, средне­статистический процент решения задачи - 80%, а в обследованной выборке он составляет 95%), то биномиальный критерий неприме­ним и следует применять критерий χ² (см. Пример 3).

Е) Если заданная вероятность Р>0,50, а f _эмп> f _теор (например, средне­статистический процент решения задачи - 80%, а в обследованной выборке он составляет 60%), то биномиальный критерий применим при условии, что в качестве "эффекта" мы будем рассматривать более редкое событие - неудачу в решении задачи, вероятность которого Q=l—Р=1—0,80=0,20 и процент встречаемости в данной выборке: 100%—75%=25%. Эти преобразования фактически сведут данную задачу к задаче, предусмотренной n. А. Допустимый объем выбор­ки: 2≤n≤50 (см. пример 3).

Пример 1

В процессе тренинга сенситивности в группе из 14 человек вы­полнялось упражнение "Психологический прогноз". Все участники должны были пристально вглядеться в одного и того же человека, ко­торый сам пожелал быть испытуемым в этом упражнении. Затем каж­дый из участников задавал испытуемому вопрос, предполагавший два заданных варианта ответа, например: "Что в тебе преобладает: отстра­ненная наблюдательность или включенная эмпатия?" "Продолжал бы ты работать или нет, если бы у тебя появилась материальная возмож­ность не работать?" "Кто тебя больше утомляет - люди нахальные или занудные?" и т. п. Испытуемый должен был лишь молча выслушать вопрос, ничего не отвечая. Во время этой паузы участники пытались определить, как он ответит на данный вопрос, и записывали свои про­гнозы. Затем ведущий предлагал испытуемому дать ответ на заданный вопрос. Теперь каждый участник мог определить, совпал ли его про­гноз с ответом испытуемого или нет. После того, как было задано 14 вопросов (13 участников + ведущий), каждый сообщил, сколько у него получилось точных прогнозов. В среднем было по 7-8 совпадений, но у одного из участников их было 12, и группа ему спонтанно зааплодиро­вала. У другого участника, однако, оказалось всего 4 совпадения, и он был очень этим огорчен.

Имела ли группа статистические основания для аплодисментов?

Имел ли огорченный участник статистические основания для грусти?

Начнем с первого вопроса.

По-видимому, группа будет иметь статистические основания для аплодисментов, если частота правильных прогнозов у участника А пре­высит теоретическую частоту случайных угадываний. Если бы участник прогнозировал ответ испытуемого случайным образом, то, в соответст­вии с теорией вероятностей, шансы случайно угадать или не угадать ответ на данный вопрос у него были бы равны P=Q=0,5. Определим теоретическую частоту правильных случайных угадываний:

f _теор=n· P

где n - количество прогнозов;

Р - вероятность правильного прогноза при случайном угадывании.

f _теор=14-0,5=7

Итак, нам нужно определить, "перевешивают" ли 12 реально данных правильных прогнозов 7 правильных прогнозов, которые могли бы быть у данного участника, если бы он прогнозировал ответ испы­туемого случайным образом.

Требования, предусмотренные ограничением 3, соблюдены: Р=0,50; f _эмп> f _теор. Данный случай относится к варианту "В" Табл. 5.12.

Мы можем сформулировать гипотезы.

H₀: Количество точных прогнозов у участника А не превышает часто­ты, соответствующей вероятности случайного угадывания.

H₁: Количество точных прогнозов у участника А превышает частоту, соответствующую вероятности случайного угадывания.

По Табл. XIV Приложения 1 определяем критические значения критерия m при n=14, Р=0,50:

Мы помним, что за эмпирическое значение критерия m принима­ется эмпирическая частота:

Зона значимости простирается вправо, в область более высоких значений m (более "весомых", если использовать аналогию с весами), а зона незначимости - в область более низких, "невесомых", значений m.

Ответ: H₀ отвергается. Принимается H₁. Количество точных прогнозов у участника А превышает (или по крайней мере равняется) критической частоте вероятности случайного угадывания (р≤0,01). Группа вполне обоснованно ему аплодировала!

Теперь попробуем ответить на второй вопрос задачи.

По-видимому, основания для грусти могут появиться, если коли­чество правильных прогнозов оказывается достоверно ниже теоретиче­ской частоты случайных угадываний. Мы должны определить, 4 точных прогноза участника Б - это достоверно меньше, чем 7 теоретически возможных правильных прогнозов при случайном угадывании или нет?

В данном случае Р=0,50; f _эмп> f _теор. В соответствии с ограничени­ем 4, в данном случае мы должны применить критерий знаков, кото­рый по существу является зеркальным отражением или "второй сторо­ной" одностороннего биномиального критерия (вариант "Г" Табл. 5.12). Вначале нам нужно определить, что является типичным событием для участника Б. Это неправильные прогнозы, их 10. Теперь мы опре­деляем, достаточно ли мало у него нетипичных правильных прогнозов, чтобы считать перевешивание неправильных прогнозов достоверным.

Сформулируем гипотезы.

H₀: Преобладание неправильных прогнозов у участника Б является случайным.

H₁: Преобладание неправильных прогнозов у участника Б не является случайным.

По Табл. V Приложения 1 определяем критические значения критерия знаков G для n=14:

Построим "ось значимости". Мы помним, что в критерии знаков зона значимости находится слева, а зона незначимости - справа, так как чем меньше нетипичных событий, тем типичные события являются бо­лее достоверно преобладающими.

Эмпирическое значение критерия G определяется как количество нетипичных событий. В данном случае:

Эмпирическое значение критерия G попадает в зону незначимости.

Ответ: H₀ принимается. Преобладание неправильных прогнозов у участника Б является случайным.

Участник Б не имел достаточных статистических оснований для огорчения. Дело, однако, в том, что психологическая "весомость" отклонения его оценки значительно перевешивает статистическую. Вся­кий практикующий психолог согласится, что повод для огорчения у уча­стника Б все же был.

Важная особенность биномиального критерия и критерия знаков состоит в том, что они превращают уникальность, единственность и жизненную резкость произошедшего события в нечто неотличимое от безликой и всепоглощающей случайности. Учитывая это, лучше исполь­зовать биномиальный критерий для решения более отвлеченных, форма­лизованных задач, например, для уравновешивания выборок по призна­ку пола, возраста, профессиональной принадлежности и т. п.

При оценке же личностно значимых событий оказывается, что статистическая сторона дела не совпадает с психологической больше, чем при использовании любого из других критериев.

Пример 2

В тренинге профессиональных наблюдателей допускается, чтобы наблюдатель ошибался в оценке возраста ребенка не более чем на 1 год в ту или иную сторону. Наблюдатель допускается к работе, если он совершает не более 15% ошибок, превышающих отклонение на 1 год. Наблюдатель Н допустил 1 ошибку в 50-ти попытках, а наблюдатель К - 15 ошибок в 50-ти попытках. Достоверно ли отличаются эти ре­зультаты от контрольной величины?

Определим частоту допустимых ошибок при п = 50:

f _теор=n· Р =50·0,15=7,5

Для наблюдателя Н f _эмп< f _теор. Для наблюдателя К f _эмп> f _теор

Сформулируем гипотезы для наблюдателя Н.

H₀: Количество ошибок у наблюдателя Н не меньше, чем это преду­смотрено заданной величиной.

H₁: Количество ошибок у наблюдателя Н меньше, чем это предусмот­рено заданной величиной.

В данном случае Р=0,15<0,50; f _эмп> f _теор.

Этот случай попадает под вариант Б Табл. 5. 12. Нам придется применить критерий у}, сопоставляя полученные эмпирические частоты ошибочных и правильных ответов с теоретическими частотами, состав­ляющими, соответственно, 7,5 для ошибочного ответа и (50-7,5)=42,5 для правильного ответа. Подсчитаем χ² по формуле, включающей по­правку на непрерывность[24]:

По Табл. IX Приложения 1 определяем критические значения χ² при v =l:

Ответ: H₀ отвергается. Количество ошибок у наблюдателя Н меньше, чем это предусмотрено заданной величиной (р≤0,05)

Сформулируем гипотезы для наблюдателя К.

H₀: Количество ошибок у наблюдателя К не больше, чем это преду­смотрено заданной величиной.

H₁: Количество ошибок у наблюдателя К больше, чем это предусмот­рено заданной величиной.

В данном случае Р=0,15<0,5; f _эмп> f _теор.Этот случай подпадает под вариант А Табл. 5.12. Мы можем применить биномиальный крите­рий, поскольку n=50.

По Табл. XV Приложения 1 определяем критические значения при п=50, Р=0,15, Q=0,85:

Ответ: H₀ отвергается. Количество ошибок у наблюдателя Н меньше, чем это предусмотрено заданной величиной (р<0,05).

Пример 3

Впримере 1 параграфа 5.2 мы сравнивали процент справившихся с экспериментальной задачей испытуемых в двух группах. Теперь мы можем сопоставить процент успешности каждой группы со среднестати­стическим процентом успешности. Данные представлены в Табл. 5.13.

Таблица 5.13

Показатели успешности решения задачи в двух группах испытуемых

	Количество испытуемых, решивших задачу	Количество испытуемых, не решивших задачу	Суммы
1 группа (n1=20)		(60%)		(40%)
2 группа (п7=25)		(40%)		(60%)
Суммы

Среднестатистический показатель успешности в решении этой за­дачи - 55%. Определим теоретическую частоту правильных ответов для групп 1 и 2:

Для группы 1, следовательно, Р=0,55>0,50; f _эмп=12> f _теор. Этот случай соответствует варианту "Д" Табл. 5.12. Мы должны были бы применить критерий χ², но у нас всего 20 наблюдений: n<30. Ни би­номиальный критерий, ни критерий χ² неприменимы. Остается крите­рий φ* Фишера, который мы сможем применить, если узнаем, сколько испытуемых было в выборке, по которой определялся среднестатистиче­ский процент.

Далее, для группы 2: Р=0,55>0,50; f _эмп=10> f _теор. Этот случай соответствует варианту "Е" Табл. 5.12. Мы можем применить биноми­альный критерий, если будем считать "эффектом" неудачу в решении задачи. Вероятность неудачи Q=l—Р=1—0,55=0,45. Новая эмпириче­ская частота составит: f _эмп=25-10=15.

Сформулируем гипотезы.

H₀: Процент неудач в обследованной выборке не превышает заданного процента неудач.

H₁ Процент неудач в обследованной выборке превышает заданный процент неудач.

По Табл. XV Приложения 1 определяем критические значения для n=25, P=0,45, Q=0.55 (мы помним, что Р и Q поменялись местами):

Ответ: H₀ принимается. Процент неудач в обследованной вы­борке не превышает заданного процента неудач.

Сформулируем общий алгоритм применения критерия m.

АЛГОРИТМ 18