Оптика. Атомная и ядерная физика.
Примеры решения задач
Задача №1
Определить число штрихов на 1 мм дифракционной решетки, если при нормальном падении света длиной волны l=600 нм решетка дает первый максимум на расстоянии l =3,3 см от центрального. Расстояние от решетки до экрана L=110 см (см.рисунок 10)).
 Дано: Решение: Дано: Решение:
l=600 нм=6×10-7 м Число штрихов N на 1 мм решетки
l =3,3 см=3,3×10-2 м определим по формуле:
L=110 см=1,1 м.  , (1) , (1)
______________________ где d - период решетки, т. е. расстояние между
 штрихами решетки. Период решетки найдем из штрихами решетки. Период решетки найдем из
формулы условия максимума:
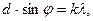 (2) (2)
где k - порядок (номер) максимума.

Рисунок 10
Ввиду того, что для максимума 1-го порядка угол мал, можно принять
 (3) (3)
Подставив в формулу (2) выражение синуса угла из (3), определим постоянную решетки
 (4) (4)
С учетом (4) формула (1) примет вид
 (5) (5)
Выпишем числовые значения, выразив их в СИ, и подставим в (5):
Для величин: l =3,3 см=3,3×10-2 м; L=110 см=1,10 м; k=1;
l=600 нм=600×10-9 м = 6×10-7 м;
 м-1=50000 м-1=50 мм-1. м-1=50000 м-1=50 мм-1.
Задача №2
На плоскопараллельную стеклянную пластинку ( =1,5) толщиной =1,5) толщиной  =5 см падает под углом =5 см падает под углом  =30 =30  луч света. Определить боковое смещение луча, прошедшего сквозь эту пластинку. луч света. Определить боковое смещение луча, прошедшего сквозь эту пластинку.
 Дано: Решение: Дано: Решение:
 =1,5 Согласно закону преломления: =1,5 Согласно закону преломления:
d =5 см=5×10-2 м  , (1) , (1)
 =30 =30  где где  - угол падения, - угол падения,  - угол преломления, - угол преломления,
______________________  - показатель преломления стекла. - показатель преломления стекла.
 Из (1), выразим Из (1), выразим  : :
 . (2) . (2)

Рисунок 11
Из рисунка 11, следует:
 , (3) , (3)
где  , ,  , ,  . .

где было учтено (2) и формула приведения 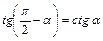 , откуда с учетом (3): , откуда с учетом (3):
 . .
Задача №3
Черное тело находится при температуре  . При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на . При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на  мкм. Определите температуру мкм. Определите температуру  , до которой тело охладилось. , до которой тело охладилось.
 Дано: Решение: Дано: Решение:
 Согласно закону смещения Вина: Согласно закону смещения Вина:  мкм мкм  , ,  , (1) , (1)
  , (2) , (2)
______________________
 откуда из (1) и (2), получим откуда из (1) и (2), получим
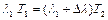 , ,

Задача №4
Калий освещается монохроматическим светом с длиной волны  . Определите наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна . Определите наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна  . .
 Дано: Решение: Дано: Решение:
 Согласно закону Эйнштейна для Согласно закону Эйнштейна для 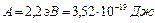 фотоэффекта: фотоэффекта:
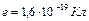  , ,
 где где
__________________________  - частота света. - частота света.
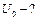 Задерживающее напряжение: Задерживающее напряжение:
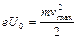 , ,  , ,

Задача №5
Определите потенциал ионизации атома водорода.
 Дано: Решение: Дано: Решение:
 Согласно формуле Бальмера: Согласно формуле Бальмера:
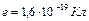 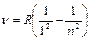 , ,
 где где  -частота спектральной линии; -частота спектральной линии;
_____________________ 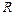 - постоянная Ридберга. - постоянная Ридберга.
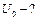 В случае, когда атом водорода ионизируется, В случае, когда атом водорода ионизируется,  . Потенциал ионизации определяется выражением: . Потенциал ионизации определяется выражением:
 , ,
откуда
 . .
Задача №6
Электрон находится в одномерной прямоугольной «потенциальной яме» шириной  с бесконечно высокими «стенками». Определите вероятность с бесконечно высокими «стенками». Определите вероятность  обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n=3). обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n=3).
 Дано: Решение: Дано: Решение:
 Согласно условию задачи электрону Согласно условию задачи электрону
 соответствует волновая функция: соответствует волновая функция:
 
_____________________ Вероятность обнаружения электрона в
 средней трети ямы определяется выражением: средней трети ямы определяется выражением:

Таким образом,

Вероятность обнаружения электрона в средней трети ямы равна  . .
Таблица 3. Варианты заданий РГР и контрольной работы №3
(в первой строке указаны последняя цифра, а в первом столбце
предпоследняя цифра зачетной книжки)
| Пред-послед-няя цифра
|
Последняя цифра шифра
1 2 3 4 5 6 7 8 9 0
|
| |
| 15.1
15.22
16.1
16.22
18.1
19.1
20.1
21.1
22.1
23.1
| 15.2
15.23
16.2
16.23
18.2
19.2
20.2
21.2
22.2
23.2
| 15.3
15.24
16.3
16.24
18.3
19.3
20.3
21.3
22.3
23.3
| 15.4
15.25
16.4
16.25
18.4
19.4
20.4
21.4
22.4
23.4
| 15.5
15.26
16.5
16.26
18.5
19.5
20.5
21.5
22.5
23.5
| 15.6
15.27
16.6
16.27
18.6
19.6
20.6
21.6
22.6
23.6
| 15.7
15.28
16.7
16.28
18.7
19.7
20.7
21.7
22.7
23.7
| 15.8
15.29
16.8
16.29
18.8
19.8
20.8
21.8
22.8
23.8
| 15.9
15.30
16.9
16.30
18.9
19.9
20.9
21.9
22.9
23.9
| 15.10
15.31
16.10
16.31
18.10
19.10
20.10
21.10
22.10
23.10
|
| |
| 15.11
15.32
16.11
16.32
18.11
19.11
20.11
21.11
22.11
23.11
| 15.12
15.33
16.12
16.33
18.12
19.12
20.12
21.12
22.12
23.12
| 15.13
15.34
16.13
16.34
18.13
19.13
20.13
21.13
22.13
23.13
| 15.14
15.35
16.14
16.35
18.14
19.14
20.14
21.14
22.14
23.14
| 15.15
15.36
16.15
16.36
18.15
19.15
20.15
21.15
22.15
23.15
| 15.16
15.37
16.16
16.37
18.16
19.16
20.16
21.16
22.16
23.16
| 15.17
15.38
16.17
16.38
18.17
19.17
20.17
21.17
22.17
23.17
| 15.18
15.39
16.18
16.39
18.18
19.18
20.18
21.18
22.18
23.18
| 15.19
15.40
16.19
16.40
18.19
19.19
20.19
21.19
22.19
23.19
| 15.20
15.41
16.20
16.41
18.20
19.20
20.20
21.20
22.20
23.20
| |
| 15.21
15.42
16.21
16.42
18.21
19.21
20.21
21.21
22.21
23.21
| 15.22
15.43
16.22
16.43
18.22
19.22
20.22
21.22
22.22
23.22
| 15.23
15.44
16.23
16.44
18.23
19.23
20.23
21.23
22.23
23.23
| 15.24
15.45
16.24
16.45
18.1
19.24
20.24
21.24
22.24
23.24
| 15.25
15.46
16.25
16.46
18.2
19.25
20.25
21.25
22.25
23.25
| 15.26
15.47
16.26
16.47
18.3
19.26
20.26
21.26
22.26
23.26
| 15.27
15.48
16.27
16.48
18.4
19.27
20.27
21.27
22.27
23.27
| 15.28
15.49
16.28
16.49
18.5
19.28
20.28
21.28
22.28
23.28
| 15.29
15.50
16.29
16.50
18.6
19.29
20.29
21.29
22.29
23.29
| 15.1
15.30
16.2
16.30
18.7
19.30
20.30
21.30
22.30
23.4
| |
| 15.2
15.31
16.3
16.31
18.8
19.31
20.31
21.31
22.31
23.5
| 15.3
15.32
16.4
16.32
18.9
19.32
20.32
21.32
22.32
23.6
| 15.2
15.33
16.5
16.33
18.10
19.33
20.33
21.33
22.33
23.7
| 15.3
15.34
16.6
16.34
18.11
19.34
20.34
21.34
22.34
23.8
| 15.4
15.35
16.7
16.35
18.12
19.35
20.35
21.35
22.35
23.9
| 15.5
15.36
16.8
16.36
18.13
19.36
20.36
21.36
22.36
23.10
| 15.6
15.37
16.9
16.37
18.14
19.37
20.37
21.2
22.37
23.11
| 15.7
15.38
16.10
16.38
18.15
19.38
20.38
21.3
22.38
23.12
| 15.8
15.39
16.11
16.39
18.16
19.39
20.39
21.4
22.39
23.13
| 15.9
15.40
16.12
16.40
18.17
19.40
20.40
21.5
22.40
23.14
| | | | | | | | | | | | | | | |
Окончание таблицы №3
|
| 15.10
15.41
16.13
16.41
18.18
19.41
20.41
21.6
22.41
23.15
| 15.11
15.42
16.14
16.42
18.19
19.3
20.42
21.7
22.42
23.16
| 15.12
15.43
16.15
16.43
18.20
19.4
20.1
21.8
22.43
23.17
| 15.13
15.44
16.16
16.44
18.21
19.5
20.2
21.9
22.5
23.18
| 15.14
15.45
16.17
16.45
18.22
19.6
20.3
21.10
22.6
23.19
| 15.15
15.46
16.18
16.46
18.23
19.7
20.4
21.11
22.7
23.20
| 15.16
15.47
16.18
16.47
18.1
19.8
20.5
21.12
22.8
23.21
| 15.17
15.48
16.19
16.48
18.2
19.9
20.6
21.13
22.9
23.22
| 15.18
15.49
16.20
16.49
18.3
19.10
20.7
21.14
22.10
23.23
| 15.19
15.50
16.21
16.50
18.4
19.11
20.8
21.15
22.11
23.24
| |
| 15.1
15.20
16.2
16.23
18.5
19.12
20.9
21.16
22.12
23.25
| 15.2
15.21
16.3
16.24
18.6
19.13
20.10
21.17
22.13
23.26
| 15.3
15.22
16.4
16.25
18.7
19.14
20.11
21.18
22.14
23.27
| 15.4
15.23
16.5
16.26
18.8
19.15
20.12
21.19
22.15
23.28
| 15.5
15.24
16.6
16.27
18.9
19.16
20.13
21.20
22.16
23.29
| 15.6
15.25
16.7
16.28
18.10
19.17
20.14
21.21
22.17
23.2
| 15.7
15.26
16.8
16.29
18.11
19.18
20.15
21.22
22.18
23.3
| 15.8
15.27
16.9
16.30
18.12
19.19
20.16
21.23
22.19
23.4
| 15.9
15.28
16.10
16.31
18.13
19.20
20.17
21.24
22.20
23.5
| 15.10
15.29
16.11
16.32
18.14
19.21
20.18
21.25
22.21
23.6
| |
| 15.11
15.30
16.12
16.33
18.15
19.22
20.19
21.26
22.22
23.7
| 15.12
15.31
16.13
16.34
18.16
19.23
20.20
21.27
22.23
23.8
| 15.13
15.32
16.14
16.35
18.17
19.24
20.21
21.28
22.24
23.9
| 15.14
15.33
16.15
16.36
18.18
19.25
20.22
21.29
22.25
23.10
| 15.15
15.34
16.16
16.37
18.19
19.26
20.23
21.30
22.26
23.11
| 15.16
15.35
16.17
16.38
18.20
19.27
20.24
21.31
22.27
23.12
| 15.17
15.36
16.18
16.39
18.21
19.28
20.25
21.32
22.28
23.13
| 15.18
15.37
16.19
16.40
18.21
19.29
20.26
21.33
22.29
23.14
| 15.19
15.38
16.20
16.41
18.22
19.30
20.27
21.34
22.30
23.15
| 15.20
15.39
16.21
16.42
18.23
19.31
20.28
21.35
22.31
23.16
|
| |
| 15.21
15.40
16.22
16.43
18.4
19.32
20.29
21.36
22.32
23.17
| 15.22
15.41
16.23
16.44
18.5
19.33
20.30
21.7
22.33
23.18
| 15.23
15.42
16.24
16.45
18.6
19.34
20.32
21.8
22.34
23.19
| 15.24
15.43
16.25
16.46
18.7
19.35
20.33
21.9
22.35
23.20
| 15.25
15.44
16.26
16.47
18.8
19.36
20.34
21.10
22.36
23.21
| 15.26
15.45
16.27
16.48
18.9
19.37
20.35
21.11
22.37
23.22
| 15.27
15.46
16.28
16.49
18.10
19.38
20.36
21.12
22.38
23.23
| 15.28
15.47
16.29
16.50
18.11
19.39
20.37
21.13
22.39
23.24
| 15.29
15.48
16.30
16.51
18.12
19.40
20.38
21.14
22.40
23.25
| 15.30
15.49
16.31
16.52
18.13
19.41
20.39
21.15
22.41
23.26
| |
| 15.31
15.50
16.32
16.53
18.14
19.5
20.40
21.16
22.42
23.27
| 15.1
15.32
16.33
16.54
18.15
19.6
20.41
21.17
22.43
23.28
| 15.2
15.33
16.34
16.55
18.16
19.7
20.42
21.18
22.1
23.29
| 15.3
15.34
16.35
16.56
18.17
19.8
20.1
21.19
22.2
23.4
| 15.4
15.35
16.36
16.57
18.18
19.9
20.2
21.20
22.3
23.5
| 15.5
15.36
16.37
16.58
18.19
19.10
20.3
21.21
22.4
23.6
| 15.6
15.37
16.38
16.59
18.20
19.11
20.4
21.22
22.5
23.7
| 15.7
15.38
16.39
16.60
18.21
19.12
20.5
21.23
22.6
23.8
| 15.8
15.39
16.40
16.61
18.22
19.13
20.6
21.24
22.7
23.9
| 15.9
15.40
16.41
16.62
18.23
19.14
20.7
21.25
22.8
23.10
| |
| 15.10
15.41
16.42
16.63
18.4
19.15
20.8
21.26
22.9
23.11
| 15.11
15.42
16.43
16.64
18.5
19.16
20.9
21.27
22.10
23.12
| 15.12
15.43
16.44
16.65
18.6
19.17
20.10
21.28
22.11
23.13
| 15.13
15.44
16.45
16.66
18.7
19.18
20.11
21.29
22.12
23.14
| 15.14
15.45
16.46
16.67
18.8
19.20
20.12
21.30
22.13
23.15
| 15.15
15.46
16.47
16.68
18.9
19.21
20.13
21.31
22.14
23.16
| 15.16
15.47
16.31
16.48
18.10
19.22
20.14
21.32
22.15
23.17
| 15.17
15.48
16.32
16.49
18.11
19.23
20.15
21.33
22.16
23.18
| 15.18
15.49
16.33
16.50
18.12
19.24
20.16
21.34
22.17
23.19
| 15.19
15.50
16.1
16.24
18.13
19.25
20.17
21.35
22.18
23.20
| | | | | | | | | | | | | | |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Стандарт организации. СТО 0493582-003-2006. – Уфа, 2006. – 32 с.
2. Волькенштейн В.С. Сборник задач по общему курсу физики. –СПб.: Книжный мир, 2007.-328с.
Лицензия РБ на издательскую деятельность № от года.
Подписано в печать _______________20 г. Формат 60х84. Бумага типографская. Гарнитура Таймс. Усл. печ. л. ________________. Усл. изд. л. ___________________. Тираж ________________ экз. Заказ № __________________.
Издательство Башкирского государственного аграрного университета.
Типография Башкирского государственного аграрного университета.
Адрес издательства и типографии: 450001, г. Уфа, ул. 50 лет Октября, 34.
|



 Дано: Решение:
Дано: Решение: , (1)
, (1) штрихами решетки. Период решетки найдем из
штрихами решетки. Период решетки найдем из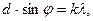 (2)
(2)
 (3)
(3) (4)
(4) (5)
(5) м-1=50000 м-1=50 мм-1.
м-1=50000 м-1=50 мм-1. =1,5) толщиной
=1,5) толщиной  =5 см падает под углом
=5 см падает под углом  =30
=30  луч света. Определить боковое смещение луча, прошедшего сквозь эту пластинку.
луч света. Определить боковое смещение луча, прошедшего сквозь эту пластинку. Дано: Решение:
Дано: Решение: , (1)
, (1) - угол преломления,
- угол преломления, Из (1), выразим
Из (1), выразим  . (2)
. (2)
 , (3)
, (3) ,
,  ,
,  .
.
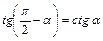 , откуда с учетом (3):
, откуда с учетом (3): .
. . При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на
. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на  мкм. Определите температуру
мкм. Определите температуру  , до которой тело охладилось.
, до которой тело охладилось. ,
,  , (1)
, (1)
 , (2)
, (2) откуда из (1) и (2), получим
откуда из (1) и (2), получим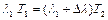 ,
,
 . Определите наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна
. Определите наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна  .
. Дано: Решение:
Дано: Решение: Согласно закону Эйнштейна для
Согласно закону Эйнштейна для 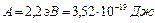 фотоэффекта:
фотоэффекта: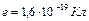
 ,
, где
где - частота света.
- частота света.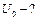 Задерживающее напряжение:
Задерживающее напряжение: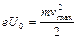 ,
,  ,
,
 Дано: Решение:
Дано: Решение: Согласно формуле Бальмера:
Согласно формуле Бальмера: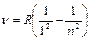 ,
, -частота спектральной линии;
-частота спектральной линии;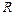 - постоянная Ридберга.
- постоянная Ридберга. . Потенциал ионизации определяется выражением:
. Потенциал ионизации определяется выражением: ,
, .
. с бесконечно высокими «стенками». Определите вероятность
с бесконечно высокими «стенками». Определите вероятность  обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n=3).
обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n=3). Дано: Решение:
Дано: Решение: Согласно условию задачи электрону
Согласно условию задачи электрону соответствует волновая функция:
соответствует волновая функция:

 средней трети ямы определяется выражением:
средней трети ямы определяется выражением:

 .
.


