
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 8 . Моделирование случайных величин и событий в MS Excel⇐ ПредыдущаяСтр 19 из 19
Моделирование простого события Пусть имеется событие A, вероятность наступления которого равна PA. Требуется разработать алгоритм, при многократном применении которого частота появления события стремилась бы к его вероятности. Процедура моделирования простого события описывается алгоритмом, показанным на рис.1. Оператор 1 обращается к датчику случайных чисел (ДСЧ), генерирующему случайную величину z в интервале [0, 1]. Оператор 2 проверяет условие z < PA. Если оно выполняется, считается, что произошло событие A (A=1), в противном случае считается, что произошло противоположное событие “не A” (A=0).
Рис.1. Блок-схема алгоритма моделирования простого события. В табличных моделях Excel ДСЧ в качестве, генерирующего случайное число в интервале [0, 1] с равномерным распределением, используется функция СЛЧИС(). Эта функция не имеет аргументов. Моделирование полной группы несовместимых событий Пусть имеется полная группа несовместимых событий A1, A2,…, Ak с вероятностями P1, P2, …, Pk. Для полной группы несовместимых событий выполняется условие нормировки:
Разделим интервал [0, 1] на k отрезков, длины которых составляют P1, P2, …, Pk соответственно. Если случайное число, генерируемое датчиком случайных чисел с равномерным распределением в интервале [0, 1], попало, например, на участок Pi, то это должно означать, что произошло событие i (i = 1..k). Процедура моделирования полной группы несовместимых событий описывается алгоритмом, блок-схема которого показана на рис.2. Оператор 1 обращается к датчику случайных чисел (ДСЧ), генерирующему случайную величину z в интервале [0, 1]. Условный оператор 2 проверяет условие попадания случайной величины z в интервал [0, L1]. Если условие выполняется, то считается, что произошло событие A1. Если условие в операторе 2 не выполняется, то алгоритм последовательно осуществляет проверку условий попадания случайной величины в другие интервалы.
Рис.2. Блок-схема алгоритма моделирования полной группы Дискретные случайные величины Дискретной случайной величиной называют случайную величину, которая принимает счетное число возможных значений xk (k = 1, 2, …) с заданной вероятностью pk каждое: P{X=xk} = pk Законом распределения дискретной случайной величины X называют соответствие между ее возможными значениями и их вероятностями. Закон распределения дискретной случайной величины можно задать табличным, аналитическим и графическим способами.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит список ее возможных значений xk, а вторая строка таблицы – их вероятности pk:
причем Примером аналитического задания дискретной случайной величины является, например, биномиальный закон распределения вероятностей:
где X принимает целочисленные значения k, Pn(k) – вероятность наступления ровно k событий в n независимых испытаниях, Интегральная функция распределения дискретной случайной величины X в общем случае имеет вид:
Из этой формулы, в частности, следует, что F(xk+0) - F(xk) = pk т.е. функция распределения дискретной случайной величины испытывает скачки в точках xk, для которых существует положительная вероятность события {X = xk}. На рис.3, 4 показаны примеры графического представления функции распределения дискретной случайной величины с законом распределения, заданным следующей таблицей:
Рис.3. Полигон распределения вероятностей дискретной случайной величины.
Рис.4. Интегральная функция распределения дискретной случайной величины. Видим, что функция распределения имеет скачки в тех точках, в которых случайная величина принимает ненулевые значения согласно ряду распределения, а величина скачка равна вероятности этого значения. Сумма величин всех скачков функции распределения равна 1. Очевидно, что по значениям интегральной функции распределения дискретной случайной величины можно легко восстановить ее ряд распределения. Скачкообразное поведение функции распределения в точках X=xk с учетом условия нормировки позволяет разработать простой алгоритм моделирования произвольной дискретной случайной величины с помощью датчика случайных чисел, равномерно распределенных на отрезке [0, 1].
Моделирование дискретной случайной величины Дискретная случайная величина может быть задана табличной зависимостью:
Здесь pj – вероятность того, что дискретная величина X примет значение xj. При этом выполняется условие нормировки p1 + p2 + … +pn = 1. Разделим интервал [0, 1] на n отрезков, длины которых пропорциональны вероятностям pi. Если случайное число z, вырабатываемое датчиком случайных чисел, равномерно распределенных в интервале [0, 1], попадет в интервал pj, то случайная величина X примет значение xj. Таким образом, при моделировании дискретных случайных величин фактически используется та же процедура, что и при моделировании полной группы несовместимых событий. Непрерывные случайные величины Непрерывной случайной величиной называют случайную величину, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Плотностью распределения вероятностей f(x) непрерывной случайной величины называют первую производную от интегральной функции распределения: f(x) = F’(x). По определению функции f(x) вероятность того, что непрерывная случайная величина X получит значение, принадлежащее интервалу [a, b], равна:
Зная плотность вероятностей f(x), можно найти интегральную функцию распределения вероятностей:
Плотность распределения вероятностей непрерывной случайной величины обладает следующими свойствами: 1. Плотность распределения вероятностей неотрицательна: f(x) ³ 0. 2. Несобственный интеграл от плотности распределения вероятностей в пределах Моделирование непрерывной случайной величины Пусть имеется некоторая непрерывная случайная величина x, заданная интегральной функцией распределения F(x). Можно доказать, что значения этой функции равномерно распределены и интервале [0, 1]. Поэтому между случайной величиной z, равномерно распределенной в этом интервале, и функцией распределения исходной случайной величины x существует взаимно однозначное соответствие, т.е. z = F(x) (1) Отсюда следует, что x = F-1(z) (2) где F-1 - обратная функция. Следовательно, если уравнение (2) имеет аналитическое решение, то для моделирования случайной величины x можно использовать датчик случайных чисел, генерирующий случайную величину z, и затем найти соответствующее значение x по формуле (2).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 809; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.29.145 (0.008 с.) |



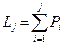 .
. . Данная таблица называется рядом распределения.
. Данная таблица называется рядом распределения.
 - число сочетаний из n по k.
- число сочетаний из n по k.




 . В частности, если все возможные значения случайной величины принадлежат интервалу [a, b], то
. В частности, если все возможные значения случайной величины принадлежат интервалу [a, b], то  .
.


