Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение размеров частиц в дисперсной системе методом непрерывного взвешивания.Содержание книги
Поиск на нашем сайте
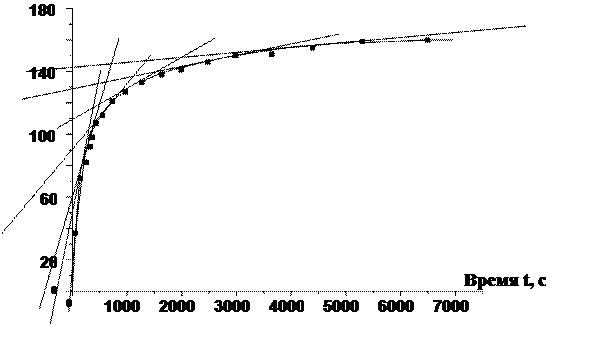
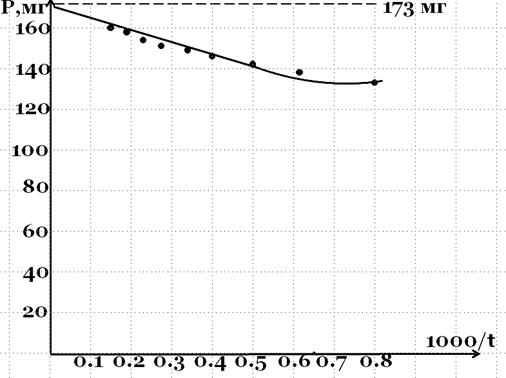
Рис.VI.8 Для нахождения предела, к которому стремится седиментационная кривая, строят 7 - 10 первых точек в координатах Р = f (А/t), где А = 1000 и экстраполируют полученную прямую на ось ординат. Точка пересечения соответствует величине Pmax, т.к. при t → ∞, A/t→ 0. Из полученной седиментационной кривой можно рассчитать процентное соотношение отдельных фракций частиц в суспензии. Для этого выбирают несколько точек (обычно 10 – 15) на кривой, соответствующих временам оседания t1, t2, t3, t4 и т.д. и проводят касательные в каждой точке. Уравнение касательной в любой точке кривой седиментации имеет вид: P = Pi + (dP/dt) * ti, где dP/dt – тангенс угла наклона касательной (это уравнение Одена). Процесс седиментации монодисперсной системы, (где все частицы одного размера), графически выражался бы прямой линией, а процесс седиментации полидисперсной системы, как в нашем случае, можно представить в виде плавной кривой, состоящей из множества бесконечно малых прямых участков. Поэтому каждая касательная к кривой седиментации отсекает от оси ординат отрезок, равный весу частиц, полностью осевших к данному моменту времени. Так, касательной, проходящей через точку А, соответствует вес частиц Р1 и время оседания t1(tmin); касательной, проходящей через точку В, соответствует вес частиц Р2 и время оседания t2 и т.д. Для каждого времени оседания можно рассчитать эквивалентный радиус частиц по формуле (IV.8), преобразовав её для удобства в виде:
h0 – глубина погружения чашечки в суспензию, см; t -время оседания частиц, с. Если воспользоваться указанными формулами, подставив в них вязкость воды η = 0,01 пз; ускорение свободного падения g – 981 cм/ с2; а плотности (ρ1 – ρ0) выразить в г/см3, то с учетом переводного множителя 104, величина r будет выражена в мкм (микронах). Отношение Р1/Рmax соответствует процентному содержанию частиц первой, самой крупной фракции, с размером частиц от rmax до r1 (величину rmax сообщает преподаватель); отношение Р2/ Рmax соответствует содержанию частиц следующей фракции, с размером частиц от r1 до r2 и т.д. Эти отношения легче всего получить, измерив длины отрезков ординаты между касательными и выразив их в процентах от общей длины ординаты, соответствующей пределу седиментационной кривой (Рmax). Полученные данные записывают в таблицу (VI.2).
Таблица (VI.2).
На основании данных таблицы (VI.2) строят суммарную кривую распределения: откладывают по оси ординат суммарное процентное содержание фракций Q, начиная с самых мелких частиц; по оси абсцисс откладывают радиусы частиц, соответствующие большему значению интервала радиусов данной фракции. Например, если в исследуемом порошке самая мелкая фракция имела радиусы меньше 2,6 мкм, а её количество составило 17,5%, то по оси абсцисс откладывают величину 2,6 мкм, а по оси ординат – 17,5%. Следующая фракция находится в пределах 2,6 – 3,2 мкм, и её количество равно 8,2%, тогда по оси абсцисс откладывают величину 3,2 мкм, а по оси ординат сумму 17,5 + 8,2 = 23,7%и т.д.Полученный график называется интегральной кривой распределения. Естественно, на этом графике отложены не целочисленные значения радиусов частиц, а радиусы, соответствующие тем временам седиментации, которые мы выбрали при проведении опыта. При переходе от интегральной к дифференциальной кривой распределения ось абсцисс разбивают на равные интервалы радиусов, обычно этот интервал выбирают в 2 мкм (хотя бы для первых пяти точек), и находят величины приращения процентного содержания частиц ∆ Q /∆ r для каждого интервала; после чего заполняют таблицу (VI.3): Таблица (VI.3).
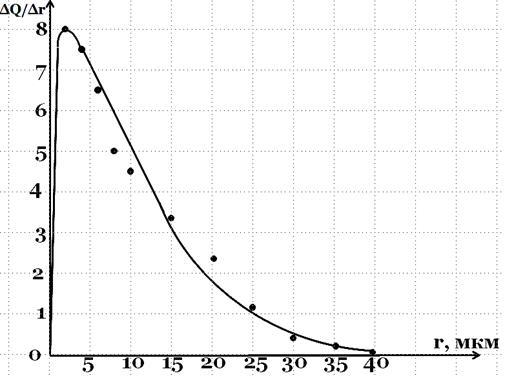
По данным таблицы (VI.3) строят дифференциальную кривую распределения, откладывая по оси ординат значения ∆Q/∆r, а по оси абсцисс – значения радиусов R. Каждый интервал радиусов частиц можно построить в виде прямоугольников: первый - шириной от 2 до 4 мкм, высотой 2,5; следующий – шириной 4-6 мкм, высотой 5,0 и так до максимального радиуса частиц. Затем соединяют середины прямоугольников и получают плавную кривую с одним максимумом, соответствующим наиболее вероятному размеру частиц основной фракции. Впрочем, у полидисперсной системы вполне может оказаться дифференциальная кривая с двумя максимумами.
Образец оформления протокола по этой работе.
Лабораторная работа: «Седиментационный анализ методом непрерывного взвешивания осадка» Выполнил студент ….. группы ……курса ………….….факультета Фамилия ………… Имя……………….
Вес чашечки в воде 133 мг, глубина погружения h0 = 11.2 см.; вязкость 0,01пз. Плотность: частиц дисперсной фазы 2,5 г/см3; дисперсионной среды 1,0 г/см3;
Таблица 1 (VI.1)
Седиментационная кривая.
Таблица 3 (VI.3).
Лабораторная работа №3 “Применение уравнения Фрейндлиха к адсорбции Таблица №1
Формула для расчета: Vк-тыNк-ты = VNaOHNNaOH; т.к. С NaOH = 0.108, то Сисходн. к-ты = (34.8*0.1080)/10 = 0.3683 моль/л. Путём последовательного разбавления исходной задачи с концентрацией кислоты 0,3683 моль/л вдвое приготовим ещё 5 растворов с концентрациями: 1) 0,1842 моль/л; 2) 0,0921 моль/л; 3) 0,0460 моль/л; 4) 0,0230 моль/л; 5) 0,0115 моль/л К каждому из этих шести растворов добавим по 1 г угля и оставим на 1 час. (Это время целесообразно использовать для титрования исходного раствора кислоты.) Затем отфильтруем уголь, а фильтраты употребим для титрования по три порции каждая по 10 мл всё тем же раствором щёлочи (С NaOH = 0,108 моль/л). Результаты титрования поместим в Таблицу №2
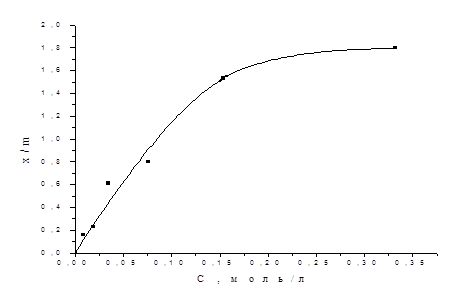
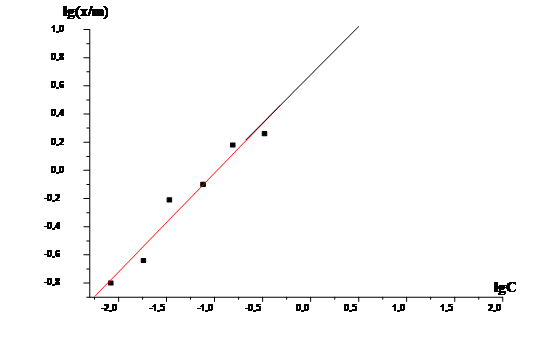
Расчет величин x/m проводят по формуле (IX.11), которая с учетом массы адсорбента в 1г, объема раствора 50мл и коэффициента перевода концентрации в ммоль/л, равного 1000, выглядит как: (IX.12) x/m = (с0 –сх)* 50 Результаты расчётов поместим в Таблицу №3
Изотерма адсорбции
Таблица 1. Результаты эксперимента
Рис. X.20. Зависимость концентрации раствора в средней камере от количества прошедшего электричества.
Кажущийся выход по току может быть вычислен на основании изменений концентрации электролита в средней камере и суммарного количества прошедшего электричества по формуле: (Со – Скон)[ моль/л]*V[ л ]*96500 Кл ηкаж = _______________________________________________________________ I [A]*[ c ] Q = I [A]*t [ c ] - количество прошедшего электричества в А*c; V- объём раствора в л; Сo и Скон - концентрации иона до и после электродиализа в моль/л Для данных приведенных в таблице №1 ηкаж = 40,3% Лабораторная работа №5. Таблица 1. Набухание желатины в KBr.
Таблица 2. Набухание желатины в воде
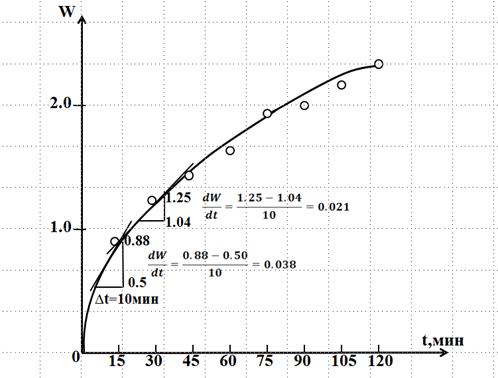
По полученным данным строят два графика в координатах: степень набухания W от времени набухания t [ мин.] (мы в качестве примера приводим только один график зависимости W от t для набухания желатины в воде (рис.XI.5). После того как данные из таблицы 2 нанесены на график (рис.XI.5,), проводят усредненную плавную кривую из начала координат. Процесс набухания протекает как реакция первого порядка: dW/dt = A(W∞ - W), где: А – постоянная, зависящая от природы полимера; W – степень набухания; W∞ - предельная степень набухания; dW/dt – скорость набухания.
Рис.XIV.5 Можно представить это уравнение в виде W = W∞ − (1/А) * dW/dt (это уравнение прямой, не проходящей через начало координат), с помощью которого можно найти графически предельную степень набухания W∞ и константу А. Для этого необходимо построить график зависимости степени набухания W от скорости набухания dW/dt. Для построения такого графика на кривой (рис. XIV.5) выбирают точки, соответствующие времени набухания 15, 30, 45, 60, 75, 90, 105 мин., и в каждой из этих точек проводят касательную к кривой W = f(t). Используя эту касательную, как гипотенузу, строят треугольники, в каждом из которых катет, соответствующий оси времени, составляет 10 мин. и вычисляют ряд значений ΔW и dW/dt, как это показано на рис .XIV.5.
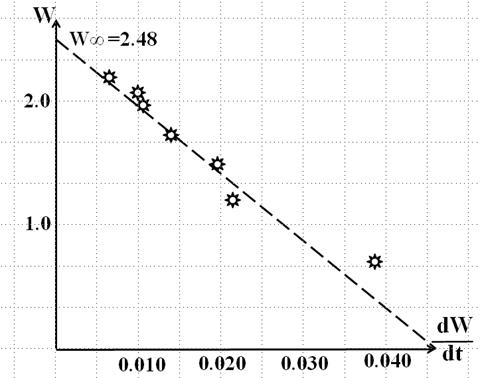
Затем заполняют таблицу 3 и по её данным строят график зависимости степени набухания W от скорости набухания dW/dt (рис.XIV.6). Таблица 3.
По этим точкам (на рис. XIV.6 – звёздочки) проводят усредненную прямую, причем экстраполяция этой прямой на ось ординат (dW/dt = 0), даст значение W∞; а на ось абсцисс (W = 0), даст величину A*W∞ . После этого вычисляют значение А..
Рис.XIV.6 В нашем случае: W∞ = 2,48; А = 0, 0185.
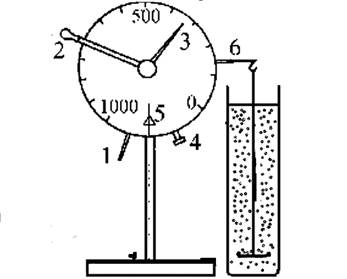
Определение размеров частиц в дисперсной системе методом непрерывного взвешивания. Метод непрерывного взвешивания осадка заключается в измерении увеличения массы осадка в чашечке, опущенной в оседающую суспензию и связанной кварцевой нитью с торзионными весами (рис.VI.6,7)
В начале опыта в измерительный стакан наливают 1л дистиллированной воды и делают отметку её уровня на стенке стакана. После этого на торзионных весах взвешивают в воде кварцевую нить с прикрепленной к ней чашечкой из фольги (Р0) и определяют глубину её погружения в жидкость h0 (разность между верхним уровнем водыи положением чашечки). Для успешного проведения опыта оптимальный вариант величин Р0 составляет не более 100 – 150 мг, а величин h0 от 8 до 12 см. Затем отбирают из этого стакана около 300 мл воды в промывочную колбу и готовят суспензию, взяв по указанию преподавателя навеску исследуемого порошка и растерев её в фарфоровой ступке с небольшим количеством воды до однородной массы.
(Рис.VI.6) (Рис.VI.7) Приготовленную смесь переносят в литровый стакан с оставшейся водой, остатки смеси аккуратно смывают водой из промывочной колбы, доведя уровень суспензии до первоначальной отметки, после чего суспензию в стакане тщательно перемешивают. Рекомендуется производить это перемешивание, поставив стакан в положение, удобное для последующих измерений, т.е. непосредственно под коромысло торзионных весов. Сразу же после прекращения перемешивания опускают в стакан кварцевую нить с чашечкой, противоположный конец этой нити подвешивают к весам и одновременно с выключением арретира весов включают секундомер, после чего стараются сделать первое измерение не позднее 30 с от начала оседания частиц. По мере накопления осадка на чашечке заполняют таблицу (VI.1), в которой отмечают вес осевших частиц и время наблюдения. Таблица (VI.1)
Рекомендуется заранее подготовить указанную таблицу для записи измерений, первые 3-4 замера сделать с интервалом в 30 с, затем по 3-4 замера с интервалом в 1мин., после чего увеличивать интервал между замерами до 2, 5, 10, 20 минут. На новый временной интервал целесообразно переходить тогда, когда вес частиц, осевших на чашечку в предыдущем измерении составит всего 1-2 мг. Опыт считается законченым, когда за 20 мин. на чашечке оседает 1-2 мг, что обычно происходит по прошествии примерно 2 часов. По полученным данным строят седиментационную кривую (рис.VI.8) в координатах P = f(t), где: Р – вес осевших частиц, мг; t – время седиментации, с.; Формат миллиметровой бумаги, рекомендуемый для построения седиментационной кривой, А3 или А4 (при этом, если потребуется, начальный участок можно построить в более крупном масштабе).
Рис.VI.8 Для нахождения предела, к которому стремится седиментационная кривая, строят 7 - 10 первых точек в координатах Р = f (А/t), где А = 1000 и экстраполируют полученную прямую на ось ординат. Точка пересечения соответствует величине Pmax, т.к. при t → ∞, A/t→ 0. Из полученной седиментационной кривой можно рассчитать процентное соотношение отдельных фракций частиц в суспензии. Для этого выбирают несколько точек (обычно 10 – 15) на кривой, соответствующих временам оседания t1, t2, t3, t4 и т.д. и проводят касательные в каждой точке. Уравнение касательной в любой точке кривой седиментации имеет вид: P = Pi + (dP/dt) * ti, где dP/dt – тангенс угла наклона касательной (это уравнение Одена). Процесс седиментации монодисперсной системы, (где все частицы одного размера), графически выражался бы прямой линией, а процесс седиментации полидисперсной системы, как в нашем случае, можно представить в виде плавной кривой, состоящей из множества бесконечно малых прямых участков. Поэтому каждая касательная к кривой седиментации отсекает от оси ординат отрезок, равный весу частиц, полностью осевших к данному моменту времени. Так, касательной, проходящей через точку А, соответствует вес частиц Р1 и время оседания t1(tmin); касательной, проходящей через точку В, соответствует вес частиц Р2 и время оседания t2 и т.д. Для каждого времени оседания можно рассчитать эквивалентный радиус частиц по формуле (IV.8), преобразовав её для удобства в виде:
h0 – глубина погружения чашечки в суспензию, см; t -время оседания частиц, с. Если воспользоваться указанными формулами, подставив в них вязкость воды η = 0,01 пз; ускорение свободного падения g – 981 cм/ с2; а плотности (ρ1 – ρ0) выразить в г/см3, то с учетом переводного множителя 104, величина r будет выражена в мкм (микронах). Отношение Р1/Рmax соответствует процентному содержанию частиц первой, самой крупной фракции, с размером частиц от rmax до r1 (величину rmax сообщает преподаватель); отношение Р2/ Рmax соответствует содержанию частиц следующей фракции, с размером частиц от r1 до r2 и т.д. Эти отношения легче всего получить, измерив длины отрезков ординаты между касательными и выразив их в процентах от общей длины ординаты, соответствующей пределу седиментационной кривой (Рmax). Полученные данные записывают в таблицу (VI.2). Таблица (VI.2).
На основании данных таблицы (VI.2) строят суммарную кривую распределения: откладывают по оси ординат суммарное процентное содержание фракций Q, начиная с самых мелких частиц; по оси абсцисс откладывают радиусы частиц, соответствующие большему значению интервала радиусов данной фракции. Например, если в исследуемом порошке самая мелкая фракция имела радиусы меньше 2,6 мкм, а её количество составило 17,5%, то по оси абсцисс откладывают величину 2,6 мкм, а по оси ординат – 17,5%. Следующая фракция находится в пределах 2,6 – 3,2 мкм, и её количество равно 8,2%, тогда по оси абсцисс откладывают величину 3,2 мкм, а по оси ординат сумму 17,5 + 8,2 = 23,7%и т.д.Полученный график называется интегральной кривой распределения. Естественно, на этом графике отложены не целочисленные значения радиусов частиц, а радиусы, соответствующие тем временам седиментации, которые мы выбрали при проведении опыта. При переходе от интегральной к дифференциальной кривой распределения ось абсцисс разбивают на равные интервалы радиусов, обычно этот интервал выбирают в 2 мкм (хотя бы для первых пяти точек), и находят величины приращения процентного содержания частиц ∆ Q /∆ r для каждого интервала; после чего заполняют таблицу (VI.3): Таблица (VI.3).
По данным таблицы (VI.3) строят дифференциальную кривую распределения, откладывая по оси ординат значения ∆Q/∆r, а по оси абсцисс – значения радиусов R. Каждый интервал радиусов частиц можно построить в виде прямоугольников: первый - шириной от 2 до 4 мкм, высотой 2,5; следующий – шириной 4-6 мкм, высотой 5,0 и так до максимального радиуса частиц. Затем соединяют середины прямоугольников и получают плавную кривую с одним максимумом, соответствующим наиболее вероятному размеру частиц основной фракции. Впрочем, у полидисперсной системы вполне может оказаться дифференциальная кривая с двумя максимумами.
Образец оформления протокола по этой работе.
Лабораторная работа: «Седиментационный анализ методом непрерывного взвешивания осадка» Выполнил студент ….. группы ……курса ………….….факультета Фамилия ………… Имя……………….
Вес чашечки в воде 133 мг, глубина погружения h0 = 11.2 см.; вязкость 0,01пз. Плотность: частиц дисперсной фазы 2,5 г/см3; дисперсионной среды 1,0 г/см3;
Таблица 1 (VI.1)
Седиментационная кривая.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.149.93 (0.014 с.) |

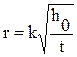 и рассчитав отдельно константу k:
и рассчитав отдельно константу k: 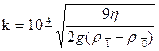 где:
где: