
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хвильові властивості частинокСодержание книги Поиск на нашем сайте
Мета роботи: вивчення хвильових властивостей мікрочастинок та експериментальне підтвердження хвильової природи електронів за допомогою ефекту Рамзауера. Прилади та обладнання: панель з тиратроном ТГ-3-0,1/1,3; випрямляч ВУП-2, гальванометр, вольтметр, джерело постійного струму 12 В, гальванічний елемент 1,5 В (наприклад елемент 045), реостат 200 Ом, з’єднувальні провідники.
Теоретичні відомості При розгляді еволюції фізичних моделей будови атома [1], відмічалось, що труднощі моделі атома Бора були усунуті завдяки квантовій фізиці. Як з’ясувалось, причиною недоліків теорії був погляд класичної фізики на те, що собою являє мікрочастинка (електрон, протон і т. п.). Так, наприклад, електрон представлявся як маленька механічна частинка з певним розміром, координатами, швидкістю і т. п. Вважалося, що він рухається в атомі за точно визначеною траєкторією – по коловій орбіті навколо ядра. Іншими словами, рівнянням руху був ІІ-й закон механіки, що доповнювався постулатами Бора. Те, що модель атома за Бором не змогла описати навіть атом з двома електронами (атом гелію), привело до висновку про те, що природа мікрочастинок та закони їх руху не такі, як стверджувала класична фізика. Рішенню останніх труднощів сприяли дослідження в іншому розділі фізики – в оптиці. За Ейнштейном природа світла двоїста (точніше, двоєдина): світло являє собою не лише електромагнітну хвилю, а й потік корпускул (частинок), названих в подальшому квантами (фотонами). Встановлення дуалізму “хвиля-частинка” дозволила в 1924 році французькому фізику Луї де-Бройлю висунути сміливу гіпотезу зворотного порядку про дуалізм “частинка-хвиля”, тобто що частинки мають не лише корпускулярну, а й хвильову природу. Таким чином, було висунуте припущення про універсальність корпускулярно-хвильового дуалізму: обидва види матерії – і речовина і поле, – кожен має двоїсту природу. Таким чином, оскільки фотон володіє енергією
та імпульсом
то і мікрочастинки, наприклад, електрон, також зв’язані з хвильовим процесом. Довжина хвилі частинки дорівнює
а частота
тобто співвідношення (1), (3) та (2), (4) являють собою одне і те ж. Проте, це незвичайні хвилі. Встановлений в подальшому фізичний зміст хвиль де-Бройля (їх статистичне тлумачення) говорить про те, що це ймовірнісні хвилі, оскільки квадрат модуля їх амплітуди визначає ймовірність місцезнаходження мікрочастинки в просторі. Гіпотеза де-Бройля згодом була підтверджена експериментально шляхом виявлення у мікрочастинок властивостей, характерних для хвильових процесів (дифракції). Це явище спостерігалось на специфічних дифракційних решітках – площинах, утворених атомами кристалічної решітки твердого тіла.
Розглянемо деякі найважливіші властивості хвиль де-Бройля і, перш за все, швидкість їх поширення. Як відомо, хвильовий процес характеризується (див., наприклад, [2], § 134) фазовою швидкістю
де Іншими словами, процес описується швидкістю переміщення певної фази хвильового фронту. Окрім даної характеристики хвилі притаманна і групова швидкість
тобто швидкість руху групи або цугу (низки) хвиль, яка за відсутності поглинання в середовищі збігається із швидкістю переміщення енергії цієї групи хвиль. Для хвиль де-Бройля із врахуванням значення хвильового числа і виразів (2) та (4) отримаємо
Оскільки за співвідношенням Ейнштейна
Оскільки c > v, то фазова швидкість хвиль де-Бройля
бентежити, оскільки Групова швидкість хвиль де-Бройля за (6)
Неважко довести, що Але за другим законом Ньютона
Тоді з (9) і (10) слідує, що
тобто групова швидкість хвиль де-Бройля дорівнює швидкості руху мікрочастинки. Існує ще одна властивість хвиль де-Бройля. В елементарній теорії воднеподібного атома зо Бором правило відбору стаціонарних кругових орбіт (або 1-й постулат Бора; див. [1], ст.27) має вигляд
Цю умову можна записати у вигляді
З формули (3) слідує, що
тобто довжина кола стаціонарної орбіти електрона в атомі повинна дорівнювати цілому числу хвиль де-Бройля.
Згідно з квантовою теорією для виконання умови (14) хвильова функція, яка описує рух електрона в атомі, повинна бути однозначною. Здійснення дослідів, які підтверджують хвильову природу мікрочастинок, не таке просте. Складність полягає перш за все в тому, що дослід, схема якого зображена на рис.1, повинен здійснюватись в достатньо високому вакуумі, який можна отримати не в будь-якій лабораторії. Проте підтвердження хвильової природи мікрочастинок можна здійснити й іншим способом, наприклад, за допомогою ефекту Рамзауера. Цей ефект, виявлений в 1921 році, посідає видатне місце серед дослідів, пояснення яких потребує врахування хвильової природи мікрочастинок. Виникає ефект Рамзауера при взаємодії (розсіянні) електронів з атомами важких інертних газів (
де З (15) випливає, що
Оскільки
і Із останнього виразу випливає фізичний зміст Згідно класичної теорії зі збільшенням швидкості (енергії) електронів Ефект Рамзауера: в області невеликих прискорюючих потенціалів (тобто, при малих значеннях енергії) електронів, відбувається як збільшення, так і зменшення ефективного перерізу Пояснення явища можливе тоді, коли прийнято, що електрони мають хвильову природу і має де-бройлівською довжиною хвилі
Така поведінка електронів пояснюється їх хвильовою природою: якщо довжина хвилі електрона стає співрозмірною з діаметром атома інертного газу, то відбувається умова дифракції – “електронна хвиля” огинає атом, і розсіяння електронів зменшується. Зменшується і ефективний переріз розсіяння Для перевірки того, що цей ефект (максимум струму тиратрону і мінімум ефективного перерізу) дійсно обумовлений зіткненнями з атомами Зміна довжини хвилі де-Бройля електрона обумовлена зміною прискорюючої напруги
Визначимо звідси швидкість електронів
і підставивши в (3), отримаємо вираз, що визначає залежність змін де-бройлівської довжини хвилі від прискорюючої напруги:
де
Правила техніки безпеки В роботі необхідно виконувати правила електробезпеки (розділ 1, §3).
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1054; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.008 с.) |

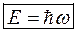
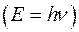 (1)
(1)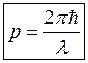
 , (2)
, (2)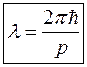
 , (3)
, (3)
 , (4)
, (4)



 Спочатку Девісон і Джермер спостерігали дифракційну картину при відбиванні пучка моноенергетичних електронів від шліфованої поверхні нікелю, що мав кристали кубічної форми. Потім в тому ж 1927 році Г.П.Томсон і незалежно від нього П.С.Тартаковський отримали дифракційну картину при проходженні електронного пучка через металеву фольгу (рис. 1). Прискорені різницею потенціалів порядку декількох десятків кіловольт, електрони дифрагували на кристалічній решітці фольги, утворюючи картину, представлену на рис. 2. Дифракційна картина за зовнішнім виглядом ідентична дифракційній картині при проходженні світла крізь дифракційну решітку.
Спочатку Девісон і Джермер спостерігали дифракційну картину при відбиванні пучка моноенергетичних електронів від шліфованої поверхні нікелю, що мав кристали кубічної форми. Потім в тому ж 1927 році Г.П.Томсон і незалежно від нього П.С.Тартаковський отримали дифракційну картину при проходженні електронного пучка через металеву фольгу (рис. 1). Прискорені різницею потенціалів порядку декількох десятків кіловольт, електрони дифрагували на кристалічній решітці фольги, утворюючи картину, представлену на рис. 2. Дифракційна картина за зовнішнім виглядом ідентична дифракційній картині при проходженні світла крізь дифракційну решітку. Штерн та його співробітники показали, що дифракційні явища виявляються також і в атомних, і в молекулярних пучках. Остаточні висновки були зроблені в 1949 році в досліді Л.М.Бібермана, К.Г.Сушкіна та В.А.Фабриканта. В ньому було продемонстровано, що дифракційна картина є не властивістю колективу мікрочастинок, а притаманна кожному окремому електрону.
Штерн та його співробітники показали, що дифракційні явища виявляються також і в атомних, і в молекулярних пучках. Остаточні висновки були зроблені в 1949 році в досліді Л.М.Бібермана, К.Г.Сушкіна та В.А.Фабриканта. В ньому було продемонстровано, що дифракційна картина є не властивістю колективу мікрочастинок, а притаманна кожному окремому електрону.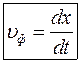 , або
, або  , або
, або 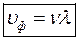 , (5)
, (5) та
та 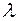 – відповідно, частота і довжина хвилі,
– відповідно, частота і довжина хвилі,  – хвильове число.
– хвильове число. , (6)
, (6) . (7)
. (7)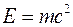 , то остаточно
, то остаточно , або
, або  . (8)
. (8) більша від швидкості світла с у вакуумі. Однак цей факт не повинен нас
більша від швидкості світла с у вакуумі. Однак цей факт не повинен нас . (9)
. (9)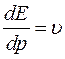 . Дійсно, зміна енергії під дією сили
. Дійсно, зміна енергії під дією сили  на шляху
на шляху 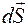 дорівнює
дорівнює  .
.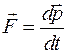 . Тому
. Тому 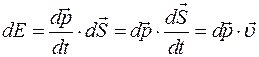 або так як
або так як  і
і 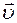 однаково напрямлені, то
однаково напрямлені, то  , звідки
, звідки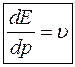 . (10)
. (10)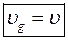 , (11)
, (11)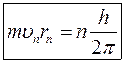 (n = 1; 2; 3;…). (12)
(n = 1; 2; 3;…). (12) . (13)
. (13)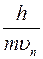 – довжина хвилі де-Бройля, тоді
– довжина хвилі де-Бройля, тоді , (14)
, (14)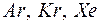 ). Тому, перш ніж виявляти суть явища, зупинимось на досить важливих характеристиках взаємодії мікрочастинок – перерізах розсіяння.
). Тому, перш ніж виявляти суть явища, зупинимось на досить важливих характеристиках взаємодії мікрочастинок – перерізах розсіяння.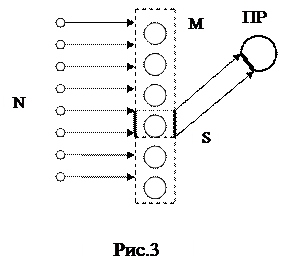 Нехай мішень М (рис. 3) – тонка металічна фольга. Товщина її дорівнює розмірам атома речовини мішені. Нехай із усіх
Нехай мішень М (рис. 3) – тонка металічна фольга. Товщина її дорівнює розмірам атома речовини мішені. Нехай із усіх 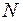 падаючих на фольгу частинок
падаючих на фольгу частинок 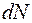 буде розсіяно в результаті взаємодії з атомами мішені. Кількість таких частинок буде відмічена реєстраційним приладом (РП). Тоді очевидно, що
буде розсіяно в результаті взаємодії з атомами мішені. Кількість таких частинок буде відмічена реєстраційним приладом (РП). Тоді очевидно, що 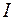 пучка падаючих частинок, тобто
пучка падаючих частинок, тобто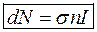 , (15)
, (15)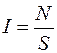 – кількість частинок, падаючих на одиницю площі поверхні мішені за одиницю часу;
– кількість частинок, падаючих на одиницю площі поверхні мішені за одиницю часу;  – коефіцієнт пропорційності.
– коефіцієнт пропорційності.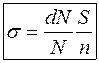 . (16)
. (16)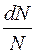 – відносна кількість розсіяних частинок – характеризує ймовірність взаємодії в даному випадку, тобто
– відносна кількість розсіяних частинок – характеризує ймовірність взаємодії в даному випадку, тобто 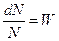 , тоді отримаємо
, тоді отримаємо (17)
(17) В даній роботі для експериментального доказу хвильової природи електронів використовується чіткий мінімум розсіяння електронів на атомах ксенону
В даній роботі для експериментального доказу хвильової природи електронів використовується чіткий мінімум розсіяння електронів на атомах ксенону  біля значень енергії 0,7 еВ. Тому дослід проводиться на тиратроні ТГ-3-0,1/1,3 – електронній лампі, наповненій криптон-ксеноновою сумішшю (див. електричну схему на рис. 5). Електрони, що емітують з катода К, під дією прискорюючого потенціалу
біля значень енергії 0,7 еВ. Тому дослід проводиться на тиратроні ТГ-3-0,1/1,3 – електронній лампі, наповненій криптон-ксеноновою сумішшю (див. електричну схему на рис. 5). Електрони, що емітують з катода К, під дією прискорюючого потенціалу 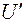 , прямують до анода А, розсіюючись при цьому на атомах ксенону
, прямують до анода А, розсіюючись при цьому на атомах ксенону 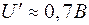
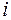 тиратрону в даному випадку найбільший (рис.4). при подальшому зростанні напруги, а, отже, і швидкості, і енергії електронів, струм зменшується.
тиратрону в даному випадку найбільший (рис.4). при подальшому зростанні напруги, а, отже, і швидкості, і енергії електронів, струм зменшується.


 іде на збільшення їх кінетичної енергії, а математично це має вигляд
іде на збільшення їх кінетичної енергії, а математично це має вигляд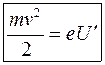 . (18)
. (18)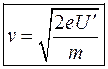 (19)
(19)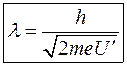 , (20)
, (20)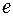 та
та  – відповідно, заряд і маса електрона.
– відповідно, заряд і маса електрона.


