
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перелік рисунків і таблиць звіту з даної роботиСодержание книги
Поиск на нашем сайте 1. Вольт-амперна характеристика газонаповненого іонізаційного лічильника (за рис. 1). 2. Схема будови лічильника Гейгера-Мюллера (за рис. 2). 3. Робоча схема (за рис. 4). 4. Графік лічильної характеристики для фону 5. Графіки 6. Таблицю виміряних і обчислених величин у довільній формі.
Контрольні запитання 1. Описати вольт-амперну характеристику газонаповненого іонізаційного лічильника.
2. Пояснити будову і принцип дії лічильника Гейгера-Мюллера. 3. Які існують способи гасіння розряду в лічильниках? 4. Які основні характеристики лічильника? 5. Яке іонізуюче випромінювання реєструє лічильник Гейгера? 6. Що таке фон і робочий фон лічильника? 7. Який фізичний зміст коефіцієнта поглинання? Література 1. И.В.Савельев, Курс общей физики, т.ІІ. – М.: Наука, 1973. 2. О.Ф.Кабардин. Практикум по ядерной физике. − М.: 1965. 3. Гольдина Л.Л. Практикум к лабораторным занятиям по общей физике. – М.: 1973. 4. П.Е.Колпаков. Основы ядерной физики. − М.: 1968. 5. И.В.Ракобольская. Ядерная физика. − М.: Изд-во МГУ, 1980.
Лабораторна робота №6 Розподіл Пуассона Мета роботи: експериментальне визначення графічного виразу розподілу Пуассона і його використання до обчислення статистичних похибок при вивченні вторинного космічного випромінювання. Прилади і обладнання: лічильник Гейгера-Мюллера з блоком живлення, перерахунковий прилад СІЛ-І і секундомір.
Теоретичні відомості В сучасній фізиці і, особливо, в атомній і ядерній часто проводяться такі вимірювання, результати яких представляються у вигляді не дуже великих цілих чисел. Так, наприклад, крізь лічильник іонізуючих частинок за час вимірювань проходить невелике скінченне ціле число мікрочастинок, або ядро, яке ділиться, може розпастися на ціле і невелике число частинок. Статистичні закономірності, які мають місце в цьому випадку, дещо відрізняються від вивчених раніше в таких розділах фізики, як механіка, молекулярна фізика, електродинаміка тощо. Відрізняються відповідно і правила обчислення похибок вимірювань. Для вивчення останніх зупинимося спочатку на основних уявленнях і поняттях теорії ймовірностей. Процеси, які відбуваються в атомі або його ядрі, мають ймовірнісний характер. Це поняття тісно пов’язане з існуючими в природі випадковими явищами (подіями) − явищами, які можуть відбутися або не відбутися. Такі явища поділяються на одиничні (які можуть відбутися принципово тільки один раз; наприклад, ядро атома може розпастися принципово тільки один раз), масові чи однорідні (які відбуваються з подібними об’єктами, або об’єктами, що повторюються, наприклад, розпад ядер шматка урану). Це значить, що одиничні явища відбуваються в малих, а однорідні у великих просторово-часових масштабах. Закономірності, яким підлягають лише однорідні явища, називаються статистичними. Щоб кількісно описати однорідні випадкові явища або події, вводиться поняття ймовірності W − границі відношення числа сприятливих (тобто потрібних нам) подій ni до повного (загального) числа подій N:
Ймовірність може бути визначена ще й іншим способом:
де t − час перебування системи в даному стані, тобто час спостерігання сприятливої події; T − повний час, протягом якого відбуваються явища такого типу. Іноді для ймовірнісного опису явищ досить поняття частоти повторень, тобто
або відносного числа подій даного роду. У фізиці випадкове явище або подія можуть полягати ще й у тому, що якийсь фізичний параметр буде мати випадкову величину. Ймовірності появи того чи іншого значення випадкової величини змінюються із зміною умов. Сукупність значень ймовірностей даної випадкової величини x, яка описує те чи інше явище (подію), утворює функцію розподілу ймовірностей або розподіл W(x). Серед найчастіше розподілів, які застосовуються виділяється розподіл Пуассона, що визначає ймовірність того, що дискретна випадкова величина x приймає будь-яке значення з нескінченого ряду значень:
де a − деяка постійна, яка є − середнім значенням випадкової величини x. В даному розподілі
Розподілу Пуассона задовольняє, наприклад: а) число ядер радіоактивного елемента, які розпадаються в одиницю часу; б) кількість молекул, які випаровуються з поверхні рідини за певний проміжок часу; в) число частинок, які проходять крізь лічильник Гейгера-Мюллера і т.п.
Граничним випадком розподілу Пуассона являється розподіл Гауса, який визначає ймовірність того чи іншого значення неперервної випадкової величини. Цей розподіл часто називають нормальним законом. В даній роботі йдеться про те, яким чином на прикладі проходження мікрочастинок крізь лічильник Гейгера-Мюллера можна експериментально одержати розподіл Пуассона. Джерелом частинок в лабораторії, як і в будь-якому приміщенні на нашій планеті, є вторинне космічне випромінювання, а також продукти розпаду радіоактивних речовин, які в дуже малих кількостях є всюди. Таке випромінювання називається радіоактивним фоном, до якого додається випромінювання радіоактивних джерел, які вивчаються. Число зареєстрованих лічильником частинок фону залежить від багатьох факторів (розмірів камери лічильника, тиску, складу газу, матеріалу стінок камери і т.п.). Але якщо досліди робити з одним і тим же лічильником, то всі вищевказані фактори будуть незмінними. Таким чином число зареєстрованих частинок буде визначатися часом дослідів. Але і в цьому випадку результат, одержаний в досліді, буде відрізнятися від дійсного значення внаслідок похибок, які складаються з: 1) систематичних похибок, обумовлених неточністю приладів і недосконалістю методик вимірювань; 2) випадкових похибок, що змінюють свою величину від досліду до досліду. Окремим випадком останніх являються статистичні похибки − похибки, обумовлені флуктуаціями (відхиленням від середнього значення) вимірювальної величини. До числа флуктуаційних величин відносяться, наприклад, інтенсивність космічного випромінювання − число частинок, які проходять через одиницю площі лічильника в одиницю часу:
Що значить флуктуація інтенсивності? Припустимо, що при вимірюванні за 10 секунд лічильником зареєстровано n космічних частинок. Але це не значить, що в будь-які 10 секунд буде зареєстровано знову n частинок. З випадкових причин
може бути n-1, n-2 або інше, взагалі, число, яке не дуже сильно відрізняється від n. В цьому і проявляється флуктуації числа частинок (інтенсивності космічного випромінювання). В даній роботі при невеликих розмірах лічильника і малому часі вимірювання (10 с) всі похибки стають зневажне малими порівняно із статистичними флуктуаціями, тому ніяких інших похибок крім статистичних можна не розглядати. Визначимо тепер дослідним шляхом вид розподілу Пуассона. Проведемо для цього ряд дослідів, вимірюючи число частинок в лічильнику Гейгера-Мюллера за фіксований час t. Кількість цих дослідів N повинно бути досить великим, тому що при визначенні ймовірності Порівнявши одержані результати, ми побачимо, що знайдені числа значно відрізняються одне від одного, хоча серед них зустрічаються і однакові. Побудуємо графік, відкладаючи по осі абсцис число частинок n, зареєстрованих протягом 10 с, а по осі ординат число дослідів, в яких зареєстроване це число, тобто
де n¢ − число дослідів, в яких зареєстроване дане число частинок n.
Тепер треба проаналізувати одержану функцію розподілу ймовірностей. Перш за все відмітимо, що вираз 6) являє собою
миттєву інтенсивність випромінювання − число частинок, які проходять через одиницю площі лічильника за одиницю часу в даний момент. Це величина, яка на практиці важко визначається. Більш доступною тут являється середня (хоча і взагалі невідома нам величина) інтенсивність. Позначимо її також n. Тоді середнє число nо частинок космічного випромінювання, які проходять через лічильник за час t, буде
Не дивлячись на те, що число відліків лічильника, виміряне за будь-який час, являється цілим числом, середнє не обов’язково повинно бути цілим. Відмітимо основні особливості розподілу Пуассона (рис. 1): 1) ні для якого n ймовірність 2) максимум розподілу приходиться на середнє значення; З) при менших проміжках часу графік залежності Аналітичний вираз розподілу Пуассона для подібних вимірювань буде мати вигляд:
В даній роботі повинні проводитися багаторазові досліди для вияснення достатньо точного вигляду функції W(n). Але насправді багаторазові досліди проводяться рідко. При цьому необхідно знати очікувану різницю результату одного вимірювання від істинного (дійсного) значення, тобто точність вимірювань. Для її оцінки застосовують величину, яка називається дисперсією. Дисперсією s2 випадкової величини називається середнє значення квадрата відхилення цієї величини від її середнього значення, тобто
Величина s − корінь квадратний з дисперсії, називається середньоквадратичним відхиленням або стандартною похибкою,
В теорії ймовірностей показано, що стандартна похибка числа відліків лічильника за деякий інтервал часу дорівнює кореню квадратному із середнього значення числа відліків:
Але дійсне значення вимірюваної величини завжди невідоме, інакше для визначення не потрібно було б ставити досліди. Тому в формулі (2) для визначення стандартної похибки окремого виміру доводиться підставляти не дійсне nо, а виміряне середнє значення
Формула (12) показує, що виміряне число відрізняється від шуканого середнього не більше, ніж на
Відносна ж стандартна похибка, яка показує відносну точність окремого вимірювання, дорівнює
Аналогічно відносна похибка по всіх значеннях у вимірюваннях дорівнює
або з урахуванням виразу (12)
Таким чином, відносна точність вимірювань середнього значення
Правила техніки безпеки При виконанні даної роботи необхідно виконати правила електробезпеки (див. §3 вступу).
|
||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.012 с.) |

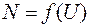 із вказівкою робочого фону і робочої напруги.
із вказівкою робочого фону і робочої напруги.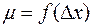 для свинцю і сталі (в одній системі координат).
для свинцю і сталі (в одній системі координат).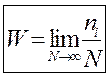 . (1)
. (1)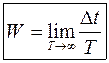 , (2)
, (2)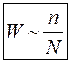 , (3)
, (3) , (4)
, (4) . (5)
. (5) . (6)
. (6) . В нашому досліді N повинно прямувати до якогось великого числа (приблизне визначення ймовірності) наприклад, N=400.
. В нашому досліді N повинно прямувати до якогось великого числа (приблизне визначення ймовірності) наприклад, N=400.
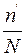 ,
,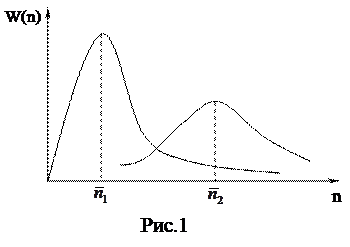 Побудований таким чином графік розподілу результатів досліду виявляє максимум в області шуканого середнього значення, хоча серед результатів знаходяться і такі, які дуже відрізняються від середнього. Очевидно, що частина випадків, в яких дане число частинок, виявляється,
Побудований таким чином графік розподілу результатів досліду виявляє максимум в області шуканого середнього значення, хоча серед результатів знаходяться і такі, які дуже відрізняються від середнього. Очевидно, що частина випадків, в яких дане число частинок, виявляється,  . (7)
. (7) ;
; має більш асиметричний вигляд; по мірі зростання проміжку часу максимум функції зсувається вправо і стає ширшим, а сам графік стає більш симетричним відносно точки
має більш асиметричний вигляд; по мірі зростання проміжку часу максимум функції зсувається вправо і стає ширшим, а сам графік стає більш симетричним відносно точки 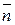 .
.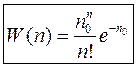 . (8)
. (8)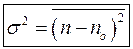 . (9)
. (9)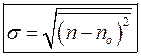 . (10)
. (10)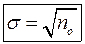 . (11)
. (11)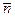 :
: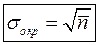 , (12)
, (12)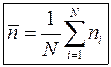 . (13)
. (13) :
: . (14)
. (14)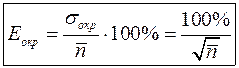 . (15)
. (15)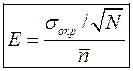 , (16)
, (16) . (17)
. (17)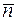 визначається тільки повним числом
визначається тільки повним числом 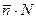 і не залежить від інтервалів розбиття серії (по 10, 20, 40, 100,... секунд).
і не залежить від інтервалів розбиття серії (по 10, 20, 40, 100,... секунд).


