
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель объемной реверберацииСодержание книги
Поиск на нашем сайте
Интенсивность объемной реверберации в изотропной среде может быть определена в соответствии со следующим выражением /1, 4/
где
Используя известную зависимость интенсивности звуковой энергии от эффективного значения акустического давления, для квадрата эффективного значения акустического давления, создаваемого объемной реверберацией можно записать следующее выражение
При работе ГБО на мелководье водную среду нельзя рассматривать как изотропную, так как при взаимодействии ветра с водной поверхностью происходит ее насыщение воздушными пузырьками, концентрация которых уменьшается с глубиной. Вследствие этого величина параметра Если воспользоваться приведенными в работе /1/ соотношениями, то, с учетом значительной ширины ХН антенны ГБО в вертикальной плоскости, для квадрата эффективного значения акустического давления, создаваемого объемной реверберацией от приповерхностного слоя, можно записать следующее выражение
где
Значение параметра
где
Значения параметров
Рисунок 4 Площадь
где
При разбиении импульсного объема на равные по высоте участки высоты всех параллелепипедов равны и, следовательно, параметр Ширина параллелепипеда зависит от дистанции до реверберирующего объема и ширины ХН антенны в горизонтальной плоскости и может быть определена из следующего выражения
где Используя выражения (43) и (44) и вынося постоянные члены за знак суммы, выражение (41) можно записать в следующем виде
П р и м е ч а н и е. При расчете результирующего сигнала на выходе антенны в соответствии с выражением (6) член
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.207.141 (0.008 с.) |

 , (39)
, (39)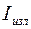 - интенсивность звука по оси характеристики направленности антенны на расстоянии 1 м от антенны;
- интенсивность звука по оси характеристики направленности антенны на расстоянии 1 м от антенны; - коэффициент обратного рассеяния, равный отношению интенсивности обратного рассеяния, создаваемого единичным объемом на расстоянии 1 м от него, к интенсивности падающей звуковой волны;
- коэффициент обратного рассеяния, равный отношению интенсивности обратного рассеяния, создаваемого единичным объемом на расстоянии 1 м от него, к интенсивности падающей звуковой волны; - импульсный объем, создающий реверберацию в текущий момент времени;
- импульсный объем, создающий реверберацию в текущий момент времени; - дистанция до центра импульсного объема
- дистанция до центра импульсного объема  . (40)
. (40) не является постоянной величиной и зависит от глубины, на которой находится рассеивающий объем. Объемную реверберацию в этом случае следует рассматривать как реверберацию от приповерхностного слоя. Модель подобного вида реверберации, учитывающая различный вклад отдельных частей импульсного объема, представлена в работе /1/.
не является постоянной величиной и зависит от глубины, на которой находится рассеивающий объем. Объемную реверберацию в этом случае следует рассматривать как реверберацию от приповерхностного слоя. Модель подобного вида реверберации, учитывающая различный вклад отдельных частей импульсного объема, представлена в работе /1/.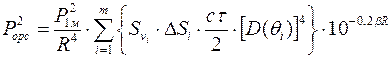 , (41)
, (41) - количество сечений импульсного объема по глубине;
- количество сечений импульсного объема по глубине; - значение коэффициента обратного рассеяния
- значение коэффициента обратного рассеяния  -ом горизонте;
-ом горизонте; - площадь вертикального сечения участка импульсного объема на
- площадь вертикального сечения участка импульсного объема на  - угол в вертикальной плоскости между осью ХН антенны ГБО и направлением на центр
- угол в вертикальной плоскости между осью ХН антенны ГБО и направлением на центр  , (42)
, (42) - значение параметра
- значение параметра  - крутизна спадания параметра
- крутизна спадания параметра  - глубина центра участка импульсного объема, м.
- глубина центра участка импульсного объема, м.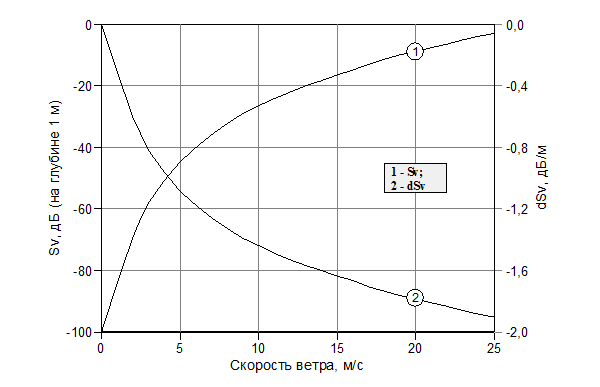
 , (43)
, (43)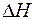 - высота параллелепипеда;
- высота параллелепипеда; - ширина параллелепипеда в плоскости касательной к волновому фронту.
- ширина параллелепипеда в плоскости касательной к волновому фронту.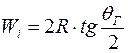 , (44)
, (44)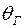 - ширина ХН антенны на уровне минус 3 дБ.
- ширина ХН антенны на уровне минус 3 дБ. . (45)
. (45) в выражении (45) следует исключить.
в выражении (45) следует исключить.


