
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель эхосигнала от камня, лежащего на днеСодержание книги
Поиск на нашем сайте
Реальные камни могут иметь самую разнообразную форму, но для упрощения решения геометрической задачи пересечения акустического луча с камнем удобнее всего представить его в виде полусферы с основанием лежащем на донной поверхности. С акустической точки зрения поверхность камня можно считать частью донной поверхности с параметрами аналогичными параметрам скалистой донной поверхности. В этом случае для расчета квадрата эффективного значения акустического давления эхосигнала от поверхности камня можно воспользоваться выражением (12), учитывая при этом постепенное увеличение угла Если считать, что фронт ультразвукового импульса плоский, то можно показать, что при равномерной дискретизации эхосигнала по дистанции площади элементарных рассеиващих площадок сферической поверхности, заключенных между соседними секущими плоскостями, равны друг другу. Для полусферы это равенство соблюдается до момента достижения фронтом ультразвукового импульса основания полусферы. На рисунке 3 в упрощенном виде представлен процесс прохождения фронта ультразвукового импульса через полусферу.
Рисунок 3 При этом предполагается, что момент соприкосновения фронта с ближней к антенне точкой полусферы точно совпадает с моментом очередной выборки амплитуды эхосигнала. К моменту следующей выборки фронт ультразвукового импульса смещается на величину
Можно предложить различные способы расчета коэффициентов
Считая для последнего полного шарового пояса значение
При расчете в соответствии с выражением (12) квадрата акустического давления от рассеивающего шарового пояса нет необходимости рассчитывать непосредственно значение угла
где Очевидно, что для начального шарового сегмента (например, на рисунке 3 с площадью Член
Если протяженность импульсного объема
Для каждого
П р и м е ч а н и е. При расчете результирующего сигнала на выходе антенны в соответствии с выражением (6) член
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.91.15 (0.009 с.) |

 по мере продвижения фронта ультразвукового импульса к центральному сечению полусферы.
по мере продвижения фронта ультразвукового импульса к центральному сечению полусферы.
 , отсекая от сферической поверхности сегмент высотой
, отсекая от сферической поверхности сегмент высотой  равна
равна  . При последующих перемещениях фронта ультразвукового импульса последовательно отсекаются шаровые пояса, площади которых
. При последующих перемещениях фронта ультразвукового импульса последовательно отсекаются шаровые пояса, площади которых  и
и 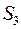 также равны
также равны  и последующие за ней должны рассчитываться в соответствии со следующим выражением
и последующие за ней должны рассчитываться в соответствии со следующим выражением . (23)
. (23) . Учитывая тот факт, что коэффициент
. Учитывая тот факт, что коэффициент 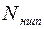 рассчитывается поправка
рассчитывается поправка 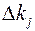 в соответствии со следующим выражением
в соответствии со следующим выражением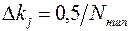 . (24)
. (24) . (25)
. (25) , (26)
, (26) - номер шарового пояса.
- номер шарового пояса. .
. , входящий в выражение (12), может быть рассчитан по следующей формуле
, входящий в выражение (12), может быть рассчитан по следующей формуле . (27)
. (27) по линии лоцирования превышает величину
по линии лоцирования превышает величину 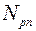 , округляя величину получаемую из следующего выражения
, округляя величину получаемую из следующего выражения . (28)
. (28) -го шарового пояса (и начального шарового сегмента, если он попадает в импульсный объем) необходимо рассчитать в соответствии с выражением (12) значение квадрата парциального акустического давления
-го шарового пояса (и начального шарового сегмента, если он попадает в импульсный объем) необходимо рассчитать в соответствии с выражением (12) значение квадрата парциального акустического давления  , создаваемого при рассеянии звука от этого пояса. После этого, для получения квадрата текущего результирующего акустического давления от поверхности камня
, создаваемого при рассеянии звука от этого пояса. После этого, для получения квадрата текущего результирующего акустического давления от поверхности камня  следует вычислить сумму квадратов акустических давлений от поясов, попадающих в импульсный объем, в соответствии со следующим выражением
следует вычислить сумму квадратов акустических давлений от поясов, попадающих в импульсный объем, в соответствии со следующим выражением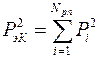 . (29)
. (29) в выражении (12) при расчете акустических давлений
в выражении (12) при расчете акустических давлений 


