
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые признаки сходимости и расходимости несобственных интегралов I рода
1. Признак сравнения. Если на промежутке [ a; +∞) непрерывные функции f (x) и g (x) удовлетворяют условию 0 ≤ f (x) ≤ g (x), то из сходимости интеграла 2. Предельный признак сравнения. Если при х 3. Если сходится интеграл
Пример 1. Вычислить несобственный интеграл По определению несобственного интеграла I рода имеем: =
Замечание. Интеграл Задание для самостоятельного решения
Найти значения несобственных интегралов или установить их расходимость:
Пример 2. Исследовать сходимость несобственного интеграла По определению несобственного интеграла I рода имеем: = || Интеграл расходится, т.к.
Задание для самостоятельного решения Исследовать сходимость несобственного интеграла:
Пример 3. Вычислить несобственный интеграл Подынтегральная функция f (x) = = 2 ∙
Задание для самостоятельного решения Найти значение несобственного интеграла или установить его расходимость: Пример 4. Исследовать на сходимость интеграл Здесь f (x) = Задание для самостоятельного решения Найти значение несобственного интеграла или установить его расходимость: Пример 5. Исследовать на сходимость интеграл Здесь f (x) =
Задание для самостоятельного решения Исследовать сходимость несобственного интеграла:
2.2. Интегралы от неограниченных функций (II рода) Если функция у = f (x) непрерывна в промежутке [ a; b) и имеет разрыв 2-го рода («убегает» в бесконечность) при x = b, то несобственный интеграл от неограниченной функции определяется следующим образом:
Если предел справа существует, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся. Аналогично, если функция у = f (x) терпит бесконечный разрыв в точке x = а, то полагают 2-го рода во внутренней точке с
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.48 (0.007 с.) |
 следует сходимость интеграла
следует сходимость интеграла 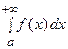 , а из расходимости интеграла
, а из расходимости интеграла  [ a; +∞), f (x) > 0, g (x) > 0 и существует конечный предел
[ a; +∞), f (x) > 0, g (x) > 0 и существует конечный предел 
 = k ≠
= k ≠  , то интегралы
, то интегралы  , то сходится и интеграл
, то сходится и интеграл  или установить его расходимость.
или установить его расходимость.
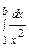 =
= =
= 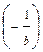 +
+ 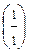 = 1. Исходный интеграл сходится и равен 1.
= 1. Исходный интеграл сходится и равен 1. сходится при p > 1 и расходится при p ≤ 1. Следовательно, его можно использовать в качестве интеграла
сходится при p > 1 и расходится при p ≤ 1. Следовательно, его можно использовать в качестве интеграла 
 .
. =
= 
 =
= || =
|| =  = 0 –
= 0 –  .
. .
.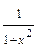 определена и непрерывна на всей числовой оси. Кроме того, она является четной. Следовательно.
определена и непрерывна на всей числовой оси. Кроме того, она является четной. Следовательно.  = 2
= 2  = 2 ∙
= 2 ∙ 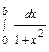 = 2 ∙
= 2 ∙  =
= = π. Исходный интеграл сходится и равен π.
= π. Исходный интеграл сходится и равен π.
 .
. > 0 при х
> 0 при х 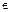 [1; +∞), при этом
[1; +∞), при этом  . Но интеграл
. Но интеграл 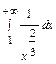 расходится (см. замечание к признакам сравнения: р =
расходится (см. замечание к признакам сравнения: р =  < 1). Следовательно, по признаку сравнения сходится и интеграл от «меньшей» функции, т.е. исходный интеграл.
< 1). Следовательно, по признаку сравнения сходится и интеграл от «меньшей» функции, т.е. исходный интеграл.
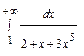 .
. > 0 при х
> 0 при х  . Вычислим
. Вычислим 
 = =
= =  =
=  ≠
≠ 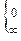 . По предельному признаку сравнения, т.к. интеграл
. По предельному признаку сравнения, т.к. интеграл  = =
= = 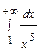 сходится (см. замечание к признакам сравнения: р = 5 > 1), то по предельному признаку сравнения сходится и исходный интеграл.
сходится (см. замечание к признакам сравнения: р = 5 > 1), то по предельному признаку сравнения сходится и исходный интеграл.


 .
. . Если функция у = f (x) терпит разрыв
. Если функция у = f (x) терпит разрыв [ a; b ], то несобственный интеграл II рода определяется формулой
[ a; b ], то несобственный интеграл II рода определяется формулой  +
+ 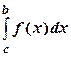 . В этом случае интеграл называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
. В этом случае интеграл называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.


