
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.1. Дифференциальное исчислениеСтр 1 из 4Следующая ⇒
Математика Методические рекомендации по подготовке к практическим занятиям и самостоятельной работе студентов.
Для студентов 2 курса очной формы обучения специальности 262019 «Конструирование, моделирование и технология швейных изделий
Печатается по решению Издательского совета колледжа
СОДЕРЖАНИЕ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Изучение дисциплины «Математика» ставит такие цели, как: ознакомление студентов с основами математического аппарата, формирование представления о роли математики, привитие умения самостоятельно изучать учебную литературу по математике и ее приложениям, развитие логического мышления. Основная часть теоретического материала изучается на лекционных занятиях, где так же разбираются типовые примеры и задачи. Некоторые темы студенты изучают самостоятельно, работая с учебниками, интернет-ресурсами. На практических занятиях студенты решают задачи и примеры по изученной теме. Целью практического занятия является не только закрепление и обобщение изученного на лекциях материала и более глубокое и детальное усвоение темы, но и раскрытие широких возможностей применения математики при изучении других дисциплин. Основными видами самостоятельной работы студентов по дисциплине «Математика» являются: изучение тем, работа с учебником, решение задач, подготовка рефератов, выполнение самостоятельных, расчётно-графических работ. Если в процессе самостоятельного изучения материала или при решении задач у студента возникают трудности, то можно обратиться к преподавателю математики для получения консультации.
Методические рекомендации по подготовке к практическим занятиям и самостоятельной работе предназначены для студентов очной формы обучения специальности 262019 «Конструирование, моделирование и технология швейных изделий». Методические рекомендации включают: тематический план учебной дисциплины, содержание дисциплины (вопросы и задания по изучаемым темам), общие рекомендации по самостоятельной работе студентов и подготовке к практическим занятиям, подготовке рефератов и по работе с литературой и интернет-ресурсами
Тематический план учебной дисциплины «математикА»
Методические рекомендации по самостоятельной работе студентов, подготовке к практическим занятиям Курс «Математики» рассчитан на 72 часа, в том числе обязательной аудиторной учебной нагрузки 48 часа (24 часа лекционных и 24 часов практических занятий); самостоятельной работы студента 24 часов. В результате освоения дисциплины студент должен уметь: - решать прикладные задачи в области профессиональной деятельности. знать: - значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы; - основные математические методы решения прикладных задач в области профессиональной деятельности; - основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики; - основы интегрального и дифференциального исчисления. Практические занятия предназначены для закрепления, обобщения и углубления знаний по изучаемой дисциплине. Основные формы проведения практического занятия это решение задач, устный или письменный опрос, беседа или диспут и т.д. Существуют общие требования и рекомендации по самостоятельной работе студентов и подготовке к практическим занятиям. Подготовка к практическому занятию начинается со знакомства с вопросами изучаемой темы. Рассмотрение этих вопросов рекомендуется начать с повторения лекционного материала. Следующим этапом подготовки является работа с учебной литературой, с монографиями и интернет-ресурсами. В методических рекомендациях предлагается список литературы. Данный список может быть дополнен студентом с учетом материалов, имеющихся в библиотеках и в Интеренете.
Настоящие методические рекомендации содержат также задания, при решении которых студенты могут проверить свой уровень подготовленности по каждой теме. На практических занятиях могут проводиться письменные контрольные работы по изучаемой теме. Ответственное и добросовестное отношение к подготовке к практическим занятиям и активное в них участие поможет студенту освоить знания и умения, предусмотренные программой курса. В ходе изучения дисциплины студентами выполняются домашние контрольные работы. При выполнении этих работ студент должен руководствоваться следующими указаниями: 1. Каждая работа должна выполняться на листах формата А4 или в отдельной тетради (в клетку). На обложке должны быть ясно написаны фамилия студента, его инициалы, номер группы, название выполняемой работы, номер варианта. 2. Решенные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условия. 3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем. 4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах. 5. Работы должны выполняться самостоятельно. Не самостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена. 6. Студент выполняет тот вариант контрольной работы, который был предложен преподавателем. В качестве самостоятельной работы студентами также выполняются рефераты. Темы рефератов выбираются из предложенного списка, который может быть дополнен и самим студентом. Объем реферата должен составлять 4-8 страниц. Требования к оформлению: шрифт – 14; интервал – 1,5; параметры страницы – 1,5 по каждому краю. Работа над рефератом должна носить творческий характер. Используя учебники, монографии, статьи и Интернет-ресурсы, студент должен весь материал переработать и кратко изложить по плану из 3-4 вопросов. Не допускается механическое включение в работу Интеренет-ресурсов, которые студентом не переработаны творчески. Интернет-ресурсы должны быть изучены с целью выборки необходимых для реферата материалов. Только после этого отредактированные элементы изученных источников включаются в реферат. В конце реферата в обязательном порядке дается список использованной литературы и Интернет-ресурсов. Рекомендации по оформлению рефератов и других творческих работ студентов можно найти в методическом пособии: УГКТиД, Н.В.Богданова, «Методические рекомендации по оформлению курсовых и дипломных проектов (работ) на ПЭВМ», 2010г. Оценка за реферат ставится с учётом таких критериев, как: · Соответствие теме и плану; · Творческий характер изложения;
· Логичность и полнота изложения материала · Грамотность изложения и оформления Данные методические рекомендации содержат задания для выполнения домашних контрольных работ и список тем для выполнения рефератов. Активная самостоятельная работа и работа на практических занятиях является условием освоения студентом дисциплины и успешной итоговой аттестации, которая осуществляется в форме дифференцированного зачёты. Дифференцированный зачёт по дисциплине «Математика» проводится по накопительной системе и в форме опроса. В процессе изучения дисциплины студенты на занятиях или самостоятельно выполняют различные задания, направленные на проверку усвоения знаний и умений. Оценивание знаний и умений студента рассредоточено во времени. Оценка на зачёте выставляется, как средний бал по результатам выполнения контрольных и домашних контрольных работ и итогового опроса. Студенты имеющие хотя бы одну оценку «2» за домашние контрольные работы к опросу не допускаются. На опросе студент должен дать развёрнутый ответ на один предложенный из списка теоретический вопрос. Во время опроса могут быть заданы дополнительные вопросы, требующие короткого ответа, а также типовые практические задания, направленные на проверку усвоения знаний и умений. Студентам, выполнившим все задания на оценки «отлично», «хорошо», «удовлетворительно», проявившим активность на занятиях, дисциплинированность, добросовестность в учёбе, выставляется дифференцированный зачёт в соответствии с накопленными текущими оценками без прохождения опроса. В методическом пособии приведены также примерные вопросы для проведения итогового опроса.
Содержание дисциплины Задания для самопроверки. Вычислить пределы: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) 38) Найти производную функции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) Вычислить значение производной в пунктах 1) -10) в точках (если она существует): x=0, x=1, x=-1, x=10, x=0.6, x=-2.5, x=9 Найти асимптоты графика функции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) Найти промежутки монотонности и экстремумы функции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) Исследовать график функции на выпуклость, вогнутость и перегибы: 1) 2) 3) 4) 5) 6) 7)
Исследовать функцию построить график: 1) 2) 3) 4) 5) 6) 7) Задания для самопроверки. Вычислить интеграл: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) 38) 39) 40) 41) Вычислить площадь фигуры, ограниченной: 1) линиями 2) эллипсом 3) линиями y = - x 2 + x + 4 и y = - x +1. 4) параболой y = x 2 + 1 и прямой x + y = 3. 5) осью Ox и синусоидой y = sin x на отрезках: а) [0, π ]; б) [0, 2 π ]. 6) параболами y 2 = 2 px и x 2 = 2 py. Вопросы. 1. Задачи, приводящие к дифференциальным уравнениям. 2. Дифференциальные уравнения первого порядка. Основные понятия. 3. Дифференциальные уравнения с разделяющимися переменными 4. Однородные дифференциальные уравнения первого порядка 5. Линейные дифференциальные уравнения первого порядка. 6. Дифференциальные уравнения высших порядков. Уравнения допускающие понижение порядка. 7. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 8. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 9. Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель. Задания для самопроверки. Решить дифференциальное уравнение: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) 38) 39) 40) 41) 42) 43) 44) 45) 46) 47) 48) 49) 50) 51) 52) 53) 54) 55) 56) 57) 58) 59) 60) 61) 62) 63) 64) 65) 66) 67) 68) 69) 70) 71) 72) 73) 74) 75) 76) 77) 78) Тема 1.4. Ряды. Вопросы. 1) Числовые ряды. Общие понятия. Сумма ряда. 2) Геометрическая прогрессия. Гармоничный ряд. Ряд Дирихле. 3) Признаки сходимости знакопостоянных рядов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.32.116 (0.265 с.) |
 и
и  . Замечательные пределы.
. Замечательные пределы.






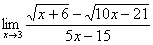

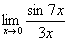






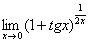





































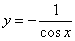























































 .
.
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. (a > 0).
(a > 0). .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
 .
.
 .
. .
. , произведя замену переменной x = 2 sin t.
, произведя замену переменной x = 2 sin t. , произведя замену переменной x = t 2.
, произведя замену переменной x = t 2.

 .
. .
.
 ,
,  .
.
 ,
,  .
. ,
,  .
. .
. .
. ,
, 













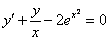 ,
,  ,
, 
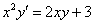 ,
, 
 ,
, 









 ,
, 
 ,
, 
 ,
,  ,
, 


 ,
, 


 ,
,  ,
, 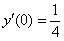 ,
, 
 ,
,  ,
, 




 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 






 ,
,  ,
,  ,
, 



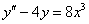
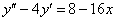



 ,
,  ,
, 
 ,
, 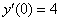



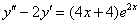
 ,
, 





