
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.2. Интегральное исчисление
Вопросы: 1. Первообразная. Неопределённый интеграл и его свойства. 2. Методы вычисления неопределённого интеграла (метод подстановки, метод интегрирования по частям) 3. Интегрирование простейших рациональных дробей. Метод неопределённых коэффициентов. 4. Определённый интеграл и его геометрический смысл. 5. Основные свойства определённого интеграла. Формула Ньютона-Лейбница. 6. Методы вычисления определённого интеграла. 7. Вычисление площадей плоских фигур. Задания для самопроверки. Вычислить интеграл: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) 38) 39) 40) 41) Вычислить площадь фигуры, ограниченной: 1) линиями 2) эллипсом 3) линиями y = - x 2 + x + 4 и y = - x +1. 4) параболой y = x 2 + 1 и прямой x + y = 3. 5) осью Ox и синусоидой y = sin x на отрезках: а) [0, π ]; б) [0, 2 π ]. 6) параболами y 2 = 2 px и x 2 = 2 py. Тема 1.3. Дифференциальные уравнения Вопросы. 1. Задачи, приводящие к дифференциальным уравнениям. 2. Дифференциальные уравнения первого порядка. Основные понятия. 3. Дифференциальные уравнения с разделяющимися переменными 4. Однородные дифференциальные уравнения первого порядка 5. Линейные дифференциальные уравнения первого порядка. 6. Дифференциальные уравнения высших порядков. Уравнения допускающие понижение порядка. 7. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 8. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 9. Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель. Задания для самопроверки. Решить дифференциальное уравнение: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) 31) 32) 33) 34) 35) 36) 37) 38) 39) 40) 41) 42) 43) 44) 45) 46) 47) 48) 49) 50) 51) 52) 53) 54) 55) 56) 57) 58) 59) 60) 61) 62) 63) 64) 65) 66) 67) 68) 69) 70) 71) 72) 73) 74) 75) 76) 77) 78) Тема 1.4. Ряды. Вопросы. 1) Числовые ряды. Общие понятия. Сумма ряда.
2) Геометрическая прогрессия. Гармоничный ряд. Ряд Дирихле. 3) Признаки сходимости знакопостоянных рядов. 4) Знакочередующиеся и знакопеременные ряды. Признаки Лейбница 5) Функциональные ряды, основные понятия. 6) Сходимость степенных рядов, интервал и радиус сходимости степенного ряда. 7) Разложение функции в ряд Тейлора и Маклорена. Задания для самопроверки. 1) Используя определение частичной суммы ряда, показать, что ряд сходится и найти его сумму 2) Показать, что ряд сходится 3) Написать пять первых членов последовательности, если ее n -й член an имеет вид: a) 4) Пользуясь необходимым признаком сходимости, показать, что ряд 5) Исследовать на сходимость ряд a) b) c) 6) С помощью признака Даламбера решить вопрос о сходимости ряда a) b) c) d) e) f) 7) Пользуясь признаком Лейбница, исследовать на сходимость знакочередующийся ряд 8) Исследовать на сходимость ряд a) b) c) d) e) 9) Исследовать сходимость ряда 10) Найти область сходимости степенного ряда 11) Исследовать на сходимость степенной ряд a) b) c) 12) Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда. 13) Разложить функцию в ряд по степеням a) b) c) d) e) f) 14) Разложить функцию 15) Разложить функцию 16) Разложить функцию Тема 2.1. Множества и отношения. Вопросы: 1. Элементы и множества. Задание множеств. 2. Операции над множествами: объединение, пересечение, разность, дополнение. 3. Законы двойственности (де Моргана). 4. Декартово произведение множеств. 5. Отображение множеств. 6. Отношения множеств (рефлексивность, симметричность, транзитивность). 7. Алгебра высказываний. 8. Определение и обозначение логических операций. 9. Основные равносильности. 10. Комбинаторика (сочетания, размещения, перестановки). Задания для самопроверки.
1) Доказать принцип двойственности: C (A U B) = CA ∩ CB, C (A ∩ B) = CA U CB. 2) Доказать равенства A U (A ∩ B) = A ∩ (A U B) = A. 3) Доказать равенства: a) CCA = A; б) 4) Доказать справедливость включения 5) Определить множества A U B, A ∩ B, A \ B, B \ A, A Δ B, если:
6) Имеем 7) Пусть A = { x: 2 ≤ x ≤ 4}, B = { y: 1 ≤ y ≤ 3}. Изобразить на плоскости xOy множество точек A × B. 8) Доказать, что (A ∩ B) × (D ∩ E) = (A × D) ∩ (B × E). 9) Начертите фигуры, изображающие множества 10) Определите свойства следующих отношений: 11) Построить таблицу истинности и определить выполнимость формулы: 12) У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? 13) Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин? 14) В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? 15) В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек? 16) Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать. 17) Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду? 18) В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире? 19) Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей? 20) Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
Примечание: в заданиях символом CA – обозначается дополнение множества A.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.131 (0.097 с.) |
 .
.
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. (a > 0).
(a > 0). .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
 .
.
 .
. .
. , произведя замену переменной x = 2 sin t.
, произведя замену переменной x = 2 sin t. , произведя замену переменной x = t 2.
, произведя замену переменной x = t 2.

 .
. .
.
 ,
,  .
.
 ,
,  .
. ,
,  .
. .
. .
. ,
, 













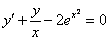 ,
,  ,
, 
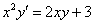 ,
, 
 ,
, 









 ,
, 
 ,
, 
 ,
,  ,
, 


 ,
, 


 ,
,  ,
, 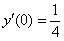 ,
, 
 ,
,  ,
, 




 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 






 ,
,  ,
,  ,
, 



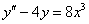
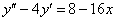



 ,
,  ,
, 
 ,
, 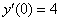



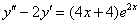
 ,
, 








 ; b)
; b)  ; c)
; c)  ; d)
; d) 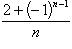 .
.
 расходится.
расходится.



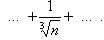














 где k - положительное число.
где k - положительное число.




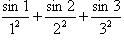




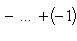





 в точках x = 1, x = 3, x = -2.
в точках x = 1, x = 3, x = -2.
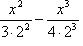



 .
.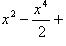
 .
.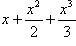


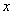 . Найти область сходимости ряда.
. Найти область сходимости ряда.
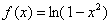




 в ряд Тейлора по степеням
в ряд Тейлора по степеням 
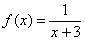 в ряд Тейлора по степеням
в ряд Тейлора по степеням  . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда. в ряд Тейлора по степеням
в ряд Тейлора по степеням  . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда. ; в)
; в)  .
.
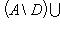
 .
.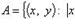



 . Показать, что
. Показать, что  .
.
 , где
, где  - вещественная плоскость. Какие фигуры изображают множества
- вещественная плоскость. Какие фигуры изображают множества  ?
?



