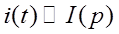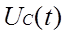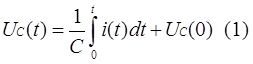Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зображення напруг на індуктивності та ємності кола при відомому зображенні струму. ⇐ ПредыдущаяСтр 5 из 5
Нехай функція
Із математики відомо, що Нехай маємо індуктивність Li(t) ----/\/\/\/\/\----->----
Нехай тепер ми маєво вітку з ємністю. Тоді:
--->-----| |-------- i(t) -->
Якщо до ()1 виконати пряме перетворення Лапласа, то
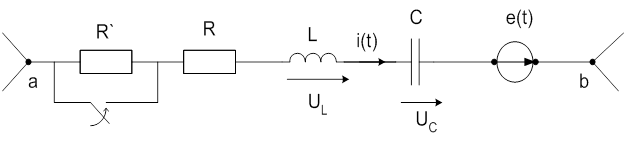
45. Закон Ома в операторной форме. Нехай маємо ділянку кола на рис.1.
Рис.1. Після замикання ключа для миттєвої напруги Uab:Uab(t)=R*i(t)+UL(t)+Uc(t)-e(t) (1) Нехай i(t)=I(p), e(t)=E(p),тоді UL(t)=L*P*I(p)-L*i(0)=UL(p); Uc(t)=Uc(p)=I(p)/(c*p)+Uc(0)/p Після застосування Лапласса до (1): Uab(p)=R*I(p)+L*p*I(p)-L*i(0)+I(p)/(c*p)+U(0)/p-E(p) (2) Для (2) можна розрахувати таку розрахункову схему:
В схемі рис. 2 крім операторних елементів для індуктивності L*p і ємності 1/C*p з‘явилися внутрішні операторні ЕРС цих елементів. Для індуктивності L*i(p),для ємності Uc(0)/p. Додатні напрямки цих операторних ЕРС пов‘язані з додатнім напрямком зображення струму. Для операторної ЕРС індуктивності L*i(0) додатній напрямок збігається з додатнім напрямом струму; для операторної ЕРС ємності додатний напрямок протилежний додатньому напрямку струму. Якщо (2) розв’зати відносно зображення струму, отримаємо: I(p)=(E(p)+L*i(0)-Uc(0)/p+Uab(p))/R+L*p-1/(C*p) (3) Вираз R+L*p-1/(C*p) (4) називають операторним опором вітки. Порівнюючи (4) з виразом Z(jw) =R+j*w*L+1/(j*w*C) (5) бачимо, що комплексний опір Z(jw) є частковим варіантом операторного опору, коли p=j*w. Якщо у вітці відсутня ЕРС і маємо нульові початкові умови i(0)=0, Uc(0)=0, то формула (3) для зображення I(p) спрощується, і має вигляд: I(p)=Uab(p)/Z(p) 46.Закони Кірхгофа в операторній формі. Перший закон Кірхгофа у використанні до вузла в колі для дійсних струмів має вигляд ∑Іk=0 Оскільки струм Іk відображається за допомогою Лапласа, а інтеграл суми дорівнює сумі інтегралів від доданків цієї суми, то перший закон Кірхгофа в операторній формі запишеться у вигляді ∑Іk(p)=0 Відповідно другий закон Кірхгофа у використанні до контуру кола ∑ ek= ∑ uk де ek – сума ЕРС джерел енергії в k -й вітці і uk – напруга на k-й вітці, записується в операторній формі: ∑ Ek(p)= ∑ Uk(p) Зрозуміло, що при складанні рівнянь Кірхгофа в операторній формі необхідно задати додатні напрямки всіх струмів і дотримуватись усі правила знаків, які задані раніше при складанні рівнянь на основі законів Кірхгофа для дійсних функцій часу. В загальному випадку для вітки, яка складає всі 3 елементи (r,L,C), маємо
t uk=rkik+Lk(dik/dt)+1/Ck∫ikdt+uck(0) згідно з ненульовими початковими умовами отримаємо Uk(p)= rkIk(p)+pLkIk(p)-Lkik(0)+Ik(p)/(pCk)+Uck(p)/p або Uk(p)+Lkik(p)-uck(0)/p=Ik(p)[rk+pLk+1/(pCk)] Величину rk+pLk+1/pCk=Zk(p) називають загальним опором вітки або операторним опором вітки. Отже при цьому операторний запис законів Кірхгофа матиме вигляд ∑Ik(p)=0; ∑Ek(p)=∑[Ik(p)Zk(p)-Lkik(p)+uck(0)/p].
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.33.178 (0.004 с.) |
 має зображення І(р).
має зображення І(р).


 -->
-->