
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 1. Расчет ставок простых и сложных процентовСтр 1 из 6Следующая ⇒
1. Содержание работы. ü Наращение простых и сложных процентов. ü Дисконтирование по простым и сложным процентам. ü Номинальная и эффективная процентные ставки. ü Эквивалентность во времени денежных сумм. 2. Теоретический материал. 2.1. Наращение простых и сложных процентов. Годовую ставку процента обозначим через i, первоначальную сумму средств Р, S – будущая наращенная сумма, n - период, срок (в годах). При простых процентах к концу n -ого года наращенная сумма станет равной: При наращении сложных процентов к концу n -ого года наращенная сумма станет равной: Обе формулы наращения процентов могут применяться и для нецелых периодов. Пусть вклад лежал n лет и еще период Δn - срок меньше года. Тогда: Если сложные проценты начисляют m раз в году при номинальной годовой процентной ставке равной i, тогда наращенная сумма за n лет равна:
Мультиплицирующий множитель или множитель наращения по сложным процентам показывает, во сколько раз возрастает за n лет сумма, положенная в банк под i процентов годовых. Для облегчения расчетов, особенно со сложными процентами, составлены таблицы мультиплицирующих множителей: При начислении процентов m раз в год вводится также годовой множитель наращения: 2.2. Дисконтирование по простой и сложной ставке процента. Дисконтирование – процесс обратный во времени процессу наращения. Дисконтирование можно производить как по простым процентам, так и по сложным процентам. Чтобы через n лет иметь на счету сумму S, надо положить сейчас на счет Для облегчения расчетов при дисконтировании по сложным процентам используются дисконтирующие множители: При начислении процентов m раз в год вводится годовой дисконтный множитель: 2.3. Номинальная и эффективная процентные ставки.
Пусть годовая процентная ставка равна i. При сложных схемах начисления процентов применяют номинальную и эффективную процентные ставки. В общем случае номинальной называется годовая процентная ставка, используемая для расчетов при начислении сложных процентов несколько раз в году, а действительная годовая ставка, которая получается при выбранной схеме начисления процентов, называется эффективной. Если начислять сложные проценты m раз в год по ставке i/m, то эффективная годовая процентная ставка равна: 2.4. Эквивалентность во времени денежных сумм. Денежные суммы S(T) в момент Т и s(t) в момент t называются эквивалентными по ставке сравнения i, если 3. Порядок работы. 3.1. Описание работы на листе Excel. Рекомендуется скопировать приведенную таблицу на лист Excel, вставить формулы в выделенные цветом ячейки, убедившись при этом, что получены те же значения. Используя построенный лист, решить задачи, приведенные в лабораторной работе, для чего следует скопировать необходимые строки на новое место на листе. Будем выбирать формат “процентный” для процентных ставок и формат “денежный” для денежных сумм (2 знака после запятой). Для поля n – (количество лет) выбираем формат “числовой с 2 знаками после запятой”, так как период может быть не целым числом лет. Для поля m(p) – формат целый. Для решения четырех задач следует ввести формулы для простых и сложных процентов. В каждой строке есть выделенное поле, которое и должно быть вычислено по значениям в остальных полях. Вначале создаем таблицу для расчетов с простыми процентами. Для расчета используется формула простых процентов: 1) Задано: начальный платеж Р, ставка процента i и срок n. Находится конечная сумма вклада
2) Задано: требуемая конечная сумма S, ставка процента i и срок n. Находится начальный платеж 3) Задано: начальный платеж Р, срок n, требуемая сумма S. Находится желательная ставка процента 4) Задано: начальный платеж Р, ставка процента i и требуемая сумма S. Находится требуемый срок хранения вклада Далее переходим к расчету сложных процентов, которые могут начисляться несколько раз в год. 1) Задано: начальный платеж Р, ставка процента i и срок n. Находится конечная сумма вклада S и эффективная процентная ставка iэф: 2) Задано: требуемая конечная сумма S, ставка процента i и срок n. Находится начальный платеж Р и эффективная процентная ставка iэф: Р = -ПС(i/m; n*m; 0; S); iэф =ЭФФЕКТ(i; m). 3) Задано: начальный платеж Р, срок n, требуемая сумма S. Находится желательная ставка процента i и эффективная процентная ставка iэф: i = СТАВКА(n*m; 0; P; -S)*m; iэф =ЭФФЕКТ(i; m). 4) Задано: начальный платеж Р, ставка процента i и требуемая сумма S. Находится требуемый срок хранения вклада n и эффективная процентная ставка iэф: n = ОКРВВЕРХ(КПЕР(i/m; 0; -P; S);1)/m; iэф =ЭФФЕКТ(i; m). В случае нескольких начислений в год, следует аккуратно вводить процентную ставку и количество периодов, не забывая, что i – годовая процентная ставка. Если производится m начислений в год, то ставка за период равна i/m, а количество периодов n*m. Подробнее специальные функции Excel описаны ниже. Следует отметить, что указанные функции могут выполнять более широкий спектр задач, поэтому для нашей цели некоторые параметры взяты нулями, некоторые опущены. При использовании функции ПЗ следует взять результат со знаком минус. 3.2. Лист Excel.
3.3. Используемые финансовые функции. ü S = БС(i/m; n*m; 0; -P) Возвращает будущее значение вклада S на основе сложных процентов с годовой процентной ставкой i, если вклад Р лежит n лет, а проценты начисляются m раз в год. Здесь Р – количество вложенных в банк средств, оно вводится со знаком минус. ü Р = -ПС(i/m; n*m; 0; S) Возвращает начальный объем вклада Р. S - это общая сумма, которую вы будете иметь через n лет, если проценты начисляются m раз в году, i - это годовая процентная ставка. ü i = СТАВКА(n*m; 0; -P; S)*m Возвращает годовую процентную ставку, под которую следует положить начальную сумму Р, чтобы через n лет получить общую сумму вклада S. Здесь Р – количество вложенных в банк средств, оно вводится со знаком минус.
ü n = ОКРВВЕРХ(КПЕР(i/m; 0; -P; S);1)/m Функция КПЕР возвращает количество лет, которое должен храниться вклад при годовой ставке i, чтобы при начальном вкладе Р к концу срока вклад возрос до значения S. Так как количество периодов может оказаться не целым, требуется использовать функцию округления с избытком до целых. После деления количества периодов на m – количество периодов начисления процентов в год получается искомое количество лет, которое, конечно же, может и не оказаться целым. Как и в предыдущей функции Р – количество вложенных в банк средств, оно вводится со знаком минус. ü Возвращает фактическую годовую процентную ставку, если заданы i - номинальная годовая процентная ставка и m - количество периодов, составляющих год.
4. Задачи к лабораторной работе. 1. Через сколько лет начальная сумма удвоится, если начисляются простые проценты по ставке 10 % годовых? 2. Через сколько лет начальная сумма удвоится, если начисляются сложные проценты по ставке 10 % годовых? 3. Определить сумму вклада, которую нужно положить в банк сроком на 2 месяца под 10% годовых (простые проценты), чтобы получить 1200 руб. 4. 7 марта в банк положили 10000 руб. под ставку 10 % годовых. Какую сумму снимет вкладчик 30 апреля? Считать, что начисляются сложные проценты методом 365/365. 5. Какая сумма предпочтительнее при ставке 6 % годовых: 1000 руб. сегодня или 2000 руб. через 8 лет? При какой ставке финансовые результаты эквивалентны? 6. Определить, какое помещение денег на срок 6 месяцев выгоднее: под простую ставку в 10% годовых или под сложную в 9% годовых при ежеквартальном начислении процентов. 7. Под какой годовой процент достаточно положить 1000 руб., чтобы через 3 года с ежеквартальным начислением сложных процентов получить 1300 руб.? 8. Номинальная процентная ставка 12 % годовых. Какова эффективная процентная ставка, если проценты начисляются ежеквартально?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 1414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.022 с.) |
 . Наращенные суммы представляют собой возрастающую арифметическую прогрессию, каждый год сумма увеличивается на величину
. Наращенные суммы представляют собой возрастающую арифметическую прогрессию, каждый год сумма увеличивается на величину 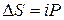
 . Предполагается, что в конце каждого года происходит капитализация процентов, т.е. их присоединение к начальной сумме. Наращенные суммы представляют геометрическую прогрессию.
. Предполагается, что в конце каждого года происходит капитализация процентов, т.е. их присоединение к начальной сумме. Наращенные суммы представляют геометрическую прогрессию. в общем случае или
в общем случае или  при смешанном начислении процентов.
при смешанном начислении процентов.
 и
и  . При начислении процентов m раз в год
. При начислении процентов m раз в год  .
. , тогда
, тогда 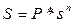 .
. (в случае простых процентов), или
(в случае простых процентов), или  (в случае сложных процентов).
(в случае сложных процентов). .
. .
.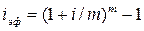 .
.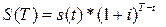 . При T > t эквивалентность сумм S(T) и s(t) означает, что сумма S(T), уменьшающаяся при движении в прошлое за каждый единичный промежуток в 1/(1+i) раз, к моменту t превратится как раз в сумму s(t). Такой пересчет называют приведением ее или нахождением ее современной величины. Сама же формула сравнения денежных сумм в любые моменты времени называется математическим дисконтированием.
. При T > t эквивалентность сумм S(T) и s(t) означает, что сумма S(T), уменьшающаяся при движении в прошлое за каждый единичный промежуток в 1/(1+i) раз, к моменту t превратится как раз в сумму s(t). Такой пересчет называют приведением ее или нахождением ее современной величины. Сама же формула сравнения денежных сумм в любые моменты времени называется математическим дисконтированием. . Из этой формулы легко получаются формулы для вычисления значений Р, n, i.
. Из этой формулы легко получаются формулы для вычисления значений Р, n, i. .
. .
. .
. ЭФФЕКТ(i; m)
ЭФФЕКТ(i; m)


