
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 3. Виды денежных потоков, ренты
1. Содержание работы. ü Потоки платежей. ü Конечная годовая рента. ü Рента конечная общая. ü “Вечная” годовая рента. ü Объединение и замена рент. 2. Теоретический материал. 2.1. Потоки платежей. Поток платежей – это последовательность величин самих платежей (со знаками) и моментов времени их осуществления. Положительные платежи это поступление, отрицательные – выплаты. Поток платежей с постоянными промежутками между ними называется рентой. Величиной потока в момент Т называется сумма платежей потока, приведенная (дисконтированная) к этому моменту. 2.2. Конечная годовая рента. Это самая простая рента, один платеж R в год, длительность ее n лет, процентная ставка i. На рентные платежи начисляются сложные проценты. Если платежи поступают в конце очередного промежутка, то рента называется постнумерандо, в начале – пренумерандо. Современная величина ренты постнумерандо Ap и пренумерандо Aa равна:
Зная современную величину ренты, можно найти ее конечную величину, которая еще называется аккумулированной суммой потока платежей Формулы для аккумулированной суммы потока платежей постнумерандо Sp и пренумерандо Sa:
2.3. Рента конечная общая. Пусть платежи производятся р раз в год через равные интервалы, R – суммарный годовой платеж, проценты начисляются m раз в год также через равные интервалы времени. Дадим формулы для аккумулированной суммы потока платежей постнумерандо Sp и пренумерандо Sa:
Зная конечную величину ренты, можно найти ее современную величину 2.4. “Вечная” годовая рента. Под “вечной”, или бессрочной, годовой рентой понимается рента, последовательность платежей которой неограниченна, т.е. продолжается бесконечно долго. Наращенная величина такой ренты бесконечна, а современная величина равна: 2.5. Объединение и замена рент. Общее правило объединения рент очень просто: находится современная величина рент-слагаемых и складывается, а затем подбирается рента-сумма с такой же современной величиной и заданными остальными параметрами. 3. Порядок работы. 3.1. Описание работы на листе Excel. Рекомендуется скопировать приведенную таблицу на лист Excel, вставить формулы в выделенные цветом ячейки, убедившись при этом, что получены те же значения. Используя построенный лист, решить задачи, приведенные в лабораторной работе, для чего следует скопировать необходимые строки на новое место на листе.
Будем выбирать формат “процентный” для процентных ставок и формат “денежный” для денежных сумм (2 знака после запятой). Для поля n – (количество лет) выбираем формат “числовой с 2 знаками после запятой”, так как период может быть не целым числом лет. Для поля m(p) – формат целый. Вначале следует ввести явные формулы для конечной общей ренты и формулы для вечной ренты. 1) Задано: годовой платеж ренты R, годовая ставка процента i, срок n, m - число начислений процентов в год и p - число выплат ренты в год. Находятся: современная А и наращенная величины ренты S постнумерандо и пренумерандо.
2) Задано: годовой платеж ренты R, годовая ставка процента i. Находится современная величина вечной ренты Далее необходимо, используя специальные финансовые функции Excel, ввести формулы для решения семи задач для конечной ренты. Следует отметить, что специальные функции Excel могут выполнять более широкий спектр задач, поэтому для нашей цели некоторые параметры взяты нулями, некоторые опущены. При использовании функции ПЗ следует взять результат со знаком минус. Некоторые финансовые функции имеют параметр “тип”. Если параметр тип = 0 или вообще отсутствует, то используются оценки постнумерандо (платежи производятся в конце периода), если параметр тип = 1 – оценки пренумерандо (платежи производятся в начале периода). Параметры “тип” и “0”, стоящие в конце списка параметров вообще могут быть опущены. 1) Задано: суммарный годовой платеж R, ставка процента i и срок ренты n. Находятся современная А и наращенная S величины ренты. А = ПС(i/m; n*m; -R/m; 0; тип), S = БС(i/m; n*m; -R/m; 0; тип). 2) Задано: наращенная величина ренты S, ставка процента i и срок ренты n. Находятся суммарный годовой платеж R и современная величина ренты А. R = -ПЛТ(i/m; n*m; 0; S; тип)*m, А = -ПС(i/m; n*m; 0; S; тип). 3) Задано: современная величина ренты А, ставка процента i и срок ренты n. Находятся суммарный годовой платеж R и наращенная величина ренты S. R = -ПЛТ(i/m; n*m; A; 0; тип)*m, S = БС(i/m; n*m; 0; А; тип).
4) Задано: суммарный годовой платеж R, наращенная величина ренты S и срок ренты n. Находятся желательная ставка процента i и современная величина ренты А. i = СТАВКА(n*m; -R/m; 0; S; тип)*m, А = ПС(i/m; n*m; -R/m; 0; тип). 5) Задано: суммарный годовой платеж R, современная величина ренты А и срок ренты n. Находятся желательная ставка процента i и наращенная величина ренты S. i = СТАВКА(n*m; -R/m; А; 0; тип)*m, S = БС(i/m; n*m; 0; А; тип). 6) Задано: суммарный годовой платеж R, наращенная величина ренты S, ставка процента i. Находятся срок выплаты ренты n и современная величина ренты А. n = ОКРВВЕРХ(КПЕР(i/m; -R/m; 0; S; тип);1)/m, А = ПС(i/m; n*m; -R/m; 0; тип) 7) Задано: суммарный годовой платеж R, современная величина ренты А, ставка процента i. Находятся срок выплаты ренты n и наращенная величина ренты S. n = ОКРВВЕРХ(КПЕР(i/m; -R/m; А; 0; тип);1)/m, S = -БС(i/m; n*m; -R/m; 0; тип). 3.2. Лист Excel.
3.3. Используемые финансовые функции. ü S = БС(i/m; n*m; -R/m; 0; тип) или S = БС(i/m; n*m; -R/m) Возвращает наращенную величину ренты S на основе годовой процентной ставки i, если платежи продолжаются m раз в год в течение n лет при годовом платеже R. ü S = БС(i/m; n*m; 0; А; тип) Возвращает наращенную величину ренты S на основе годовой процентной ставки i, если платежи продолжаются m раз в год в течение n лет. Задана также современная величина ренты А. ü А = ПС(i/m; n*m; -R/m; 0; тип) или А = ПС(i/m; n*m; -R/m) Возвращает современную величину ренты А. R – величина платежа за период, если платежи осуществляются m раз в год в течение n лет, i - это процентная ставка за год. ü А = ПС(i/m; n*m; 0; -S; тип) Возвращает современную величину ренты А. S – наращенная величина ренты, R – величина платежа за период, если платежи осуществляются m раз в год в течение n лет, i - это процентная ставка за год. ü R = -ПЛТ(i/m; n*m; 0; S; тип)*m Возвращает величину годового платежа R ренты, у которой наращенная величина S если платежи осуществляются m раз в год в течение n лет, i - это процентная ставка за год. ü R = -ПЛТ(i/m; n*m; A;0;тип)*m или R= -ПЛТ(i/m; n*m; A) Возвращает величину годового платежа R ренты, у которой современная величина А если платежи осуществляются m раз в год в течение n лет, i - это процентная ставка за год. ü i = СТАВКА(n*m; -R/m; А; 0; тип)*m или i = СТАВКА(n*m; -R/m; А)*m Возвращает i годовую процентную ставку, при которой годовой платеж R обеспечивает современную величину А за n лет. Здесь R – ежегодный платеж по ренте, это значение вводится со знаком минус, m – количество платежей в год. ü i = СТАВКА(n*m; -R/m; 0; S; тип)*m Возвращает i годовую процентную ставку, при которой годовой платеж R обеспечивает наращенную величину S за n лет. Здесь R – ежегодный платеж по ренте, это значение вводится со знаком минус, m – количество платежей в год.
ü n = ОКРВВЕРХ(КПЕР(i/m; -R/m; А; 0; тип);1)/m или n = ОКРВВЕРХ(КПЕР(i/m; -R/m; А);1)/m Функция КПЕР возвращает количество периодов, в которые выплачивается рента m раз в год при годовой ставке i, чтобы при годовом платеже R к концу срока обеспечить наращенную величину S. Так как количество периодов может оказаться не целым, требуется использовать функцию округления до целых. После деления полученного количества периодов на m – количество периодов в год получается искомое количество лет, которое, конечно же, может и не оказаться целым. Как и ранее R – годовой платеж вводится со знаком минус. 4. Задачи к лабораторной работе. 1. Поясните движение денежных сумм при 5-летней ренте с годовым платежом 1000 руб. при процентной ставке 10% годовых. 2. Найти современную и наращенную величины годовых рент (постнумерандо и пренумерандо) сроком на 10 лет при годовом платеже 200 руб., процентной ставке 7 % годовых с ежеквартальным начислением процентов. Объяснить полученные цифры. 3. Найти современную и наращенную величины ренты при годовом платеже 300 руб. (с выплатами, производимыми в конце каждого месяца), процентной ставке 6 % годовых с ежемесячным начислением процентов. Объяснить полученные цифры для сроков ренты 5 лет и 6 лет. 4. Семья хочет накопить на машину 12000 $, вкладывая в банк ежегодно по 1000 $. Годовая ставка процента в банке 7%. Как долго ей придется копить? 5. Бизнесмен арендовал виллу за 10000$ в год. Какова выкупная цена аренды при годовой ставке процента 5 %? 6. Покупатель предложил два варианта расчетов при покупке дачи: 1) 5000$ немедленно и по 1000 $ ежегодно в течение 5 лет; 2)8000 $ немедленно и по 300 $ в течение пяти лет. Какой вариант выгоднее при годовой ставке процента 5 %; 10 %? 7. В ходе судебного заседания выяснилось, что гражданин А. недоплачивал налогов 100 руб. ежемесячно. Налоговая инспекция хочет взыскать недоплаченные за последние два года налоги вместе с процентами (2 % ежемесячно). Какую сумму должен заплатить гражданин А? 8. Замените годовую ренту с годовым платежом 600 $ и длительностью 10 лет семилетней годовой рентой. Ставка процента 8 % в год.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.022 с.) |
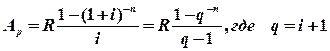 ,
,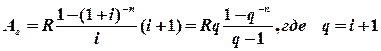 .
. .
.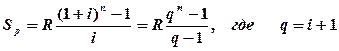

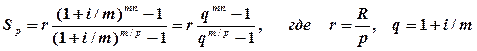

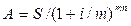 .
.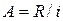 .
. ,
,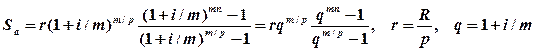 ,
,


