
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения удельных теплоемкостей по измерению скорости звука
Цель работы Целью работы является ознакомление с процессом распространения звука в воздухе и с методикой определения соотношения
Теоретические пояснения Наиболее точным и удобным методом определения отношения удельной теплоемкости В механике выводится формула, связывающая скорость распределения звука в газе
где производная должна, согласно Лапласу, вычисляться из уравнения адиабаты, которое запишем в виде: Pρ-γ = const (2) где
или для скорости звука:
Использование уравнения (2) соответствует тому факту, что распределение звука в воздухе - адиабатический процесс. Поток тепла из области сгущения в область разряжения пренебрежимо мал, если только длина волны велика по сравнению с длиной свободного пробега. Заменим отношение P/ρ в уравнении (4) его выражением, получаемым из уравнения состояния идеального газа PV = (m/μ) RT. Тогда
где μ – молекулярный вес газа, R - универсальная газовая постоянная, T- абсолютная температура. Итак, для γ получаем следующую формулу:
Таким образом, для определения показателя адиабаты достаточно знать температуру газа и измерить скорость распределения в нем звука.
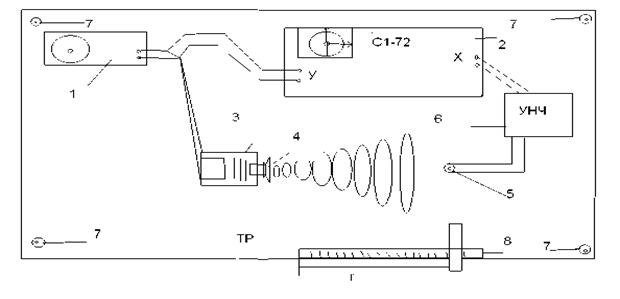
3.Установка и методика определения скорости звука в воздухе Для определения скорости звука в воздухе в данной работе используется метод сдвига фаз. Схема установки, реализующей этот метод, показана на рис.1.
Рис.1. Установка для определения скорости звука в воздухе: 1 - звуковой генератор; 2 - осциллограф; 3 - трансформатор; 4 - динамик; 5 - микрофон; 6 - усилитель низкой частоты; 7 - система блоков для перемещения микрофона; 8 - линейка, по которой перемещается микрофон.
Синусоидальные электрические колебания от звукового генератора поступают на осциллограф по двум каналам: на вход Y непосредственно по проводам, т.е. практически мгновенно, а на вход X – через систему “динамик микрофон”, которая вызывает некоторую задержку сигнала вследствие того, что участок r он проходит не со световой скоростью с, а лишь со звуковой
Δt = r/ Для синусоидальной волны
где λ – длина волны, Δφ = ωΔt = 2π r/λ (8) Разность фаз колебаний определяется на экране осциллографа по фигурам Лиссажу, которые представляют замкнутые кривые, описываемые на плоскости точкой (в данном случае – электронным лучом), участвующей одновременно в двух взаимно перпендикулярных колебательных движениях. Поскольку на выходы X и Y поступают колебания одинаковой частоты, но с фазами, сдвинутыми на Δφ, то можно записать:
где
При Δφ = 0 эллипс вырождается в прямую, описываемую уравнением:
а при
Фигуры Лиссажу (10), (11), (12) показаны на рис. 2. Фигуры (11) и (12) наиболее удобны для визуального определения разности фаз колебаний. Из (8) и (9) видно, что прямая (11) будет появляется на экране при
Х Х Х
а б в Рис. 2. Фигуры Лиссажу: а) для
Следовательно, расстояние Δr между соседними картинками рис. 2б и рис. 2в будет:
Формулы (7) и (13) дают скорость звуковой волны в воздухе:
где ν - частота звукового генератора. Соотношение (14) позволяет избежать измерения весьма неопределённого расстояния между динамиком и микрофоном как рассредоточенными передающей и приёмной системами. Установка собрана в деревянном ящике. Для уменьшения влияния отражения звука от различных поверхностей внутренняя поверхность ящика оклеена звукопоглощающим материалом. Передвижение микрофона относительно динамика осуществляется ниткой, пропущенной через систему блоков. На поверхности верхней грани ящика имеется шкала, по которой можно измерить (по стрелке шкалы) величины перемещений микрофона.
Примечание. Усилитель низкой чистоты служит для усиления сигнала микрофона до уровня чувствительности осциллографа. Трансформатор – для согласования выхода звукового генератора с низкой нагрузкой (динамиком).
Порядок выполнения работы 1. Включить осциллограф, звуковой генератор и усилитель низкой чистоты (УНЧ). Исходные положения регулировок приборов: а) Усилитель: Регулировки тембров (высокие и низкие) выведены влево до предела. Громкость в крайнем левом положении. б) Генератор: Частота – 1200 Гц, клавиша F×10 - в утопленном положении, выходное напряжение - 2,8 В, регулировка выхода - в положении 3. в) Осциллограф: Регулировка передней панели осциллографа в следующих положениях: Переключатель «время/дел» - в положении 0,5 ms; Клавиша «вход Х» - в утопленном положении; Яркость умеренная (среднее положение); Усиление – 2 В/дел. При этом из динамика должен быть слышен достаточно громкий звук (частотой 1200 Гц), а на экране осциллографа видна одна из фигур Лиссажу. Смещением луча по вертикали и горизонтали установить ее в середине экрана. После этого никакие регулировки приборов, кроме частоты генератора, трогать не следует. 2. Сместить микрофон, установить стрелку шкалы на 10 см. Медленно отодвигая микрофон от динамика (стрелка шкалы движется влево), записать с точностью до 2 - 5 мм положение микрофона (по стрелке шкалы), при которых эллипс на экране осциллографа стягивается в прямую (11) и (12) (рис. 2, б и 2, в). Микрофон отодвигать до расстояния, при котором стрелка шкалы находится на положении ≈ 60 см. При измерениях следует избегать всяких шумов, так как они, поступая через микрофон и усилитель на осциллограф, смазывают картину. 3. Измерения повторить при частотах генератора 1400, 1600, 1800 и 2000 Гц по 3 раза. 4. Выключить все три прибора (сначала тумблеры, потом из розеток). 5.Данные записать в таблицу 1.
Таблица 1.
6. Для каждой частоты вычислить
5.Контрольные вопросы 1. Дайте общее определение теплоемкости С, теплоемкостей Чему равно отношение 2. При какой частоте 3. При каком давлении 5. Выведите соотношение, связывающее скорость звука со среднеквадратичной скоростью молекул? 6. Выведите уравнение (6). 7. Как изменится выражение для скорости звука, если при выводе вместо уравнения (2) воспользоваться предположением Ньютона о том, что распространение звука в воздухе – изотермический процесс, описываемый законом Бойля-Мариотта? Выведите формулу для этого случая и подсчитайте, насколько результаты отличаются от истинных для одно-, двух- и трехатомных молекул?
8. Выведите уравнение фигур Лиссажу для вырожденных случаев. 9. Чему равно отношение скоростей звука в гелии и водороде, находящихся при одинаковой температуре?
ЛАБОРАТОРНАЯ РАБОТА 1-5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.25 (0.019 с.) |
 по измерениям скорости звука.
по измерениям скорости звука. и относительное изменение давления с плотностью:
и относительное изменение давления с плотностью: (1)
(1) . Дифференцируя (2), получим соотношение:
. Дифференцируя (2), получим соотношение: (3)
(3) (4)
(4) (5)
(5) (6)
(6)

 (7)
(7) – частота. Тогда для разности фаз колебания на выходах X и Y получим:
– частота. Тогда для разности фаз колебания на выходах X и Y получим: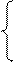
 (9)
(9) и
и  – амплитуды колебаний по осям X и Y, соответственно. Уравнение траектории луча определяется исключением из системы (9) параметра t. Легко показать, что это будет эллипс:
– амплитуды колебаний по осям X и Y, соответственно. Уравнение траектории луча определяется исключением из системы (9) параметра t. Легко показать, что это будет эллипс: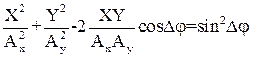 (10)
(10) (11)
(11) – в прямую
– в прямую (12)
(12) ; r = kλ, а прямая (12) - при
; r = kλ, а прямая (12) - при 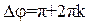 ; r= (k + 1/2)λ, где k = 0,1,2…
; r= (k + 1/2)λ, где k = 0,1,2…
 У У У
У У У


 , формула (10), б) для
, формула (10), б) для 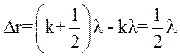 (13)
(13) (14)
(14) , Гц
, Гц
 , см
, см
 , см
, см
 , см
, см
 , а по формуле (6) – определить величину γ, приняв μ = 29 г/моль, Т = 300 К.
, а по формуле (6) – определить величину γ, приняв μ = 29 г/моль, Т = 300 К. и
и  .
. , длина собственного пробега l молекул газа, находящегося при нормальных условиях, равна длине волны λ? Выполняется ли в настоящем эксперименте необходимое условие l << λ?
, длина собственного пробега l молекул газа, находящегося при нормальных условиях, равна длине волны λ? Выполняется ли в настоящем эксперименте необходимое условие l << λ? длина свободного пробега ℓ молекул воздуха равна длине волны звука λ, используемого в эксперименте диапазона? Выполняется ли в настоящем эксперименте условие
длина свободного пробега ℓ молекул воздуха равна длине волны звука λ, используемого в эксперименте диапазона? Выполняется ли в настоящем эксперименте условие  <<
<<  , где
, где 


