Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения удельных теплоемкостей воздуха методом клемана – дезорма
1. Цель работы Целью работы является ознакомление с газовыми законами и с методикой определения отношения СР/СV методом адиабатического расширения (Клемана-Дезорма). Теоретические пояснения Процессы, которые происходят в газах, подчиняется одному из основных законов природы - закону сохранения и превращения энергии. Выражением этого закона является первое начало термодинамики. В достаточно общей форме оно может быть сформулировано так: количество теплоты δQ, сообщенное системе, расходуется на увеличение внутренней энергии системы dUи насовершение системой работы δА против внешних сил: δQ = dU + δА (1) Количеством теплоты называется энергия, передаваемая от одного тела к другому в процессе теплообмена. Внутренней энергией можно назвать кинетическую и потенциальную энергию (энергию взаимодействия) его молекул. Газ, обладающий такими же свойствами, как и совокупность невзаимодействующих материальных точек, называют идеальным газом. Многочисленные опыты показали, что реальные газы при не слишком низких температурах и достаточно малых давлениях по своим свойствам близки к идеальным газам. Так, водород и гелий уже при атмосферном давлении и комнатной температуре ведут себя практически как идеальные газы. Состояние газообразной системы определяется заданием трех термодинамических параметров Р, V и Т, связанных между собой уравнением состояния (для идеального газа – это уравнение Менделеева-Клапейрона): ƒ (P,V,T) = 0. (2) Среди процессов, которые могут происходить в газах, встречаются так называемые изопроцессы, при которых один их трех параметров состояния (Р, V или Т) сохраняется постоянным. Такими процессами являются изобарный, изохорный и изотермический. Изохорическим (изохорным) называется процесс, когда система переходит из одного состояния в другое при постоянном объеме. Изобарическим (изобарным) называется процесс, когда система переходит из одного состояния в другое при постоянном давлении. Изотермическим называется процесс, когда система переходит из одного состояния в другое при постоянной температуре. Если веществу сообщить количество тепла δQ, то его температура увеличится на dТ. Отношение бесконечно малого количества теплоты, полученного веществом, к соответствующему приращению его температуры называется теплоемкостью вещества:
C = δQ/ dТ(3) Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью: Сm= (1/m)С. Так как система может быть нагрета в результате различных процессов, необходимо еще указать условия, при которых происходит нагрв. У газа различают теплоемкость при постоянном объеме CVи теплоемкость при постоянном давлении СP. При постоянном объеме работа внешних сил δА = P dV равна нулю, и всё сообщаемое газу извне количество теплоты целиком идет на увеличение его внутренней энергии U.Отсюда теплоемкость газа при постоянном объеме СV численно равна отношению приращения внутренней энергии одного моля газа dUк приращению его температуры dT. Cv = (∂U/∂T)V (4) При нагревании газа при постоянном давлении газ расширяется, сообщаемое ему извне количество теплоты идет не только на увеличение его внутренней энергии, но и на совершение работы δАпротив внешних сил. Следовательно, теплоемкость газа при постоянном давлении больше теплоемкости при постоянном объеме на величину отношения работы (для идеального газа внутренняя энергия является функцией только температуры), которую совершает один моль газа при расширении, к приращению его температуры СP = (δQ/ dТ)P = (∂U/∂T)P + Р(∂V/∂T)P (5) Для моля идеального газа уравнение (2) имеет вид: PV = RT.Тогда в уравнении (5) (∂V/∂T)P = R/P. В результате получается уравнение Роберта Майера: СP – СV = R. Знание теплоемкостей СP, СV важно при рассмотрении адиабатических процессов. Адиабатическим называется такой процесс, при котором система переходит из одного состояния в другое без теплообмена с внешней средой (например, достаточно быстрое расширение или сжатие газа). Если в идеальном газе происходит адиабатический процесс, то PV γ = const, γ = СР/СV, (6) где показатель адиабаты γ есть отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме. Для идеального газа γ может быть рассчитана теоретически, если воспользоваться постулатом о равнораспределении энергии по степеням свободы (для системы, находящейся в тепловом равновесии при температуре Т).
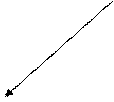
Числом степеней свободы i тела называется число независимых координат, которые необходимо задавать для того, чтобы полностью определить положение тела в пространстве. Материальная точка, произвольно движущаяся в пространстве, обладает тремя степенями свободы (X, У, Z). Молекулы одноатомного газа можно рассматривать как материальные точки на том основании, что их масса сосредоточена в ядре, размеры которого очень малы (10-13 см). Молекула одноатомного газа может иметь лишь три степени свободы поступательного движения. Молекулы, состоящие из двух, трех и более числа атомов, не могут быть уподоблены материальным точкам. Молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга. Такая молекула, помимо трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения вокруг осей X и Y (рис. 1). Вращение вокруг оси Z рассматривать не следует, т.к. предполагается, что атомы не имеют размеров.
X
Рис. 1. Модель двухатомной молекулы с двумя степенями свободы вращения вокруг осей X и Y. Молекулы, состоящие из трех и более атомов, не расположенных на одной прямой, обладают шестью степенями свободы: три от поступательного движения и три от вращения вокруг трех взаимно перпендикулярных осей. Согласно теореме о равнораспределении энергии по степеням свободы, на каждую степень свободы системы приходится одинаковая кинетическая энергия: EК = ½ kТ где k = 1,38·10-23 Дж/К – постоянная Больцмана. В идеальном газе нет сил взаимодействия между молекулами, а, следовательно, равна нулю и их взаимная потенциальная энергия. Таким образом, на одну степень свободы молекулы идеального газа приходится энергия E = ½ kТ, а на i степеней свободы Ei = (i/2) kТ. Для моля идеального газа внутренняя энергия U = (1/2) kТNА, где NА = 6,02*1023 моль -1 – число Авогадро. Тогда, учитывая, что kNА= R, где R = 8,31 Дж/K моль – универсальная газовая постоянная, получаем: U = (i/2)RT. Зная аналитическое выражение для U,получаем значение CV для идеального газа: CV = (i/2)R (7) Используя уравнение Майера CP – CV = R, получаем выражение для CP: CP = R (i+2)/2. (8) Тогда для γ: γ = CP / CV = (i+2)/i (9) Для воздуха, состоящего из смеси двухатомных газов N2 и O2, i = 5, откуда γ = 1,4.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.008 с.) |
 Z
Z

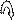 У
У