Основные характеристики имени. Виды имен.

Учебно-методическое пособие

 

ПРЕДМЕТ И ЯЗЫК ЛОГИКИ

Логика - это наука, которая исследует структуру мышления, рас­крывает лежащие в его основе закономерности.

Мышление неразрывно связано с языком. Содержание мышления только благодаря языку становится реальностью. Строение и способ употребления языка дает нам знания о формах и законах мышления.

При логическом анализе язык рассматривается как знаковая сис­тема.

Знак - это материальный объект, используемый для обозначения любого другого объекта. Логика исследует знаки-символы, состав­ляющие большинство слов естественного языка. Их связь с обозна­чаемыми предметами устанавливается либо по соглашению, либо стихийно при формировании языка.

Знаки-символы имеют предметное и смысловое значение. Пред­метным значением обладает тот объект, который представляется (или обозначается) знаком; смысловым значением - выражаемая знаком характеристика объекта. Примером смыслового значения является знак, несущий информацию об этом объекте. Предметное значение часто называют просто значением, а смысловое значение - смыслом. Например, значением знака «число, которое является про­стым и четным» выступает число 2; именно оно обозначается дан­ным словосочетанием. Смысл же этого знака - информация, кото­рую он содержит о числе 2, а именно, сложный признак числа «быть простым и четным».

Наука о знаках называется семиотикой. В этой науке выделяют три раздела - синтаксис, семантику и прагматику, что связано с су­ществованием трех аспектов языка.

Синтаксический аспект составляет многообразие отношений между знаками и включает правила образования одних знаков из других, правила изменения знаков (склонение, спряжение) и т. д.

Семантический аспект составляет совокупность отношений знаков к представляемым ими объектам, т. е. смысл и значение зна­ков.

Прагматический аспект включает отношение человека к знакам, а также отношения между людьми в процессе знакового общения.

При логическом анализе языка отвлекаются от прагматических характеристик.

Различают естественные и искусственные языки. Естественные (национальные) языки возникли как средство общения между людьми; их формирование и развитие представляет собой длитель­ный исторический процесс и происходит, в основном, стихийно. Искусственные языки сознательно создаются человеком для реше­ния определенных задач. Одним их таких языков является формали­зованный язык логики. Его характеризуют точность, краткость, строгие правила образования сложных выражений из элементарных и преобразования одних выражений в другие.

Логика исследует форму мыслей, отвлекаясь от конкретного со­держания. Логическая форма - это способ связи содержательных частей мысли. Содержательные части мысли - имена и высказыва­ния, которые фиксируются с помощью переменных А, В, С, D и т. д.

Содержательная конкретизация переменных называется значе­ниями этих переменных. Для связи переменных используются ло­гические константы, которые сохраняют свое значение в любом рассуждении. В качестве логических констант выступают слова «и», «или», «если, то», «неверно, что», «все», «некоторые» и др. Для обозначения логических констант употребляются символы, позво­ляющие более строго и компактно записать логическую форму (см. раздел «Высказывание»). Имена и высказывания являются основ­ными семантическими (логическими) категориями.

Итак, выявить логическую форму (структуру) мысли значит формализовать ее. Так, высказывания: «Все выпускники имеют выс­шее образование», «Все прямоугольники - четырехугольники», «Все металлы - проводники электричества» - имеют одинаковую схему построения: «Все S есть Р». Рассмотрим более сложные при­меры: «Если все студенты нашего курса изучают логику, а я - сту­дент нашего курса, то я изучаю логику», «Если все металлы - про­стые вещества, а литий - металл, то он - простое вещество». Эти рассуждения построены по схеме: «Если А и В, то С». Выделенные схемы являются логическими формами.

Правильная связь мыслей обусловливается законами логики, ко­торые предостерегают от ошибок в рассуждениях безотносительно к конкретному содержанию.

Логический закон ~ это логическая форма, которая порождает истинное высказывание при любой подстановке вместо переменных их значений.

Рассуждение, форма которого - логический закон, называется правильным. Правильность отличают от истинности мышления. Мысль является истинной, если она соответствует действительно­сти. Можно рассуждать правильно, но исходить из ложных данных, что приведет к ложному заключению. Так, из ложного высказыва­ния «Все сплавы - простые вещества» выводится высказывание «Некоторые простые вещества - сплавы», которое также является ложным.

Соблюдение правильности при истинных исходных данных ве­дет к истинным результатам. Это свойство мышления было замече­но в глубокой древности. Логика как отдельная наука сложилась в IV в. до нашей эры. Ее основателем является древнегреческий фи­лософ Аристотель, который сформулировал основные законы логи­ки и разработал учение о силлогистических умозаключениях.

Учение Аристотеля получило дальнейшее развитие в Средние века и в Новое время. Существенным дополнением к этому учению явилась теория индукции, разработанная английским философом Ф.Бэконом в XVI-XVII вв. и систематизированная английским логи­ком Д.С.Миллем в XIX в.

Дедуктивная логика Аристотеля и индуктивная логика Бэкона-Милля - основные направления в развитии логики вплоть до сере­дины XIX в. Логику, основанную Аристотелем, принято называть формальной, или традиционной логикой.

Во второй половине XIX в. сложилась символическая, или мате­матическая логика. Она возникла как результат применения матема­тических методов к решению логических проблем. Идея использова­ния вычислительных методов в любой науке принадлежит немецкому мыслителю Лейбницу (XVII - XVIII вв.); реально она воплотилась в работах Дж. Буля, У. Джевонса, Г. Фреге, П.С. Порецкого, Б. Рассела и др. ученых, которые создали основные разделы математической логики, ставшей важнейшей ветвью формальной логики. Математи­ческая логика нашла широкое применение в технике, где благодаря информационно-логическим машинам осуществляются сложные вы­числения, управление автоматическими приборами и т. п.

Сегодня развитие формальной логики идет в направлении разви­тия неклассических логик (логики оценок, вопросов, временной, индуктивной и др.), создания их общей теории и расширения сферы применения формальной логики.

Современная логика включает две относительно самостоятель­ные науки: логику формальную и логику диалектическую. Фор­мальная логика изучает формы мышления, выявляет структуру, общую для различных по содержанию мыслей. Диалектическая логика исследует основные закономерности процесса познания, его возникновение, изменение и развитие.

Формальная и диалектическая логика развиваются в тесном взаимодействии, которое проявляется в практике научно-теорети­ческого мышления, использующего в процессе познания как фор­мально-логический аппарат, так и средства, разработанные диалек­тической логикой.

Итак, изучение логики позволяет овладеть формами, законами и методами правильного мышления, гарантирующими грамотное преобразование высказываний, четкую формулировку определений, уверенность в аргументации и др.

 

 

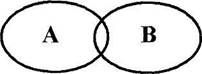
Пересечение.

Рис. 2.2: А - депутат; В - юрист

В отношении пересечения находятся два и более имен в случае, если их объемы лишь частично совпадают.

Подчинение.

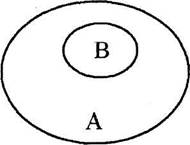
Рис. 2.3: А - юрист; В - адвокат,

Объем имени В полностью входит в объем имени А, однако не исчерпывает его.

 

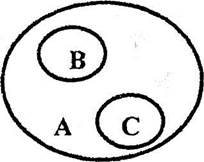
I. Соподчинение.

Рис. 2.4: А - элементарная частица; В - протон; С - фотон

В отношении соподчинения находятся имена В и С («Ни одно В не есть С»), По отношению к имени А они находятся в отношении подчинения.

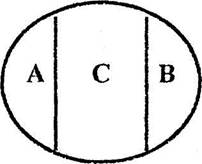
2. Противоположность .

Рис.2.5: А - храбрость; В - трусость

А и В занимают крайние места в последовательном ряду отно­шения, не исчерпывая при этом объема имени С. Имя В не только отрицает содержание имени А, но и заменяет его признаки на про­тивоположные («старый - молодой», «белый - черный»).

Противоречие

 

 

 

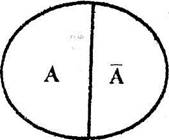
Рис. 2.6:

А - белый; не-А - не-белый

Имена А и А (не-А) находятся в отношении противоречия в том случае, если имя А отрицает признаки А, не замещая их какими-либо другими признаками. Имя А является положительным, А -соответствующим ему отрицательным именем.

Классификация имен

По объему имена делятся на единичные, общие и пустые.

Единичные - это имена, объем которых равен единице, т. е. в действительности данному имени соответствует единственно возможный предмет. Например: «Беларусь», «самое глубокое озеро в мире».

Общие - это имена, объем которых равен либо больше двух, т. е. предметы, соответствующие данным именам, не являются уникаль­ными. Таких имен - подавляющее большинство. Например: «сту­дент», «атом», «созвездие», «геометрическая фигура».

Пустые - это имена, объем которых равен нулю. Они не имеют соответствующей предметной интерпретации в действительности, но имеют определенное содержание. К этому виду относятся имена из сферы человеческой фантазии («кентавр», «леший»), а также имена, образованные с нарушениями логики («круглый квадрат»). Пустые имена могут выполнять функцию модельной репрезентации («абсолютно черное тело», «идеальный газ»). Они образуются пу­тем акцентирования одного отличительного признака предмета при полном абстрагировании от других, даже неразрывно связанных с ним, качеств и отношений. Выделение существенного признака (в данном контексте) позволяет данному типу имен выполнять эталон­ную функцию в научном познании.

По содержанию имена делятся на следующие группы:

1) конкретные и абстрактные;

2) положительные и отрицательные;

3) относительные и безотносительные;

4) собирательные и несобирательные.

Конкретным называется имя, обозначающее материальный или идеальный класс предметов («электрон», «число», «книга», «земле­трясение»).

Абстрактным называется имя, обозначающее отдельные призна­ки, качества или свойства предмета мысли, взятые отдельно от само­го предмета («симметрия»; «неравенство», «жесткость», «белизна»).

Положительным называется имя, фиксирующее наличие у предмета мысли определенного качества или отношения («аккурат­ность», «грамотность»).

Отрицательным называется имя, фиксирующее отсутствие у предмета мысли определенного качества или отношения. В русском языке, как правило, данные имена формируются с помощью отрица­тельной частицы «не» (неаккуратный, несимметричный). Если имя без частицы «не» не употребляется, оно является положительным (беспечность, ненастье).

Относительным называется имя, отражающее такой предмет мысли, который всегда предполагает наличие другого, парного ему имени (день - ночь, плюс - минус, числитель — знаменатель).

Безотносительным называется имя в том случае, если обозна­чаемый им предмет не предполагает другого соотносимого с ним предмета (чертеж, дом).

Собирательным называется имя, в котором группа однородных предметов мыслится как единое целое (стая, коллектив, ансамбль).

Несобирательным называется имя, которое предполагает воз­можность его применения относительно каждого элемента класса (цветок, здание).

 

Сложное высказывание

Логическое значение сложного высказывания в современной ло­гике ставится в зависимость (является функцией) от логических значений простых высказываний. Последние рассматриваются в качестве исходных элементов логики высказываний, ее строитель­ных блоков.

Сложные высказывания образуются из простых с помощью ло­гических союзов (операций). Важнейшие из них - отрицание, конъ­юнкция, дизъюнкция (слабая и сильная), импликация, эквива-ленция. Принято называть сложное высказывание именем логиче­ского союза, с помощью которого оно образовано.

Отрицанием высказывания Р называется высказывание, обозна­чаемое выражением Р, которое истинно тогда и только тогда, когда Р ложно. Данное определение можно выразить с помощью табл. 3.2 (таблицы истинности), где «И» обозначает «истинно», а «Л» -

«ложно».

Таблица 3.2

 

р	Не-р
и л	л и

Конъюнкцией высказываний Р и Q называется высказывание, обозначаемое выражением Р л Q, которое истинно тогда и только тогда, когда Р и Q истинны (см. 3-й столбец табл. 3.3). Выражение Р л Q читается «Р и Q».

Таблица 3.3

 

р	Q	PÙQ	PvQ	P v Q	P→Q	P↔Q
и л и л	и и л л	и л л л	И И И Л	Л и и л	И И Л И	И Л Л И

Дизъюнкцией слабой высказываний Р и Q называется высказы­вание, обозначаемое выражением PvQ, которое истинно, когда хо­тя бы одно из выражений Р и Q истинно (см. 4-й столбец табл. 3.3). Выражение PvQ читается «Р или Q».

Дизъюнкцией сильной высказываний Р и Q называется высказы­вание, обозначаемое выражением P v Q, которое истинно тогда и только тогда, когда только одно из выражений Р и Q истинно (см. 5-й столбец табл. 3.3). Выражение P v Q читается: «Либо Р, либо Q».

Импликацией высказываний Р и Q называется высказывание, обозначаемое выражением Р -» Q, которое ложно тогда и только тогда, когда Р истинно, a Q ложно (см. 6-й столбец табл. 3.3). Выра­жение читается: «Если Р, то Q», «Из Р следует Q» и т. д. При этом Р называется основанием, a Q - следствием импликации.

Эквиваленцией высказываний Р и Q называется высказывание, обозначаемое выражением Р ↔Q, которое истинно тогда и только тогда, когда логические значения Р и Q совпадают (см. 7-й столбец табл. 3.3). Выражение P↔Q читается: «Р тогда и только тогда, ко­гда Q», «Р эквивалентно Q».

Названные операции могут применяться для действий как с про­стыми, так и со сложными высказываниями.

Зная логические значения исходных высказываний, можно со­ставить таблицу истинности высказываний более сложной формы. Порядок выполнения операций при этом указывается скобками.

Упражнения

1. Установить, какие из следующих предложений являются, а ка­кие не являются высказываниями:

1). Всякая общественно-экономическая формация имеет своей основой способ производства материальных благ. 2). Был ли Наполеон французским императором? 3). Наполеон никогда не был французским императором. 4). Водители, не нарушайте правила дорожного движения! 5). Цена товара X меньше его стоимости.

2. Установить вид высказываний по характеру предиката:

1). Все кошки - млекопитающие.

2). Некоторые множества бесконечны.

3). Спрос рождает предложение.

4). Верста больше километра.

5). Сравнение - это мысленная операция.

6). Каждый человек моложе своих родителей.

7). Этот человек не имеет чувства юмора.

8) Солнце - звезда.

9). Атлантида не существует.

10). Существует любовь.

11). Минск древнее Могилева.

12). Иван уважает Алексея.

 

3. Установить количество и качество следующих высказываний:

1). Наукообразное преподнесение лжи гипнотически действует на доверчивого человека.

2). В любой библиотеке есть книги, к которым обращаются очень редко.

3). Многие выдающиеся математики не приняли неевклидовой геометрии.

 

4. Привести следующие высказывания к одной из четырех форм
и выразить в символическом виде:

1). Некоторые проблемы человеческой истории до сих пор не решены.

2). Каждый кулик свое болото хвалит.

3). Ни один ученый не мыслит формулами (А. Эйнштейн).

5. Установить распределенность терминов в следующих выска­зываниях:

1). В первобытном обществе не существовало никакой власти, которая была бы обособлена от общества и как бы стояла над ним.

2). Должностные лица наделены особыми полномочиями совер­шать от имени государства те или иные властные действия.

3). Никакая поддержка террористических банд не может быть оправдана.

4). Некоторая часть преобразующей деятельности человека нега­тивно изменяет условия развития естественных систем.

5). 70 % всего мирового грузооборота перевозится морским пу­тем.

6). Только талантливый оратор не говорит заученными фразами.

7). Ни один человек не должен страдать за правду.

8). Ни один человек не живет два века.

9). Незаконная сделка является недействительной.

10). Юность планеты хочет видеть мир свободным от насилия и войн.

11). Маршал Жуков - выдающийся полководец второй мировой войны.

12). Деньги есть условный эквивалент товара.

6. Образовать высказывания всех форм (А, Е, J, О) из следующих пар:

1). Русский князь (S); сторонник централизованной власти (Р).

2). Моральная норма (S); правовая норма (Р).

3). Русский феодал (S); сторонник преобразований Петра I (P). 4). Иван (S); брат Марьи (Р).

7. Выяснить, в значении каких логических союзов употребляют­ся грамматические союзы в следующих предложениях. Записать в символической форме.

1). Хоть редко, да метко.

2). «Почтенный старец этот постоянно был сердит или выпивши, или выпивши и сердит вместе» (А.И. Герцен).

3). «Храбрец или сидит в седле, или тихо спит в сырой земле» (Р. Гамзатов).

4). Движение яхты было возможно лишь тогда, когда дул ветер.

5). «Стоило отцу заикнуться о плате, как капитан с яростью при­нимался сопеть» (Р. Стивенсон).

6). Атеросклероз чаще всего поражает жителей больших городов и людей умственного труда.

8. Записать следующие сложные высказывания в символической форме:

1). Фемистокл знал каждого жителя Афин в лицо и по имени.

2). Каждый из нас знает книгу или хотя бы имя Альфреда Брема.

3). Неверно, что он готовился к уроку и решит эту задачу. - 4). Неверно, что он готовился к уроку, однако он решит эту задачу.

5). Неверно, что ветер дует, если и только если нет дождя.

6). Тело сохраняет состояние покоя или равномерного прямоли­нейного движения, если только оно не вынуждено изменить это со­стояние под влиянием действующих сил.

9. Дано истинное высказывание Р. Можно ли установить логиче­ское значение Q в высказывании (Q v Р) -> Р?

10. Пользуясь значениями логических союзов, решить следую­щую задачу.

В деле об убийствах имеются двое подозреваемых - Петр и Павел. Допросили четырех свидетелей, которые последовательно дали такие показания: «Петр не виноват», «Павел не виноват», «Из двух первых показаний по меньшей мере одно истинно», «Показания третьего ложны». Четвертый свидетель оказался прав. Кто преступник?

 

11. Построить таблицу истинности высказывания (Р ↔ Q) →Q.

12. Проверить, являются ли следующие высказывания истинными:

1). ((A → B)v C) ↔ ((Ā Ù В) → С).

2). (А v В) → (А ↔ С) Ù С.

3). (А Ù В) → (В v С) Ù (А ↔ С).

4). ((А → С) v В) Ù А) → (А Ù В).

13. Перевести на язык логики высказываний следующие выра­жения:

1). «Он молчит, а Варенька поет ему «Виют витры» или глядит на него задумчиво своими темными глазами, или вдруг зальется: «Ха-ха-ха!»» (А.П. Чехов).

2). «Если кто из товарищей опаздывал на молебен, или до него доходили слухи о какой-либо проказе гимназистов, или видели классную даму поздно вечером с офицером, то он очень волновался и все говорил, как бы чего не вышло» (А.П. Чехов).

3). «Если я долго не приезжал в город, то, значит, я был болен или что-нибудь случилось со мной, и они оба сильно беспокоились» (А.П. Чехов).

14. Построить таблицы истинности для следующих логических форм:

1). ((не-В→ A)vB) ↔A.

2). ((A vB)vC) → (B→ С)..

3). C→ ((BvD) Ùне-C).

15. Являются ли равнозначными следующие высказывания (по­парно):

1). Иван и Марья друг друга не любят; неверно, что Иван любит Марью, а Марья любит Ивана.

2). Каждый студент нашего курса способен или трудолюбив; не­верно, что каждый студент нашего курса не способен и не трудолю­бив.

3). Число четное тогда и только тогда, когда оно делится на 2; ес­ли число четное, то оно делится на 2, а если число нечетное, то оно не делится на 2.

4. ЗАКОНЫ ЛОГИКИ

Законы формальной логики связаны с истинностью (правильно­стью) мышления. В них выражается определенность, последова­тельность, непротиворечивость и обоснованность мыслительного процесса. Законы логики являются принципами правильного рассу­ждения в ходе доказательства истинности или опровержения лож­ности высказываний.

Специфика законов логики в том, что в качестве значений пере­менных, входящих в структуру логических форм, выступают от­дельные высказывания как целостные образования. Какие бы вы­сказывания ни подставлялись вместо переменных в логический за­кон, результат будет одним и тем же: полученное сложное высказы­вание будет истинным.

Наиболее простыми законами логики высказываний являются за­коны с одной переменной - закон исключенного третьего, закон не­противоречия, закон тождества, законы удаления и введения двой­ного отрицания.

Закон исключенного третьего - это форма AvA. Если в эту форму вместо А подставить какое-либо высказывание, то в результате всегда получается сложное истинное высказывание. Данный закон гласит: из двух противоречащих высказываний одно истинно, одно ложно, а третьего не дано. Он действителен только для контрадик­торных (противоречивых) высказываний (А - О, Е - J, О - A, J - Е), которые не могут быть вместе ложными. Сфера применимости этого закона может быть представлена следующими вариантами-схемами:

1. Это S есть Р. - Это S не есть Р.

2. Все S есть Р. - Некоторые S не есть Р.

3. Ни одно S не есть Р. - Некоторые S есть Р.

Законом непротиворечия называется форма (А л А). Она тоже порождает только истинные сложные высказывания Данный закон гласит: два противоположных высказывания не могут быть истин­ными в одно и то же время и в одном и том же отношении. Следова­тельно, одно из них или даже оба могут быть ложными.

Варианты схемы применения данного закона:

1. А - Е. Все S есть Р. - Ни одно S не есть Р (ложно одно из них, или ложны оба высказывания).

2. А - О. Все S есть Р. - Некоторые S не есть Р (ложно одно из

них).

3. Е - J. Ни одно S не есть Р. - Некоторые S есть Р (ложно одно

из них).

4. Это S есть Р. - Это S не есть Р (ложно одно из них).

Согласно закону тождества (А ↔ А), всякое высказывание яв­ляется необходимым и достаточным условием своей собственной истинности. Отсюда вытекает, что в процессе рассуждения всякое высказывание должно быть согласовано с самим собой. Рассогласо­ванность в смыслах используемых высказываний чревата серьезны­ми ошибками. Самые серьезные из них называются подменой поня­тия и подменой тезиса.

Известно, что если отрицать дважды некоторое высказывание, то в результате получается, что утверждается это высказывание без всякого отрицания. Так, говоря: «Неверно, что Иванов не виноват», мы тем самым утверждаем: «Иванов виноват». Отсюда ясна спра­ведливость закона удаления двойного отрицания.

Столь же приемлемо и обратное положение - А → А, называе­мое законом введения двойного отрицания.

Рассмотренные законы с одной переменной легко устанавлива­ются табличным способом (см. табл. 4.1).

Таблица 4.1

 

А	Av Ā	(А Ù А)	А↔А	Ā →А	А→ Ā
И	И	И	И	И	И
л	И	И	И	И	И

Более сложную структуру имеют законы с более чем одной пе­ременной.

Законы исключенного третьего, непротиворечия и тождества бы­ли открыты еще Аристотелем.

Закон достаточного основания был сформулирован Лейбницем уже в XVIII в. Он гласит: всякая мысль должна быть достаточно обоснованной. Смысл этого закона выходит за пределы языка логи­ки высказываний и не может быть представлен в логической форме. Данный закон работает в системе доказательств, опровержения и требует аргументации. Достаточным основанием любого высказы­вания является другое высказывание, ранее признанное истинным из которого с необходимостью вытекает истинность данного выска­зывания. Любое положение может быть признано истинным только после того, как его истинность будет доказана, и не должно прини­маться на веру.

Закон достаточного основания гласит: всякая истинная (доказан­ная) мысль имеет достаточное основание. Выражается он так: «А есть потому, что есть В».

Упражнения

1. Являются ли законами с более чем одной переменной сле­дующие логические формы:

1). (А Ù В) → (В Ù А).

2). (А Ù В) → А. 4). А → (В → (А Ù В)). 6). ((А→ В) Ù А) → В. 8). (AvB) → (BvA). 10). (А ↔ В) → (В ↔ А). 12).(А↔В) → (В->А). 14). (AvB) ↔ (AÙB).

3). (А Ù В) → В.

5). (А→В) → (В→А).

7). (А → В) → (А Ù В).

9). (А Ù В) → (А → В).

11). (А ↔ В) → (А→ В). 13). ((А→ В) Ù (В→ А))

.

2. Определить, к каким из следующих пар имен применим закон исключенного третьего?

1). Революционер, контрреволюционер.

2). Грамотный, неграмотный.

3). Глубокий, мелкий.

4). Доказуемый, недоказуемый.

5). Обратимый, необратимый.

3. С помощью таблиц истинности установить, соответствуют ли логическим законам следующие рассуждения:

1). Если по проводнику проходит электрический ток, то вокруг него образуется магнитное поле. Вокруг проводника образуется магнитное поле, следовательно, по нему проходит электрический ток.

2). Если по проводнику проходит электрический ток, то вокруг него образуется магнитное поле, но по проводнику не проходит электрический ток, следовательно, вокруг него не образуется маг­нитное поле.

3). Если по проводнику проходит электрический ток, то вокруг него образуется магнитное поле, но вокруг проводника не образует­ся магнитное поле, следовательно, по нему не проходит электриче­ский ток.

4. Нарушены ли требования закона тождества в следующих вы­сказываниях:

1). «Ноздрев был в некотором отношении исторический человек. Ни на одном собрании, где он был, не обходилось без истории»

(Н. Гоголь).

2). Спортсмен теряет очки. 3). Он погнал лошадь под гору в карьер. 4). Утром все получили новые наряды.

5). «Почему ваш хор называется смешанным? Ведь поют только женщины. - Потому, что одни петь умеют, а другие - нет».

6). Купец из соображений рекламы вывесил объявление: «Сего­дня - за наличные, завтра - в кредит».

ВЫВОД

Структура и виды выводов

Вывод - форма мышления, посредством которой осуществляется переход от одного или нескольких известных высказываний к ново­му высказыванию.

Исходные высказывания называются посылками вывода, а новое высказывание, вытекающее из сопоставления посылок, - заключе­нием.

По количеству посылок выводы делятся на непосредственные (одна посылка) и опосредованные (более одной посылки), а также на дедуктивные и недедуктивные (вероятностные).

Вывод называется дедуктивным, если из истинных посылок следует истинное заключение. Знание, полученное с помощью де­дуктивного вывода, не может быть более общим, чем то, которое заложено в исходных посылках. Например: «Все металлы - химиче­ские элементы, олово - металл; следовательно, олово - химический

элемент».

В недедуктивном выводе заключение имеет вероятностный ха­рактер. Например: «Железо - твердое тело, медь - твердое тело, зо­лото - твердое тело, платина - твердое тело; вероятно, все металлы -твердые тела».

Правила терминов

1. В простом категорическом силлогизме должно быть только три термина. Наиболее распространенная ошибка, связанная с наруше­нием этого правила, носит наименование «учетверение терминов».

Например:

Лук - оружие дикарей.

Эт о растение- лук._________

Это растение - оружие дикарей.

Ошибка в заключении основана на нарушении требований закона тождества по отношению к среднему термину «лук». Средний тер­мин как бы раздваивается, получается не три, а четыре термина, и связь между крайними терминами пропадает.

2. Средний термин должен быть распределен хотя бы в одной из посылок. Если он не распределен ни в одной из посылок, связь ме­жду крайними терминами остается неопределенной. Например:

Все металлы электропроводны.

Правила посылок

1. Из двух частных посылок не делается заключение.

2.Если одна из посылок - частная, то и заключение должно быть частным.

3. Из двух отрицательных посылок не делается заключение.

4. Если одна из посылок - отрицательная, то и заключение долж­но быть отрицательным.

 

Виды силлогизмов

Кроме простого категорического силлогизма существуют и дру­гие виды силлогизмов (условные, разделительные, условно-разделительные и др.).

 

Условными называются силлогизмы, в которых обе посылки - условные высказывания. Условным является высказывание, имею­щее структуру: «Если А, то В», где А называется основанием, а В - следствием.

Схема условного силлогизма:

Если А, то В.

Если В, то С.

Если А, то С.

 

Вывод в условном силлогизме основывается на правиле: следст­вие следствия есть следствие основания.

Условно-категорическими называются силлогизмы, в которых одна из посылок - условное высказывание, а другая посылка и за­ключение - категорические высказывания. Такой силлогизм может давать как достоверное, так и вероятное знание.

Общая форма силлогизмов, дающих истинное знание:

1. Если А, то В 2. Если А, то В

А Не В

В Не А

 

Общая форма силлогизмов, дающих вероятное знание:
1. Если А, то В. 2. Если А, то В.

В Не А

Вероятно, А. Вероятно, не В.

Например:

 

Разделительным называют силлогизм, в котором посылки и за­ключение являются разделительными высказываниями. Раздели­тельные высказывания имеют структуру: «Либо А, либо В». Разли чают два типа разделительных высказываний: исключающее разделительные и неисключающе-разделителъные. Союз «ли­бо...либо» соединяет в исключающе-разделительном высказывании несовместимые друг с другом высказывания, которые называются альтернативами. Неисключающе-разделительное высказывание состоит из совместимых высказываний, соединяемых союзом «или».

Например:

Каждый телескоп есть или рефрактор, или рефлектор.

Каждый рефлектор - или металлический, или зерка льный.

Телескоп есть или рефрактор, или металлический рефлектор, или зеркальный рефлектор.

Это - разделительный силлогизм, посылки и заключение которо­го содержат альтернативы.

 

Структура разделительного силлогизма может быть представлена схемой:

А есть В или С.

С есть М или Р.

А есть В, или М, или D.

Разделительно-категорическим называется силлогизм, в кото­ром одна из посылок - разделительное высказывание, а другая по­сылка и заключение - категорические высказывания. Такой силло­гизм содержит следующие достоверные структуры:

1). А или В. В. Не А ФффА.

2). А или В. А. Не В.

3). А или В. Не А. В.

4) А или В

Не В.

А

 

Для обеспечения достоверности выбора необходимо, чтобы в разделительном суждении были приведены все возможные альтер­нативы. Другими словами, деление субъекта высказывания должно быть полным, исчерпывающим.

 

Силлогизм, в котором одна из посылок - условное высказывание, а другая - разделительное высказывание, называется условно-разделительным. В зависимости от количества альтернатив, содер­жащихся в разделительном высказывании, различают дилеммы (две альтернативы), трилеммы (три альтернативы), полилеммы (много альтернатив).

Вероятностные выводы

В вероятностных выводах заключение не следует строго логиче­ски из посылок, а лишь в некоторой степени подтверждается ими. По­сылки не являются достаточным основанием для заключения. К таким выводам относятся индуктивные выводы и выводы по аналогии.

Индуктивными называются выводы, когда на основе повто­ряющегося признака у отдельных предметов делается заключение о его принадлежности всем предметам определенного класса.

Различают индукцию полную, если посылки исчерпывают весь класс предметов, подлежащих обобщению, и неполную, если посыл­ки не исчерпывают всего класса предметов, подлежащих индуктив­ному обобщению. Заключением как по полной, так и по неполной индукции является общее высказывание.

Схема вывода по полной индукции:

S1 есть Р.

S2 есть Р.

……….

Sn есть Р.

S1 S2……. Sn исчерпывают все предметы класса S

Следовательно, все S есть P

 

Схема вывода по неполной индукции:

S1 есть Р.

S2 есть Р.

……….

Sn есть Р.

S1 S2……. Sn – элементы класса S

Вероятно, все S есть P

 

Вывод по неполной индукции будет более вероятен при выпол­нении следующих условий:

1) для индуктивного обобщения необходимо брать возможно большее количество элементов определенного класса;

2) факты, служащие основанием обобщения, должны быть раз­нообразны и, по возможности, полно характеризовать предмет обобщения;

3) предметы, знания о которых обобщаются, должны обладать внутренней объективной связью между собой; чем более сущест­венный признак берется в качестве индуктивного обобщения, тем более повышается вероятность вывода.

Неполная индукция может быть популярной (через простое пере­числение признака у определенной группы предметов) и научной (через отыскание существенных, причинно-следственных связей

предметов).

В логике разработаны следующие методы установления причин­ной связи между предметами: метод сходства, метод различия, ме­тод сопутствующих изменений, метод остатков.

Метод сходства: если два или более случаев изучаемого явле­ния имеют общим лишь одно обстоятельство, то, очевидно, оно и есть причина данного явления. Например:

При условиях ABC возникает а.

При условиях МЕВ возникает а.

При условиях МВС возникает а.

Вероятно, В есть причина а.;

Метод различия: если случаи, при которых явление наступает или не наступает, различаются