
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиляСодержание книги
Поиск на нашем сайте
Якщо хвилі, поширюючись в пружному середовищі з кінцевою швидкістю, переносять енергію, то вони називаються біжучими. Перенесення енергії в хвильовому русі кількісно характеризується вектором густини потоку енергії. Вектор потоку енергії вперше для механічних пружних хвиль був введений російським фізиком Умовим і називається вектором Умова. Напрямок вектора Умова збігається з напрямком перенесення енергії, а його модуль дорівнює енергії, яка переноситься хвилею через одиничну площадку, розташовану перпендикулярно до напрямку поширення хвилі, за одиницю часу. Для одержання рівняння біжучої хвилі ─ залежності зміщення коливної точки пружного середовища від координати і часу ─ розглянемо плоску синусоїдальну хвилю, допустивши, що вісь х збігається з напрямком поширення хвилі (рис. 21). У даному випадку хвильові поверхні, тобто поверхні однакової фази, перпендикулярні до осі х, а тому всі точки пружного середовища на цих поверхнях коливаються однаково. Зміщення будь-якої точки пружного середовища від положення рівноваги в цьому випадку залежить лише від координати х і часу t, а його величина буде дорівнювати Розглянемо деяку точку В, якаперебуває на відстані х від джерела коливань (рис. 1). Якщо коливання точок пружного середовища, які лежать у площині х = 0, описуються функцією U(0,t) = A cos
де А – максимальне зміщення виділеної коливної точки В від положення рівноваги; ω – циклічна частота генератора коливань джерела. Рівняння (2) є рівнянням біжучої хвилі. Якщо плоска хвиля поширюється в протилежному напрямку, то
В загальному випадку рівнянням плоскої синусоїдальної хвилі, яка поширюється без поглинання енергії уздовж позитивного напрямку осі х, має вигляд
де А – амплітуда хвилі; ω – циклічна частота хвилі;
[ω (t - x/υ) + φ0] – фаза плоскої хвилі.
В рівнянні (3) синусоїдальний характер хвилі характеризують хвильовим числом, яке дорівнює
З врахуванням (4) рівняння (3) матиме вигляд
Рівняння хвилі, яка поширюється в сторону менших значень осі х, відрізняється від (5) тільки знаком члена kх. Розглянемо випадок, коли в процесі хвильового руху фаза коливань не змінюється з часом, тобто
Диференціюємо вираз (6) за часом, одержимо
звідки
Отже, швидкість υпоширення хвилі в рівнянні (6) є не що інше, як швидкість переміщення фази хвилі, а тому її називають фазовою швидкістю. Сферичні хвилі утворюються в однорідному і ізотропному середовищі від точкових джерел коливань. Якщо повторити хід міркувань для плоскої хвилі, можна показати, що рівняння сферичної синусоїдальної хвилі, хвилі, хвильові поверхні якої мають вигляд концентричних сфер, записується так
де r –відстань від точкового джерела сферичних хвиль до виділеної точки пружного середовища. У випадку сферичної хвилі навіть у середовищі, яке не поглинаєенергії, амплітуда коливань не залишається постійною, а зменшується з відстанню за законом З рівняння (3) можна одержати, що
тобто фазова швидкість синусоїдальних хвиль залежить від їхньої частоти. Це явище називають дисперсією хвиль, а середовище, у якому спостерігається дисперсія хвиль, називається дисперсним середовищем.
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.172.11 (0.006 с.) |


 , то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х необхідний час τ =
, то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х необхідний час τ =  , де
, де 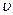 – швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х, буде мати вигляд
– швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х, буде мати вигляд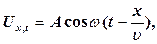 (2)
(2)
 (3)
(3)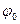 –початкова фаза коливань, обумовлена вибором початкових значень х і t;
–початкова фаза коливань, обумовлена вибором початкових значень х і t; (4)
(4) (5)
(5) (6)
(6) ,
,
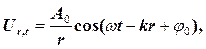 (7)
(7) Рівняння (7) має місце лише для великих r, які значно перевищують розміри джерела коливань (джерело коливань тут можна вважати точковим).
Рівняння (7) має місце лише для великих r, які значно перевищують розміри джерела коливань (джерело коливань тут можна вважати точковим).



