Слайд 2. Природні і штучні фрактали.

Фрактали в природі фрактал Мандельброта штучний фрактал   крива Коха крива Гільберта

 

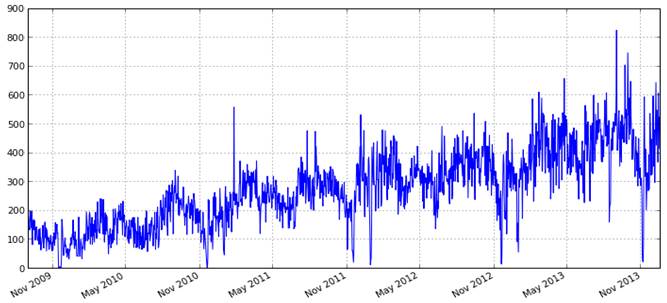
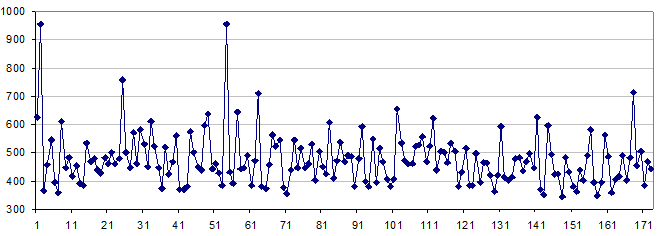
Різні природні та штучні фрактали приведені на цьому слайді. До фракталів відносять також і часові ряди. На слайді 3 приведені типові зображення часових рядів. Основними фрактальними характеристиками часових рядів є фрактальна розмірність та показник Герста. Останнім часом зустрічаються статті, в яких використовують індекс фрактальності та розмірність мінімального покриття

Слайд 3. Зображення часових рядів

 

Фрактальний характер мають стохастичні та хаотичні часові ряди. Основними показниками таких часових рядів, а також багатьох інших, фрактальна розмірність та показник Герста.

Між цими двома показниками існує, виявлена В. Мандельбротом проста залежність: значення фрактальної розмірності рівне два мінус значення показника Герста, тобто .

На сьогоднішній день має місце така методика: спочатку знайти значення показника Герста і далі знайти значення фрактальної розмірності. Проте існує певне протиріччя – показник Герста визначається емпіричним шляхом, а визначення фрактальної розмірності хоча і має теоретичну базу є вельми трудомістким.

 

Слайд 4. Актуальність дослідження

Актуальність дослідження

– фрактальна розмірність

 

– показник Герста

 

чи ?

Актуальною науково-прикладною задачею

є розробка методу точного визначення фрактальної розмірності клітинковим методом в доступному програмному середовищі.

 

Зв'язок цих двох показників створює певне протиріччя: переважаюча більшість дослідників визначають фрактальну розмірність, яка є строго і однозначно визначеним математичним об’єктом, через емпіричну формулу показника Герста, що має безліч варіантів з необґрунтованими умовами, і отримують і різних випадках різне емпіричне значення фрактальної розмірності, проте, визначивши точно значення фрактальної розмірності досить просто визначити єдине і точне значення показника Герста.

Більшість дослідників вважають, що визначення фрактальної розмірності є рутинним і не точним і тому схиляються до визначення показника Герста фактично будь-яким прийнятним для них методом.

Використання клітинкового методу для визначення фрактальної розмірності клітинковим методом дійсно дає неточне її значення, оскільки враховуються не повністю заповнені клітинки.

 

 

Слайд 5.1. Характеристика досліджень

Характеристика досліджень

Об’єктом дослідження є фрактальні характеристики.

Предметом дослідження є надані, експериментально отримані часові

ряди, клітинковий метод визначення фрактальної розмірності, метод

визначення показника Герста.

Вихідними даними є наукові публікації, ключові слова та концепція роботи.

Методи дослідження: теорія ймовірностей та математична статистика,

методологія системного підходу та методи фрактального аналізу

Слайд 5.2. Мета роботи

Мета роботи: розробити інформаційну технологію для реалізації фрактального аналізу часових рядів в середовищі Ексель. Для досягнення поставленої мети необхідно розв’язати такі задачі. 1. Розробити концепцію організації магістерського дослідження клітинкового методу визначення фрактальної розмірності. 2. Розробити метод усунення головного недоліку клітинкового методу. 3. Визначити показники Герста за методикою Герста-Федера. 4. Визначити показники Герста за методикою Петерса. 5. Визначити індекс фрактальності та розмірність мінімального покриття.