Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Алгебраический метод решения текстовых задач
План
1. Общие замечания к решению задач алгебраическим методом. 2. Задачи на движение. 3. Задачи на работу. 4. Задачи на смеси и проценты. 5. Использование алгебраического метода для нахождения арифметического пути решения текстовых задач.
1. При решении задач алгебраическим методом искомые величины или другие величины, зная которые можно определить искомые, обозначают буквами (обычно х, у, z). Все независимые между собой соотношения между данными и неизвестными величинами, которые либо непосредственно сформулированы в условии (в словесной форме), либо вытекают из смысла задачи (например, физические законы, которым подчиняются рассматриваемые величины), либо следуют из условия и некоторых рассуждений, записываются в виде равенства неравенств. В общем случае эти соотношения образуют некоторую смешанную систему. В частных случаях эта система может не содержать неравенств либо уравнений или она может состоять лишь из одного уравнения или неравенства. Решение задач алгебраическим методом не подчиняется какой-либо единой, достаточно универсальной схеме. Поэтому всякое указание, относящееся ко всем задачам, носит самый общий характер. Задачи, которые возникают при решении практических и теоретических вопросов, имеют свои индивидуальные особенности. Поэтому их исследование и решение носят самый разнообразный характер. Остановимся на решении задач, математическая модель которых задается уравнением с одним неизвестным. Напомним, что деятельность по решению задачи состоит из четырех этапов. Работа на первом этапе (анализ содержания задачи) не зависит от выбранного метода решения и не имеет принципиальных отличий. На втором этапе (при поиске пути решения задачи и составлении плана ее решения) в случае применения алгебраического метода решения осуществляются: выбор основного соотношения для составления уравнения; выбор неизвестного и введение обозначения для него; выражение величин, входящих в основное соотношение, через неизвестное и данные. Третий этап (осуществление плана решения задачи) предполагает составление уравнения и его решение. Четвертый этап (проверка решения задачи) осуществляется стандартно. Обычно при составлении уравнений с одним неизвестным х придерживаются следующих двух правил.
Правило I. Одна из данных величин выражается через неизвестное х и другие данные (то есть составляется уравнение, в котором одна часть содержит данную величину, а другая – ту же величину, выраженную посредством х и других данных величин). ПравилоII. Для одной и той же величины составляются два алгебраических выражения, которые затем приравниваются друг к другу. Внешне кажется, что первое правило проще второго. В первом случае всегда требуется составить одно алгебраическое выражение, а во втором – два. Однако часто встречаются задачи, в которых удобнее составить два алгебраических выражения для одной и той же величины, чем выбрать уже известную и составить для нее одно выражение. Процесс решения текстовых задач алгебраическим способом выполняется по следующему алгоритму: 1. Сначала выбирают соотношение, на основании которого будет составлено уравнение. Если задача содержит более двух соотношений, то за основу для составления уравнения надо взять то соотношение, которое устанавливает некоторую связь между всеми неизвестными. 2. Затем выбирают неизвестное, которое обозначают соответствующей буквой. 3. Все неизвестные величины, входящие в выбранное для составления уравнения соотношение, необходимо выразить через выбранное неизвестное, опираясь на остальные соотношения, входящие в задачу кроме основного.
Центральное место среди перечисленных операций занимает выбор основного соотношения для составления уравнений. Рассмотренные примеры показывают, что выбор основного соотношения является определяющим при составлении уравнений, вносит логичную стройность в порою расплывчатый словесный текст задачи, дает уверенность в ориентации и предохраняет от беспорядочных действий для выражения всех входящих в задачу величин через данные и искомые. Алгебраический метод решения задач имеет огромное практическое значение. С его помощью решают самые разнообразные задачи из области техники, сельского хозяйства, быта. Уже в средней школе уравнения применяются учащимися при изучении физики, химии, астрономии. Там, где арифметика оказывается бессильной или, в лучшем случае, требует крайне громоздких рассуждений, там алгебраический метод легко и быстро приводит к ответу. И даже в так называемых «типовых» арифметических задачах, сравнительно легко решаемых арифметическим путем, алгебраическое решение, как правило, является и более коротким, и более естественным.
Алгебраический метод решения задач позволяет легко показать, что некоторые задачи, отличающиеся друг от друга лишь фабулой, имеют не только одни и те же соотношения между данными и искомыми величинами, но и приводят к типичным рассуждениям, посредством которых устанавливаются эти соотношения. Такие задачи дают лишь различные конкретные интерпретации одного и того же математического рассуждения, одних и тех же соотношений, то есть имеют одну и ту же математическую модель. 2. К группе задач на движение относятся задачи, в которых говорится о трех величинах: пути (s), скорости (v) и времени (t). Как правило, в них речь идет о равномерном прямолинейном движении, когда скорость постоянна по модулю и направлению. В этом случае все три величины связаны следующим соотношением: S = vt. Например, если скорость велосипедиста 12 км/ч, то за 1,5 ч. он проедет 12 км/ч × 1,5 ч = 18 км. Встречаются задачи, в которых рассматривается равноускоренное прямолинейное движение, то есть движение с постоянным ускорением (а). Пройденный путь s в этом случае вычисляется по формуле: S = v0t + at2/2, где v0 – начальная скорость движения. Так, за 10 с падения с начальной скоростью 5 м/с и ускорением свободного падения 9,8 м2/с тело пролетит расстояние, равное 5 м/с × 10с + 9,8 м2/с × 102с2/2 = 50 м + 490 м = 540 м. Как уже отмечалось, в ходе решения текстовых задач и в первую очередь в задачах, связанных с движением, весьма полезно сделать иллюстративный чертеж (построить вспомогательную графическую модель задачи). Чертеж следует выполнить так, чтобы на нем была видна динамика движения со всеми встречами, остановками и поворотами. Грамотно составленный чертеж позволяет не только глубже понять содержание задачи, но и облегчает составление уравнений и неравенств. Примеры таких чертежей будут приведены ниже. Обычно в задачах на движение принимаются следующие соглашения. 1. Если специально не оговорено в задаче, то движение на отдельных участках считается равномерным (будь то движение по прямой или по окружности). 2. Повороты движущихся тел считаются мгновенными, то есть происходят без затрат времени; скорость при этом также меняется мгновенно. Данную группу задач, в свою очередь, можно разбить на задачи, в которых рассматриваются движения тел: 1) навстречу друг другу; 2) в одном направлении («вдогонку»); 3) в противоположных направлениях; 4) по замкнутой траектории; 5) по течению реки. 1. Если расстояние между телами равно S, а скорости тел равны v1 и v 2 (рис. 16 а), то при движении тел навстречу друг другу время, через которое они встретятся, равно S/(v1 + v 2). 2. Если расстояние между телами равно S, а скорости тел равны v 1 и v 2 (рис. 16 б), то при движении тел в одну сторону (v 1 > v 2) время, через которое первое тело догонит второе, равно S/(v1 – v 2).
3. Если расстояние между телами равно S, а скорости тел равны v 1 и v 2 (рис. 16 в), то, отправившись одновременно в противоположных направлениях, тела будут через время t находиться на расстоянии S 1 = S + (v 1 + v2)t.
Рис. 16 4. Если тела движутся в одном направлении по замкнутой траектории длиной s со скоростями v 1 и v 2, то время, через которое тела опять встретятся (одно тело догонит другое), отправившись одновременно из одной точки, находится по формуле t = S/(v1 – v 2) при условии, что v 1 > v 2. Это следует из того, что при одновременном старте по замкнутой траектории в одном направлении тело, скорость которого больше, начинает догонять тело, скорость которого меньше. В первый раз оно догоняет его, пройдя расстояние на S большее, чем другое тело. Если же оно обгоняет его во второй, в третий раз и так далее, это означает, что оно проходит расстояние на 2 S, на 3 S и так далее большее, чем другое тело. Если тела движутся в разных направлениях по замкнутой траектории длиной S со скоростями v 1 и v 2, то время, через которое они встретятся, отправившись одновременно из одной точки, находится по формуле t = v (v 1 + v 2). В этом случае сразу после начала движения возникает ситуация, когда тела начинают двигаться навстречу друг другу. 5. Если тело движется по течению реки, то его скорость относительно берега и слагается из скорости тела в стоячей воде v и скорости течения реки w: и = v + w. Если тело движется против течения реки, то его скорость и = v – w. Например, если скорость катера v = 12 км/ч, а скорость течения реки w = 3 км/ч, то за 3 ч. по течению реки катер проплывет (12 км/ч + 3 км/ч) × 3 ч. = 45 км, а против течения – (12 км/ч – 3 км/ч) × 3 ч. = 27 км. Считают, что скорость предметов, имеющих нулевую скорость движения в стоячей воде (плот, бревно и т. п.), равна скорости течения реки. Рассмотрим несколько примеров. Пример. Из одного пункта в одном направлении через каждые 20 мин. выезжают автомобили. Второй автомобиль едет со скоростью 60 км/ч, а скорость первого на 50% больше скорости второго. Найдите скорость движения третьего автомобиля, если известно, что он обогнал первый автомобиль на 5,5 ч позже, чем второй. Решение. Пусть х км/ч – скорость третьего автомобиля. Скорость первого автомобиля на 50% больше скорости второго, значит, она равна
При движении в одном направлении время встречи находится как отношение расстояния между объектами к разности их скоростей. Первый автомобиль за 40 мин. (2/3 ч) проедет 90 × (2/3) = 60 км. Следовательно, третий его догонит (они встретятся) через 60/(х – 90) часов. Второй за 20 мин. (1/3 ч) проедет 60 × (1/3) = 20 км. Значит, третий его догонит (они встретятся) через 20/(х – 60) ч. (рис. 17).
Рис.17
Рис. 17
После несложных преобразований получим квадратное уравнение 11х2 – 1730х + 63000 = 0, решив которое найдем Проверка показывает, что второй корень не удовлетворяет условию задачи, так как в этом случае третий автомобиль не догонит другие автомобили. Ответ: скорость движения третьего автомобиля 100 км/ч. Пример. Теплоход прошел по течению реки 96 км, вернулся обратно и некоторое время простоял под погрузкой, затратив на все 32 ч. Скорость течения реки равна 2 км/ч. Определите скорость теплохода в стоячей воде, если время погрузки составляет 37,5% от времени, затраченного на весь путь туда и обратно. Решение. Пусть х км/ч – скорость теплохода в стоячей воде. Тогда (х + 2) км/ч – его скорость по течению; (х – 2) км/ч – против течения; 96/(х + 2) ч. – время движения по течению; 96/(х – 2) ч. – время движения против течения. Так как 37,5% от общего количества времени теплоход стоял под погрузкой, то чистое время движения равно 62,5% × 32/100% = 20 (ч.). Следовательно, по условию задачи имеем уравнение:
Преобразовав его, получим: 24(х – 2 + х + 2) = 5(х + 2)(х – 2) => 5 х 2 – 4 х – 20 = 0. Решив квадратное уравнение, находим: х 1 = 10; х2 = -0,4. Второй корень не удовлетворяет условию задачи. Ответ: 10 км/ч – скорость движения теплохода в стоячей воде. Пример. Автомобиль проехал путь из города А в город С через город В без остановок. Расстояние АВ, равное 120 км, он проехал с постоянной скоростью на 1 ч. быстрее, чем расстояние ВС, равное 90 км. Определите среднюю скорость движения автомобиля от города А до города С, если известно, что скорость на участке АВ на 30 км/ч больше скорости на участке ВС. Решение. Пусть х км/ч – скорость автомобиля на участке ВС. Тогда (х + 30) км/ч – скорость на участке АВ, 120/(х + 30) ч, 90/ х ч – время, за Следовательно, по условию задачи имеем уравнение:
Преобразуем его: 120 х + 1(х + 30) х = 90(х + 30) => х2 + 60 х – 2700 = 0. Решив квадратное уравнение, находим: х1 = 30, х2 = -90. Второй корень не удовлетворяет условию задачи. Значит, скорость на участке ВС равна 30 км/ч, на участке АВ – 60 км/ч. Отсюда следует, что расстояние АВ автомобиль проехал за 2 ч. (120 км: 60 км/ч = 2 ч.), а расстояние ВС – за 3 ч. (90 км: 30 км/ч = 3 ч.), поэтому все расстояние АС он проехал за 5 ч. (3 ч. + 2 ч. = 5 ч.). Тогда средняя скорость движения на участке АС, протяженность которого 210 км, равна 210 км: 5 ч. = 42 км/ч. Ответ: 42 км/ч – средняя скорость движения автомобиля на участке АС. 2.К группе задач на работу относятся задачи, в которых говорится о трех величинах: работе А, времени t, в течение которого производится работа, производительности Р – работе, произведенной в единицу времени. Эти три величины связаны уравнением А = Рt. К задачам на работу относят и задачи, связанные с наполнением и опорожнением резервуаров (сосудов, баков, бассейнов и т. п.) с помощью труб, насосов и других приспособлений. В качестве произведенной работы в этом случае рассматривают объем перекачанной воды.
Задачи на работу, вообще говоря, можно отнести к группе задач на движение, так как в задачах такого типа можно считать, что вся работа или полный объем резервуара играют роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения. Однако по фабуле эти задачи естественным образом различаются, причем часть задач на работу имеют свои специфические приемы решения. Так, в тех задачах, в которых объем выполняемой работы не задан, вся работа принимается за единицу. Пример. Две бригады должны были выполнить заказ за 12 дней. После 8 дней совместной работы первая бригада получила другое задание, поэтому вторая бригада заканчивала выполнение заказа еще 7 дней. За сколько дней могла бы выполнить заказ каждая из бригад, работая отдельно? Решение. Пусть первая бригада выполняет задание за х дней, вторая бригада – за y дней. Примем всю работу за единицу. Тогда 1/ х – производительность первой бригады, a 1/ y – второй. Так как две бригады должны выполнить заказ за 12 дней, то получим первое уравнение 12(1/ х + 1/ у) = 1. Из второго условия следует, что вторая бригада работала 15 дней, а первая – только 8 дней. Значит, второе уравнение имеет вид: 8/ х + 15/ у = 1. Таким образом, имеем систему:
Вычтем из второго уравнения первое, получим: 21/ y = 1 => у = 21. Тогда 12/ х + 12/21 = 1 => 12/ х – = 3/7 => х = 28. Ответ: за 28 дней выполнит заказ первая бригада, за 21 день – вторая. Пример. Рабочий А и рабочий В могут выполнить работу за 12 дней, рабочий А и рабочий С – за 9 дней, рабочий В и рабочий С – за 12 дней. За сколько дней они выполнят работу, работая втроем? Решение. Пусть рабочий А может выполнить работу за х дней, рабочий В – за у дней, рабочий С – за z дней. Примем всю работу за единицу. Тогда 1/ х, 1/y и 1/ z – производительности рабочих А, В и С соответственно. Используя условие задачи, приходим к следующей системе уравнений, представленной в таблице.
Таблица 1
Сложив почленно уравнения системы, получим:
Сумма
Ответ: 7,2 дня. Пример. В бассейн проведены две трубы – подающая и отводящая, причем через первую трубу бассейн наполняется на 2 ч дольше, чем через вторую вода из бассейна выливается. При заполненном на одну треть бассейне были открыты обе трубы, и бассейн оказался пустым спустя 8 ч. За сколько часов через одну первую трубу может наполниться бассейн и за сколько часов через одну вторую трубу может осушиться полный бассейн? Решение. Пусть V м3 – объем бассейна, х м3/ч – производительность подающей трубы, у м3/ч – отводящей. Тогда V/x ч. – время, необходимое подающей трубе для заполнения бассейна, V/y ч. – время, необходимое отводящей трубе на осушение бассейна. По условию задачи V/x – V/y = 2. Так как производительность отводящей трубы больше производительности наполняющей, то при включенных обеих трубах будет происходить осушение бассейна и одна треть бассейна осушится за время (V/3)/(y – x), которое по условию задачи равно 8 ч. Итак, условие задачи может быть записано в виде системы двух уравнений с тремя неизвестными:
В задаче необходимо найти V/x и V/y. Выделим в уравнениях комбинацию неизвестных V/x и V/y, записав систему в виде:
Вводя новые неизвестные V/x = а и V/y = b, получаем следующую систему:
Подставляя во второе уравнение выражение а = b + 2, имеем уравнение относительно b:
решив которое найдем b1 = 6, b2= -8. Условию задачи удовлетворяет первый корень 6, = 6 (ч.). Из первого уравнения последней системы находим а = 8 (ч), то есть первая труба наполняет бассейн за 8 ч. Ответ: через первую трубу бассейн наполнится через 8 ч., через вторую трубу бассейн осушится через 6 ч. Пример. Одна тракторная бригада должна вспахать 240 га, а другая на 35% больше, чем первая. Первая бригада, вспахивая ежедневно на 3 га меньше второй, закончила работу на 2 дня раньше, чем вторая бригада. Сколько гектаров вспахивала каждая бригада ежедневно? Решение. Найдем 35 % от 240 га: 240 га × 35 % /100 % = 84 га. Следовательно, вторая бригада должна была вспахать 240 га + 84 га = 324 га. Пусть первая бригада вспахивала ежедневно х га. Тогда вторая бригада вспахивала ежедневно (х + 3) га; 240/ х – время работы первой бригады; 324/(х + 3) – время работы второй бригады. По условию задачи первая бригада закончила работу на 2 дня раньше, чем вторая, поэтому имеем уравнение
которое после преобразований можно записать так: 324 х – 240 х – 720 = 2х2 + 6х => 2х2 – 78х + 720 = 0 => х2 – 39х + 360 = 0. Решив квадратное уравнение, находим х1 = 24, х2 = 15. Это норма первой бригады. Следовательно, вторая бригада вспахивала в день 27 га и 18 га соответственно. Оба решения удовлетворяют условию задачи. Ответ: 24 га в день вспахивала первая бригада, 27 га – вторая; 15 га в день вспахивала первая бригада, 18 га – вторая. Пример. В мае два цеха изготовили 1080 деталей. В июне первый цех увеличил выпуск деталей на 15%, а второй увеличил выпуск деталей на 12%, поэтому оба цеха изготовили 1224 детали. Сколько деталей изготовил в июне каждый цех? Решение. Пусть х деталей изготовил в мае первый цех, у деталей – второй. Так как в мае изготовлено 1080 деталей, то по условию задачи имеем уравнение x + y = 1080. Найдем 15% от х:
Итак, на 0,15 х деталей увеличил выпуск продукции первый цех, следовательно, в июне он выпустил х + 0,15 х = 1,15 x деталей. Аналогично найдем, что второй цех в июне изготовил 1,12 y деталей. Значит, второе уравнение будет иметь вид: 1,15 x + 1,12 у = 1224. Таким образом, имеем систему:
из которой находим х = 480, у = 600. Следовательно, в июне цеха изготовили 552 детали и 672 детали соответственно. Ответ: первый цех изготовил 552 детали, второй – 672 детали.
4. К группе задач на смеси и процентыотносятся задачи, в которых речь идет о смешении различных веществ в определенных пропорциях, а также задачи на проценты. Задачи на концентрацию и процентное содержание Уточним некоторые понятия. Пусть имеется смесь из п различных веществ (компонентов) А1 А2,..., Аn соответственно, объемы которых равны V1, V2,..., Vn. Объем смеси V0 складывается из объемов чистых компонентов: V0= V1 + V2 +... + Vn. Объемной концентрацией вещества Аi (i = 1, 2,..., п) в смеси называется величина с i, вычисляемая по формуле:
Объемным процентным содержанием вещества Аi (i = 1, 2,..., п) в смеси называется величина pi, вычисляемая по формуле рi = сi, × 100%. Концентрации с1, с2,..., с n, являющиеся безразмерными величинами, связаны равенством с1 + с2 +... + сn = 1, а соотношения
показывают, какую часть полного объема смеси составляют объемы отдельных компонентов. Если известно процентное содержание i -го компонента, то его концентрация находится по формуле:
то есть Pi – это концентрация i -го вещества в смеси, выраженная в процентах. Например, если процентное содержание вещества составляет 70%, то его соответствующая концентрация равна 0,7. И наоборот, если концентрация равна 0,33, то процентное содержание равно 33%. Таким образом, сумма р 1 + р2 + …+ рn = 100%. Если известны концентрации с1 , с2,..., сn компонентов, составляющих данную смесь объема V0, то соответствующие объемы компонентов находятся по формулам:
Аналогичным образом вводятся понятия весовые (массовые) концентрации компонентов смеси и соответствующие процентные содержания. Они определяются как отношение веса (массы) чистого вещества Аi, в сплаве к весу (массе) всего сплава. О какой концентрации, объемной или весовой, идет речь в конкретной задаче, всегда ясно из ее условия. Встречаются задачи, в которых приходится пересчитывать объемную концентрацию на весовую или наоборот. Для того чтобы это сделать, необходимо знать плотности (удельные веса) компонентов, составляющих раствор или сплав. Рассмотрим для примера двухкомпонентную смесь с объемными концентрациями компонентов с1 и с2 (с1 + с2 = 1) и удельными весами компонентов d1 и d2. Масса смеси может быть найдена по формуле:
в которой V1 и V2 – объемы составляющих смесь компонентов. Весовые концентрации компонентов находятся из равенств:
которые определяют связь этих величин с объемными концентрациями. Как правило, в текстах таких задач встречается одно и то же повторяющееся условие: из двух или нескольких смесей, содержащих компоненты A1, A2, А3,..., Аn, составляется новая смесь путем перемешивания исходных смесей, взятых в определенной пропорции. При этом требуется найти, в каком отношении компоненты А1, А2, А3,..., Аn войдут в получившуюся смесь. Для решения этой задачи удобно ввести в рассмотрение объемное или весовое количество каждой смеси, а также концентрации составляющих ее компонентов А1, А2, А3,..., Аn. С помощью концентраций нужно «расщепить» каждую смесь на отдельные компоненты, а затем указанным в условии задачи способом составить новую смесь. При этом легко подсчитать, какое количество каждого компонента входит в получившуюся смесь, а также полное количество этой смеси. После этого определяются концентрации компонентов А1, А2, А3,..., Аn в новой смеси. Пример. Имеются два куска сплава меди и цинка с процентным содержанием меди 80% и 30% соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив взятые куски вместе, получить сплав, содержащий 60% меди? Решение. Пусть первого сплава взято х кг, а второго – у кг. По условию концентрация меди в первом сплаве равна 80/100 = 0,8, во втором – 30/100 = 0,3 (ясно, что речь идет о весовых концентрациях), значит, в первом сплаве 0,8 х кг меди и (1 – 0,8) х = 0,2 х кг цинка, во втором – 0,3 у кг меди и (1 – 0,3) y = 0,7 у кг цинка. Количество меди в получившемся сплаве равно (0,8 × х + 0,3 × у) кг, а масса этого сплава составит (х + у) кг. Поэтому новая концентрация меди в сплаве, согласно определению, равна
По условию задачи эта концентрация должна равняться 0,6. Следовательно, получаем уравнение:
Данное уравнение содержит два неизвестных х и у. Однако по условию задачи требуется определить не сами величины х и у, а только их отношение. После несложных преобразований получаем
Ответ: сплавы надо взять в отношении 3: 2. Пример. Имеются два раствора серной кислоты в воде: первый – 40%-ный, второй – 60%-ный. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили 20%-ный раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-ного раствора, то получили бы 70%-ный раствор. Сколько было 40%-ного и 60%-ного растворов? Решение. Пусть х кг – масса первого раствора, у кг – второго. Тогда масса 20%-ного раствора (х + у + 5) кг. Так как в х кг 40%-ного раствора содержится 0,4 х кг кислоты, в у кг 60%-ного раствора содержится 0,6 y кг кислоты, а в (х + у + 5) кг 20%-ного раствора содержится 0,2(х + у + 5) кг кислоты, то по условию имеем первое уравнение 0,4 х + 0,6 y = 0,2(х +у + 5). Если вместо 5 кг воды добавить 5 кг 80%-ного раствора, то получится раствор массой (х + у + 5) кг, в котором будет (0,4 х + 0,6 у + 0,8 × 5) кг кислоты, что составит 70% от (х + у + 5) кг. Значит, второе уравнение запишется в виде:
Таким образом, получили следующую систему двух уравнений с двумя неизвестными:
решив которую найдем: х = 1, у = 2. Ответ: первый раствор весит 1 кг, второй – 2 кг. Пример. Влажность свежескошенной травы составляет 80%. Влажность полученного из нее сена равна 10%. Сколько нужно скосить травы, чтобы получить 2 т сена? Решение. Так как влажность сена равна 10%, на сухое вещество в нем приходится 90%. Значит, в 2 т сена находится
из которой находим Ответ: надо накосить 9 т травы. Пример. Имеются два сплава золота и серебра. В одном сплаве количество этих металлов находится в отношении 3: 5, а в другом – в отношении 1: 3. Сколько нужно взять каждого сплава, чтобы получить 20 кг нового сплава, в котором золото и серебро находились бы в отношении 3: 7? Решение. Пусть первого сплава нужно взять х кг, а второго – у кг. Согласно условию задачи составим таблицу.
Таблица 2
решив которую найдем х = 8, у = 12. Ответ: нужно взять 8 кг первого сплава и 12 кг второго сплава. Пример. Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, второй – 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите массу олова в новом сплаве. Решение: Пусть х кг – масса олова в новом сплаве, у кг – масса цинка в первом сплаве. Так как новый сплав весит 400 кг и в нем 30% цинка, то он содержит цинка 30 = 120 (кг). Тогда во втором сплаве цинка (120 – у) кг (рис. 18 а). По условию процентное содержание цинка в первом и втором сплавах одинаково, следовательно, получаем уравнение
решив которое, найдем у = 45 (кг). Следовательно, цинка во втором сплаве 120 – 45 = 75 (кг). Так как первый сплав содержит 40% олова, то в 150 кг этого сплава будет 60 (кг), а значит, во втором сплаве олова будет (х – 60) кг. Так как второй сплав содержит 26% меди, то в 250 кг этого сплава меди будет
Рис. 18
Итак, содержание металлов в сплавах теперь такое, как показано на рисунке 18 б. Видим, что во втором сплаве, который весит 250 кг, содержится 75 кг цинка, 65 кг меди, (х – 60) кг олова, поэтому имеет место уравнение 75 + 65 + (х – 60) = 250, решив которое найдем х = 170. Ответ: в новом сплаве содержится 170 кг олова.
5. Среди распространенных методов решения текстовых задач важное значение имеет арифметический метод. Он способствует развитию логического мышления, его гибкости и оригинальности, формированию таких умственных действий, как анализ и синтез. Однако в некоторых случаях бывает непросто сразу найти арифметическое решение задачи. Реальную помощь в такой ситуации может оказать алгебраический метод, с помощью которого, получив ответ на требование задачи, можно попытаться отыскать и ее арифметическое решение. Предварительно сделаем несколько замечаний. Не всегда (и даже далеко не всегда) текстовая задача, решаемая алгебраическим методом, может быть решена арифметически. Как правило, задачи, в ходе решения которых получаются квадратные уравнения или уравнения высших степеней, арифметическим методом решить нельзя. Если при решении задачи алгебраическим методом ее модель сводится к линейному уравнению или системе линейных уравнений, то можно построить и ее арифметическую модель, то есть можно решить задачу, применяя арифметический метод. Вид линейного уравнения, вообще говоря, не всегда «подсказывает» арифметический путь решения задачи, однако дальнейшие преобразования уравнения позволяют его найти. При этом, составив уравнение и решая его, в некоторых случаях можно арифметические действия между данными только намечать, но не выполнять. Тогда найденное для неизвестного числовое выражение будет фактически арифметической моделью данной задачи. Затем необходимо лишь сформулировать вопросы, чтобы записать решение задачи по действиям. Однако как раз именно это сделать бывает нелегко. Нужен определенный опыт установления такой связи между данными методами решения. Решение системы линейных уравнений практически сразу дает возможность наметить ход рассуждений для решения задачи арифметическим методом. Пример. В 8 ч утра из пункта А в пункт В вышел поезд со скоростью 60 км/ч. В 11 ч из пункта В ему навстречу вышел другой поезд со скоростью 70 км/ч. В какое время поезда встретятся, если расстояние между пунктами 440 км. Алгебраический метод приводит к следующему уравнению: (60 + 70) х + 60 × 3 = 440, или 130 х + 180 = 440, где х ч – время движения второго поезда до встречи. Тогда 130 х = 440 – 180 => => 130 х = 260 => х = 2 (ч.). Проделанные рассуждения и выкладки «подсказывают» следующий арифметический путь решения задачи. Найдем: сумму скоростей поездов (60 + 70 = 130); время движения первого поезда до начала движения второго поезда (11 – 8 = 3); расстояние, пройденное первым поездом за 3 ч. (60 × 3 = 180); расстояние, которое осталось пройти поездам до встречи (440 – 80 = 260); время движения второго поезда до встречи (260: 130 = 2). Этапы решения задач алгебраическим и арифметическим методами будем параллельно записывать в таблице 3. Эта таблица позволит наглядно проследить, как алгебраические преобразования в ходе решения уравнений, являющихся моделью текстовой задачи, помогают найти ее арифметическое решение. Таблица 3
Оформим решение задачи арифметическим методом: 1) 11 – 8 = 3 (ч.) – был в пути первый поезд до начала движения второго; 2) 60 × 3 = 180 (км) – прошел первый поезд за 3 ч; 3) 440 – 180 = 260 (км) – расстояние, пройденное поездами при одновременном движении; 4) 60 + 70 = 130 (км/ч) – скорость сближения поездов; 5) 260: 130 = 2 (ч.) – время движения второго поезда; 6) 11 + 2 = 13 (ч) – в такое время поезда встретятся. Ответ: поезда встретятся в 13 ч. Пример. Школьники купили 4 книги, после чего у них осталось 40 р. Если бы они купили 7 таких же книг, то у них осталось бы 16 р. Сколько стоит одна книга? Алгебраический метод приводит к следующему уравнению: 4х + 40 = 7 х + 16, где х р. – стоимость одной книги. В ходе решения данного уравнения мы проделываем следующие выкладки: 7 х – 4 х = 40 – 16 => Зх = 24 => х = 8, которые вместе с рассуждениями, использовавшимися при составлении уравнения, приводят к следующему арифметическому способу решения задачи. Найдем: на сколько больше купили бы книг (7 – 4 = 3); на сколько меньше осталось бы денег, то есть на сколько больше денег израсходовали (40 – 16 = 24); сколько стоит одна книга (24: 3 = 8). Проделанные рассуждения сведем в таблицу 4. Таблица 4
Оформим решение задачи арифметическим методом: 1) 7 – 4 = 3 (кн.) – на столько книг купили бы больше; 2) 40 – 16 = 24 (р.) – на столько рублей заплатили бы больше; 3) 24: 3 = 8 (р.) – стоит одна книга. Ответ: одна книга стоит 8 р. Пример. Из пункта А в пункт В вышел пароход со скоростью 24 км/ч. Из этого же пункта А восемью часами раньше вышел буксир с баржами со скоростью 8 км/ч. Буксир пришел в пункт В на 16 ч. позже, чем пароход. Найдите расстояние между пунктами А и В.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 4270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.32.116 (0.22 с.) |
 4. Из указанных трех операций непосредственно вытекает составление уравнения как оформление словесной записи при помощи математических символов.
4. Из указанных трех операций непосредственно вытекает составление уравнения как оформление словесной записи при помощи математических символов.

 По условию задачи
По условию задачи 


 которое автомобиль проезжает пути АВ и ВС соответственно.
которое автомобиль проезжает пути АВ и ВС соответственно. .
.

 Преобразовав уравнения, имеем систему из трех уравнений с тремя неизвестными:
Преобразовав уравнения, имеем систему из трех уравнений с тремя неизвестными:
 или
или 
 это совместная производительность рабочих, поэтому время, за которое они выполнят всю работу, будет равно
это совместная производительность рабочих, поэтому время, за которое они выполнят всю работу, будет равно

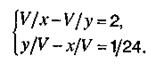






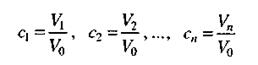








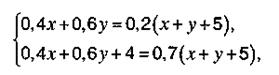
 сухого вещества. Эти же 1,8 т сухоговещества должны составить 20% массы свежескошенной травы, так как ее влажность по условию задачи равна 80%. Следовательно, если через х мы обозначим массу травы, которую надо накосить, чтобы получить 2 т сена, то получим пропорцию.
сухого вещества. Эти же 1,8 т сухоговещества должны составить 20% массы свежескошенной травы, так как ее влажность по условию задачи равна 80%. Следовательно, если через х мы обозначим массу травы, которую надо накосить, чтобы получить 2 т сена, то получим пропорцию.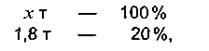


 Пользуясь таблицей 2, составим следующую систему уравнений:
Пользуясь таблицей 2, составим следующую систему уравнений: