
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение уравнения ПуассонаСодержание книги
Поиск на нашем сайте
ПУАССОНА УРАВНЕНИЕ
численные методы решения - методы, заменяющие исходную краевую задачу для уравнения Пуассона ∆u (x) ≡ системой из Nлинейных алгебраич. решение к-рой В зависимости от способа сравнения решений исходной задачи (1) и дискретной задачи (2) определяются такие важнейшие понятия, как погрешность численного метода и оценка погрешности (точности). Другими характеристиками численных методов служат алгебраич. свойства систем (2) (дискретных аналогов краевых задач), связанные с устойчивостью их решений (корректностью дискретных задач) и возможностью отыскания точных или приближенных решений (2) теми или иными прямыми или итерационными методами при выполнении соответствующей вычислительной работы и соответствующих требованиях на объем используемой памяти ЭВМ (см. Минимизация вычислительной работы).
Важность численного решения краевых задач для П. у. определяется не только тем, что эти задачи часто возникают в разнообразных областях науки и техники, но и тем, что они нередко служат и средством решения более общих краевых задач как для уравнений и систем уравнений эллиптич. типа, так и различных нестационарных систем. Основными численными методами для решения рассматриваемых краевых задач являются проекционные методы и разностные методы.
12. Численное решение обыкновенных дифференциальных уравнений. Метод последовательных приближений Пикара. Этот метод позволяет получить решение дифференциального уравнения (1) в виде функции, представленной аналитически. Пусть в условиях теоремы существования требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части Очевидно, решение интегрального уравнения (5) будет удовлетворять дифференциальному уравнению (1) и начальному условию (2).
Действительно, при x=x0получим:. вместе с тем интегральное уравнение (5) позволяет применить метод последовательных приближений. Положим y=y0 и получим из (5) первое
приближение:. Интеграл в правой части содержит только переменную х; после нахождения этого интеграла будет получено аналитическое выражение приближения y1(x) как функции переменной х. Заменим теперь в уравнении (5) у найденным значением y1(x) и получим второе
приближение: и т.д. В общем случае итерационная формула имеет вид:
Циклическое применение формулы (6) дает последовательность функций
Так как функция f непрерывна в области G, то она ограниченна в некоторой области G??? G, содержащей точку (x0,y0), то есть
Применяя к уравнению (6) в условиях теоремы существования принцип сжимающих отображений, нетрудно показать, что последовательность (7) сходится. Ее предел является решением интегрального уравнения (1) с начальными условиями (2). Это озночает, что k- ый член последовательности (7) является приближением к точному решению уравнения (1) с определенной степенью точности. Оценка погрешности k -го приближения дается формулой:
Где М - константа Липшица (4), N - верхняя грань модуля функции f из неравенства (8), а величина d для определения окрестности
Сеток метод собирательное название группы приближённых методов решения дифференциальных, интегральных и интегро-дифференциальных уравнений. Применительно к дифференциальным уравнениям с частными производными термин «С. м.» используется в качестве синонима терминов «метод конечных разностей» и «разностный метод». С, м. — один из наиболее распространённых приближённых методов решения задач, связанных с дифференциальными уравнениями. Широкое применение С. м. объясняется его большой универсальностью и сравнительной простотой реализации на ЭВМ. Суть С. м. состоит в следующем: область непрерывного изменения аргументов, в которой ищется решение уравнения, дополненного, если необходимо, краевыми и начальными условиями, заменяется дискретным множеством точек (узлов), называемым сеткой; вместо функций непрерывного аргумента рассматриваются функции дискретного аргумента, определяемые в узлах сетки и называемые сеточными функциями; производные, входящие в уравнение, краевые и начальные условия, аппроксимируются разностными отношениями; интегралы аппроксимируются квадратурными формулами; при этом исходное уравнение (задача) заменяется системой (линейных, если исходная задача была линейной) алгебраических уравнений (системой сеточных уравнений, а применительно к дифференциальным уравнениям — разностной схемой). Если полученная таким образом система сеточных уравнений разрешима, по крайней мере, на достаточно мелкой сетке, т. е. сетке с густым расположением узлов, и её решение при неограниченном измельчании сетки приближается (сходится) к решению исходного уравнения (задачи), то полученное на любой фиксированной сетке решение и принимается за приближённое решение исходного уравнения (задачи).
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 (1)
(1)
 ≡(
≡( ,
,  позволяет построить нек-рую аппроксимацию Pn Un для решения исходной задачи,N→∞.
позволяет построить нек-рую аппроксимацию Pn Un для решения исходной задачи,N→∞. уравнения (1) от x0 до х:
уравнения (1) от x0 до х:  ,
,
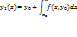

 (6).
(6). (7).
(7). (8).
(8).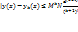 , (9)
, (9) вычисляется по формуле
вычисляется по формуле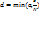 (10)
(10) 


