
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение обыкновенных дифференциальных уравнений. Метод Рунге-Кутта.
Семейство явных методов Рунге-Кутты р -го порядка записывается в виде совокупности формул:
Параметры
6. Многочлен Ньютона интерполяционный. Пусть в точках х 0, х 1, …, х n+1 значения функции у = f (x) равны соответственно у 0 = f (x 0), y 1 = f (x 1), …, y n+1 = f (x n+1). Построим интерполяционный многочлен Ньютона с помощью метода неопределенных коэффициентов. Для этого запишем искомый многочлен в виде Последовательно подставляя в формулу (1) вместо х данные значения х 0, х 1,..., х n+1, получим для нахождения неопределенных коэффициентов b 0, b 1,..., b n«треугольную» систему уравнений Полученную систему удобно решать: из первого её уравнения находим свободный член искомого многочлена b 0; подставив его во второе уравнение, находим коэффициент b 1 при первой степени х в искомом многочлене:
Численное решение обыкновенных дифференциальных уравнений. Метод Коши Задача Коши для одного обыкновенного дифференциального уравнения. Рассматривается задача Коши для одного дифференциального уравнения первого порядка разрешенного относительно производной
Требуется найти решение на отрезке Введем разностную сетку на отрезке Точки
Приближенное решение задачи Коши (4.1) будем искать численно в виде сеточной функции. Для оценки погрешности приближенного численного решения будем рассматривать это решение как элемент N+1- мерного линейного векторного пространства с какой либо нормой. В качестве погрешности решения принимается норма элемента этого пространства
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.252 (0.006 с.) |

 (1)
(1)

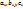 подбираются так, чтобы значение
подбираются так, чтобы значение  , рассчитанное по соотношению (1) совпадало со значением разложения в точке
, рассчитанное по соотношению (1) совпадало со значением разложения в точке  точного решения в ряд Тейлора с погрешностью O(
точного решения в ряд Тейлора с погрешностью O(
 (при подстановке в равенство (1) вместо х числа х 0 в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х 0), обратившийся в нуль; при подстановке х = х 1 обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х 1) и т.д.).
(при подстановке в равенство (1) вместо х числа х 0 в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х 0), обратившийся в нуль; при подстановке х = х 1 обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х 1) и т.д.).
 (4.1)
(4.1)
 где
где 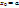 .
.
 - называются узлами разностной сетки, расстояния между узлами – шагом разностной сетки (h), а совокупность значений какой либо величины заданных в узлах сетки называется сеточной функцией
- называются узлами разностной сетки, расстояния между узлами – шагом разностной сетки (h), а совокупность значений какой либо величины заданных в узлах сетки называется сеточной функцией 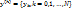
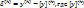 - точное решение задачи (1) в узлах расчетной сетки. Таким образом
- точное решение задачи (1) в узлах расчетной сетки. Таким образом 



