
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии устойчивости Гурвица.
Теорема 21.3. Для асимптотической устойчивости системы с характеристическим полиномом (21.1) необходимо и достаточно, чтобы при
Правило составления матрицы 1. По главной диагонали выписываем коэффициенты характеристического полинома с 2. Заполняем строки так, чтобы чередовались строки с нечетными и четными индексами элементов. 3. Элементы с индексами большими Частные случаи:
меньше нельзя (смотри критерий Столье) Вывод: смотри теорему 21.1.
Таким образом, условия критерия Гурвица для систем Критические случаи:
Поскольку 1.
2.
3.
§22. Частотный критерий устойчивости Найквиста.
Лемма 22.1. Пусть
Критерий Найквиста для АФХ.
Позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы.
передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Рассмотрим вспомогательную функцию
Пример: Первый случай:
(по предположению)
(требуется)
Это означает, что годограф вектора
Теорема 22.1. Если передаточная функция разомкнутой системы имеет только левые корни, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении
не охватывает Пусть Рассмотрим возможный вид АФХ при разных
Пусть
Легко увидеть, что замкнутая система асимптотически устойчива, но теряет устойчивость, как при увеличении, так и при уменьшении контурного коэффициента Замечание: формулировка теоремы 22.1. сохраняет свою силу, если передаточная функция разомкнутой системы кроме левых имеет также один нулевой полюс (смотри дальше). Второй случай:
Этот случай принципиально не отличается от первого, но имеет особенности изображения частотных функций. Пусть
Пусть
АФХ разомкнутой системы не охватывает точку
Пусть
При
Теорема 22.2. Если передаточная функция разомкнутой системы кроме левых полюсов имеет один или несколько нулевых, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы дополненное при Третий случай: имеется
Теорема 22.3. Если передаточная функция разомкнутой системы имеет Замечание: если при
Теорема 22.4. Если передаточная функция разомкнутой системы имеет Замечание: В первом случае подпадает под эту формулировку
Критерий Найквиста для ЛЧХ.
Теорема 22.5. Если передаточная функция разомкнутой системы имеет Замечание 1: дополнение при Замечание 2: если Замечание 3: если при Замечание 4: следующий случай непосредственно не подпадает под формулировку теоремы 22.5, но может быть рассмотрен исходя из основной теоремы 22.4. если во всем диапазоне частот ЛАХ разомкнутой системы лежит ниже оси абсцисс, то при Доказательство теоремы 22.5 следует из двух фактов: 1.
2.
Следствие: (упрощенная формулировка для случая устойчивости разомкнутой системы с монотонной ЛАХ). Если в передаточной функции разомкнутой системы есть только левые полюсы и возможно еще один нулевой, а ЛАХ разомкнутой системы монотонна, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы на частоте среза ЛФХ разомкнутой системы проходила выше уровня
Качество САУ.
Качество САУ – степень соответствия системы к двум требованиям: 1. Регулируемая переменная 2. Реакция Оба требования можно объединить в требованиях ошибки
Для количественной характеристики качества динамики вводятся показатели качества САУ. Они делятся на:
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.150 (0.045 с.) |
 были положительны все главные диагональные миноры матрицы Гурвица
были положительны все главные диагональные миноры матрицы Гурвица  :
:
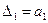



 :
: по
по  (
( коэффициенты при
коэффициенты при  );
); и меньшими нуля заменяются на ноль.
и меньшими нуля заменяются на ноль.











 порядка таковы, что все коэффициенты
порядка таковы, что все коэффициенты  и выполняется
и выполняется  .
.
 то различают три случая:
то различают три случая:
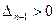 (и остальные
(и остальные 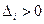 ) апериодическая граница устойчивости.
) апериодическая граница устойчивости.
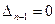 (и остальные
(и остальные  полином в степени
полином в степени  правых и
правых и  левых корней, тогда изменение аргумента функции
левых корней, тогда изменение аргумента функции  при увеличении
при увеличении 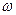 определяется выражением
определяется выражением  (22.1)
(22.1)
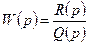

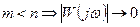 при
при 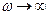 т.е. АФХ разомкнутой системы стремится к началу координат.
т.е. АФХ разомкнутой системы стремится к началу координат.


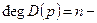 характеристический полином замкнутой системы
характеристический полином замкнутой системы характеристический полином разомкнутой системы
характеристический полином разомкнутой системы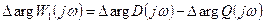 (22.2)
(22.2)
 (разомкнутая система асимптотически устойчива);
(разомкнутая система асимптотически устойчива);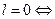 лемма
лемма 
 лемма
лемма 

 при увеличении
при увеличении  не охватывает точку
не охватывает точку  .
.

 не охватывала точку
не охватывала точку  равнялась нулю:
равнялась нулю:  .
.
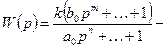 Гурвицев полином (корни только левые).
Гурвицев полином (корни только левые).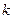 .
. АФХ разомкнутой системы не охватывает
АФХ разомкнутой системы не охватывает  следовательно, замкнутая система устойчива.
следовательно, замкнутая система устойчива. Замкнутая система находится на границе устойчивого колебательного типа.
Замкнутая система находится на границе устойчивого колебательного типа. АФХ разомкнутой системы охватывает
АФХ разомкнутой системы охватывает  следовательно, замкнутая система неустойчива.
следовательно, замкнутая система неустойчива.

 полюс кратности
полюс кратности  .
. , тогда
, тогда 

 скачек аргумента
скачек аргумента  (поворот вектора по часовой стрелке – дуга бесконечного радиуса).
(поворот вектора по часовой стрелке – дуга бесконечного радиуса). АФХ разомкнутой системы охватывает точку
АФХ разомкнутой системы охватывает точку  дополнение при
дополнение при  , тогда
, тогда 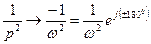

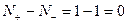 следовательно, замкнутая система асимптотически устойчива.
следовательно, замкнутая система асимптотически устойчива.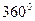 . В то время как при
. В то время как при  (если не рассматривать отрицательных частот).
(если не рассматривать отрицательных частот). .
.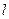 правых полюсов, а остальные левые.
правых полюсов, а остальные левые.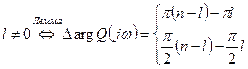
 , следовательно,
, следовательно,  , т.е. вектор
, т.е. вектор 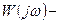 вокруг точки
вокруг точки  раз для
раз для 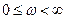 ).
). раз при
раз при  , или что тоже самое
, или что тоже самое 
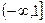 , то это соответствует
, то это соответствует  перехода через этот луч, т.е.
перехода через этот луч, т.е.  .
.
 , дугой бесконечного радиуса в направлении против часовой стрелки
, дугой бесконечного радиуса в направлении против часовой стрелки  .
. равнялась
равнялась 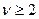 дополнение обязательно. Если
дополнение обязательно. Если  дополнение обязательно независимо от
дополнение обязательно независимо от  следует
следует  , т.е. АФХ разомкнутой системы не может охватить точку
, т.е. АФХ разомкнутой системы не может охватить точку  Для точек перехода АФХ через луч
Для точек перехода АФХ через луч 
 , а
, а  .
. Переходу АФХ сверху вниз соответствует переход ЛФХ через
Переходу АФХ сверху вниз соответствует переход ЛФХ через  должна как можно лучше воспроизводить закон изменения
должна как можно лучше воспроизводить закон изменения 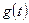 .
. : мгновенные значения
: мгновенные значения 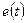 должны быть как можно меньше, а
должны быть как можно меньше, а 


