
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статические свойства сау. (проблема точности). Основные принципы ау. Общая структура сау.Содержание книги
Поиск на нашем сайте
Основные понятия.
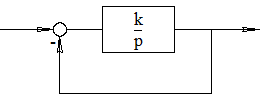
Управление – воздействие на некоторый объект (объект управления), влияющее на протекающие в нём процессы и осуществляемое для достижения определенной цели – цели управления. Пример 1.1. Система автоматического управления скоростью вращения.
Uос – Обратная связь
Элементы схемы: ЗУ – Задающее устройство Uз – Задающее напряжение Р(УУ) – Регулятор (управляющее устройство) Uу – Управляющее напряжение УПУ – Усилительно-преобразовательное устройство Иу – Исполнительное устройство Ис – Напряжение сети Двиг – Двигатель ТГ – Тахогенератор
ЦУ – цель управления состоит в том, чтобы обеспечить с определенной точностью изменения управляемой переменной Идеальная ЦУ:
где Однако ЦУ (1.1) недостижима из-за:
2.
Вариант практической цели управления.
где Представим систему в следующем виде:
Uз, Uc, Мн – выходные воздействия. Они делятся на две принципиально различающиеся группы:
Общая структура САУ.
ЗУ – обычно на схемах не изображают. УС – необходимо для составления И – измеритель Часто УС и Р(УУ) совмещается водном устройстве.
Классификация САУ.
1. разомкнутые; 2. замкнутые (с обратной связью);
3. комбинированные (сочетают регулирование по отклонению с регулированием по внешнему воздействию).
1. системы автоматического регулирования (САР) – цель управления состоит в возможно более точном воспроизведении регулируемой переменной САР в зависимости от вида функции
Для всех трех типов САР цель управления может быть сформулирована одинаково в терминах ошибки регулирования: она должна быть как можно меньше по абсолютному значению и как можно быстрее затухать; пример ЦУ:
2. (не для запоминания) САУ других типов (обычно более сложные), например:
1. линейные и нелинейные САУ; в линейной системе все элементы описываются линейными уравнениями (дифференциальными, алгебраическими и др.); уравнение линейно, если для него выполняется принцип суперпозиции, предполагающий наличие свойств однородности и аддитивности, как по входным воздействиям, так и по начальным условиям. Как линейные, так и нелинейные системы бывают: · стационарные и нестационарные (уравнения с постоянными или зависящими от времени коэффициентами); · с сосредоточенными и распределенными параметрами (дифференциальные уравнения обыкновенные и с частными производными);
· системы с запаздыванием (уравнения с запаздывающим аргументом); · дискретные системы (разностные уравнения); · статические и динамические системы (алгебраические или дифференциальные, возможно вместе с алгебраическими, уравнения). IV. По характеру преобразования переменных в элементах системы:
1. непрерывные системы – в них в каждом 2. релейные системы – в них хотя бы в одном элементе при непрерывном изменении 3. дискретные системы – в их элементах значение выхода дискретные системы делятся на: · импульсные (в них имеется квантование по времени) и · цифровые, или системы с ЭВМ (квантование по времени и по уровню).
1. Детерминированные и стохастические САУ (определенные и случайные процессы).
VI. По числу входных (задающих) и выходных (управляемых) переменных:
1. одномерные (с одним входом и одним выходом) и многомерные(со многими входами и (или) выходами) системы; 2. односвязные системы (каждая компонента вектора выходов Физический смысл ЧПФ.
ЧПФ – частотная передаточная функция:
Неминимально-фазовые звенья
Звено называется неминимально-фазовым если его передаточная функция не имеет ни нулей, ни полюсов в правой полуплоскости. Пример 9.2. Минимально-фазовое звено
полюс:
Неминимально-фазовое звено
полюс:
Таким образом, два звена (НМФ и МФ) могут иметь одинаковые АЧХ (ЛАХ), но различные ФЧХ (ЛФХ), при этом МФ на каждой данной частоте имеет наименьшее по абсолютной величине значения ФЧХ. Важнейшее свойство МФ систем – однозначность связи АЧХ и ФЧХ. Поэтому по ЛАХ МФ системы всегда можно восстановить её передаточную функцию.
Теорема Мейсена.
Назначение: Определение передаточной функции между двумя переменными структурной схемы или графа. Является альтернативой методу структурных преобразований. Терминология: Путь – это направленная последовательность звеньев, в которой ни одна переменная не встречается ни одного раза. Контур – это замкнутый путь. Передача пути (контура) – произведение передач всех звеньев встречающихся на этом пути (в этом контуре), с учетом знаков в сумматорах. Теорема 14.1. Передача связывающая входную переменную где
Замечание: Говорят, что контур не касается другого или пути, если он не имеет с ним общих переменных.
Критерий Найквиста для АФХ.
Позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы.
передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Рассмотрим вспомогательную функцию
Пример: Первый случай:
(по предположению)
(требуется)
Это означает, что годограф вектора
Теорема 22.1. Если передаточная функция разомкнутой системы имеет только левые корни, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении
не охватывает Пусть Рассмотрим возможный вид АФХ при разных
Пусть
Легко увидеть, что замкнутая система асимптотически устойчива, но теряет устойчивость, как при увеличении, так и при уменьшении контурного коэффициента Замечание: формулировка теоремы 22.1. сохраняет свою силу, если передаточная функция разомкнутой системы кроме левых имеет также один нулевой полюс (смотри дальше). Второй случай:
Этот случай принципиально не отличается от первого, но имеет особенности изображения частотных функций.
Пусть
Пусть
АФХ разомкнутой системы не охватывает точку
Пусть
При Теорема 22.2. Если передаточная функция разомкнутой системы кроме левых полюсов имеет один или несколько нулевых, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы дополненное при Третий случай: имеется
Теорема 22.3. Если передаточная функция разомкнутой системы имеет Замечание: если при
Теорема 22.4. Если передаточная функция разомкнутой системы имеет Замечание: В первом случае подпадает под эту формулировку
Критерий Найквиста для ЛЧХ.
Теорема 22.5. Если передаточная функция разомкнутой системы имеет Замечание 1: дополнение при
Замечание 2: если Замечание 3: если при Замечание 4: следующий случай непосредственно не подпадает под формулировку теоремы 22.5, но может быть рассмотрен исходя из основной теоремы 22.4. если во всем диапазоне частот ЛАХ разомкнутой системы лежит ниже оси абсцисс, то при Доказательство теоремы 22.5 следует из двух фактов: 1.
2.
Следствие: (упрощенная формулировка для случая устойчивости разомкнутой системы с монотонной ЛАХ). Если в передаточной функции разомкнутой системы есть только левые полюсы и возможно еще один нулевой, а ЛАХ разомкнутой системы монотонна, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы на частоте среза ЛФХ разомкнутой системы проходила выше уровня
Качество САУ.
Качество САУ – степень соответствия системы к двум требованиям: 1. Регулируемая переменная 2. Реакция Оба требования можно объединить в требованиях ошибки
Для количественной характеристики качества динамики вводятся показатели качества САУ. Они делятся на:
Частотные оценки качества.
Оценка вида (23.1) справедлива и для произвольной ЛАХ если:
Вообще
Запасы устойчивости.
· По модулю · По фазе
Чем меньше
На значения запасов устойчивости наибольшее влияние оказывает коэффициент наклона ЛАХ в окрестности
Для первой системы
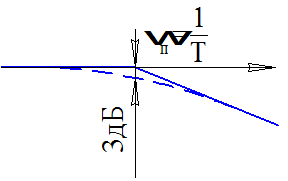
Показатель колебательности.
Чем больше М, тем больше Хорошая система имеет Средняя система
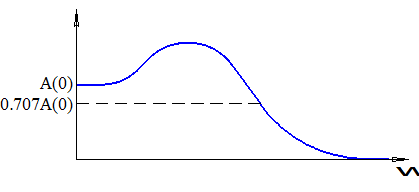
Полоса пропускания
Является мерой быстродействия системы.
В целом для САУ
Корневые оценки качества.
1. Степень устойчивости Рассмотрим систему третьего порядка: Пусть
2. Колебательность 3. Диаграмма Вышнеградского. Для системы третьего порядка позволяет оценить качественную картину расположения корней характеристического полинома и значения Пусть
Вводим новую комплексную переменную
где
По критерию Гурвица асимптотическая устойчивость эквивалентна Уравнения границы устойчивости:
Точка
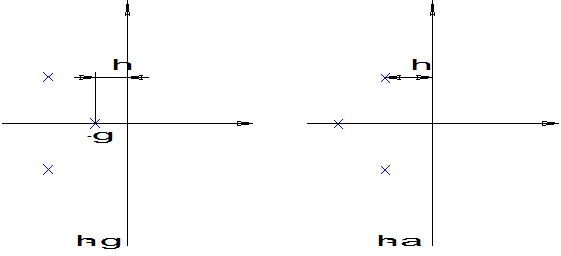
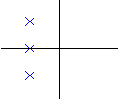
Стандартные полиномы Полиномы со стандартной картиной расположения корней на плоскости.
Корни этих полиномов располагаются на окружности радиусом
Существуют и другие стандартные полиномы:
таким образом
Точность САУ.
Степень близости
Установившаяся ошибка. Она возникает как от
Перерисуем схему так, чтобы выходом стала ошибка
Если Если
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.94.168 (0.012 с.) |

 Мн – Момент нагрузки
Мн – Момент нагрузки управляемая (регулируемая) переменная.
управляемая (регулируемая) переменная. задающее воздействие.
задающее воздействие. в соответствии с требуемым законом
в соответствии с требуемым законом  задаваемым с помощью напряжения
задаваемым с помощью напряжения  .
. для всех
для всех  (1.1)
(1.1)
 изменилась скачком, то
изменилась скачком, то 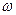 не может измениться (требуется бесконечное значение).
не может измениться (требуется бесконечное значение).
 линейно, то для изменения
линейно, то для изменения 
 . В данной схеме без обратной связи отсутствие контроля за фактическим значением
. В данной схеме без обратной связи отсутствие контроля за фактическим значением  для всех
для всех  (1.2)
(1.2) заданы.
заданы.
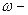 управляемая переменная является выходной величиной (суммой реакций на все выходные величины).
управляемая переменная является выходной величиной (суммой реакций на все выходные величины).
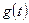 и
и  .
. . На выходе УС
. На выходе УС  .
. ;
;
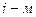 звене при непрерывном изменении входной переменной
звене при непрерывном изменении входной переменной 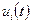 выходная
выходная  изменяется также непрерывно;
изменяется также непрерывно; ; при этом выход дискретного элемента имеет вид последовательности импульсов;
; при этом выход дискретного элемента имеет вид последовательности импульсов; зависит только от одной, соответствующей ей, компоненты вектора входов
зависит только от одной, соответствующей ей, компоненты вектора входов  ) и многосвязные системы (хотя бы одна из компонент
) и многосвязные системы (хотя бы одна из компонент  характеризует поведение динамической системы в установившемся режиме при гармоническом входном воздействии и представляет собой комплексную функцию, модуль которой на каждой данной частоте есть отношение амплитуд выходной и входной гармоник, а аргумент равен фазовому сдвигу всех гармоник относительно входной (смотри теорему (7.1).
характеризует поведение динамической системы в установившемся режиме при гармоническом входном воздействии и представляет собой комплексную функцию, модуль которой на каждой данной частоте есть отношение амплитуд выходной и входной гармоник, а аргумент равен фазовому сдвигу всех гармоник относительно входной (смотри теорему (7.1).
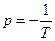









 с выходной
с выходной  определяется формулой:
определяется формулой: 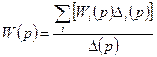 ,
, передача
передача 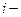 го пути от
го пути от 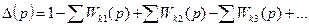
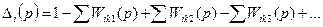
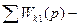 сумма передач всех контуров
сумма передач всех контуров сумма произведений передач, не касающихся друг друга контуров, взятых по два.
сумма произведений передач, не касающихся друг друга контуров, взятых по два.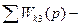 сумма произведений передач, не касающихся друг друга контуров, взятых по три.
сумма произведений передач, не касающихся друг друга контуров, взятых по три. 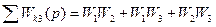 .
.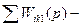 сумма передач контуров, не касающихся
сумма передач контуров, не касающихся 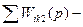 сумма произведений передач, не касающихся
сумма произведений передач, не касающихся  сумма произведений передач, не касающихся
сумма произведений передач, не касающихся 
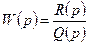

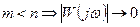 при
при 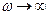 т.е. АФХ разомкнутой системы стремится к началу координат.
т.е. АФХ разомкнутой системы стремится к началу координат.


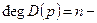 характеристический полином замкнутой системы
характеристический полином замкнутой системы характеристический полином разомкнутой системы
характеристический полином разомкнутой системы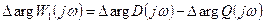 (22.2)
(22.2)
 (разомкнутая система асимптотически устойчива);
(разомкнутая система асимптотически устойчива);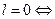 лемма
лемма 
 лемма
лемма 

 при увеличении
при увеличении  не охватывает точку
не охватывает точку  .
.

 не охватывала точку
не охватывала точку  равнялась нулю:
равнялась нулю:  .
.
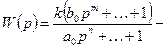 Гурвицев полином (корни только левые).
Гурвицев полином (корни только левые).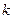 .
. АФХ разомкнутой системы не охватывает
АФХ разомкнутой системы не охватывает  следовательно, замкнутая система устойчива.
следовательно, замкнутая система устойчива. Замкнутая система находится на границе устойчивого колебательного типа.
Замкнутая система находится на границе устойчивого колебательного типа. АФХ разомкнутой системы охватывает
АФХ разомкнутой системы охватывает  следовательно, замкнутая система неустойчива.
следовательно, замкнутая система неустойчива.

 полюс кратности
полюс кратности  .
. , тогда
, тогда 

 скачек аргумента
скачек аргумента  (поворот вектора по часовой стрелке – дуга бесконечного радиуса).
(поворот вектора по часовой стрелке – дуга бесконечного радиуса). АФХ разомкнутой системы охватывает точку
АФХ разомкнутой системы охватывает точку  дополнение при
дополнение при  , тогда
, тогда 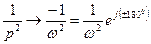

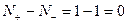 следовательно, замкнутая система асимптотически устойчива.
следовательно, замкнутая система асимптотически устойчива. . В то время как при
. В то время как при  (если не рассматривать отрицательных частот).
(если не рассматривать отрицательных частот). .
. правых полюсов, а остальные левые.
правых полюсов, а остальные левые.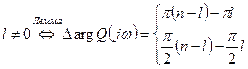
 , следовательно,
, следовательно,  , т.е. вектор
, т.е. вектор 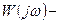 вокруг точки
вокруг точки  раз для
раз для 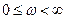 ).
). раз при
раз при  , или что тоже самое
, или что тоже самое 
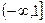 , то это соответствует
, то это соответствует  перехода через этот луч, т.е.
перехода через этот луч, т.е.  .
.
 , дугой бесконечного радиуса в направлении против часовой стрелки
, дугой бесконечного радиуса в направлении против часовой стрелки  .
. равнялась
равнялась 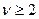 дополнение обязательно. Если
дополнение обязательно. Если  дополнение обязательно независимо от
дополнение обязательно независимо от  следует
следует  , т.е. АФХ разомкнутой системы не может охватить точку
, т.е. АФХ разомкнутой системы не может охватить точку  Для точек перехода АФХ через луч
Для точек перехода АФХ через луч 
 , а
, а  .
. Переходу АФХ сверху вниз соответствует переход ЛФХ через
Переходу АФХ сверху вниз соответствует переход ЛФХ через  : мгновенные значения
: мгновенные значения 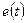 должны быть как можно меньше, а
должны быть как можно меньше, а 


 (23.1)
(23.1)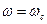 составляет
составляет  ;
; ;
; связано не только с
связано не только с  , но и со степенью демпфирования системы
, но и со степенью демпфирования системы  .
.



 , тем больше запас по модулю. Если бы точка б совместилась с точкой
, тем больше запас по модулю. Если бы точка б совместилась с точкой 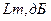

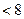

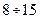






 .
.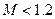 ;
; ;
;

 примерно, так же как и с
примерно, так же как и с  . Расстояние от мнимой оси до ближайшего к ней корня характеристического полинома замкнутой системы или пары сопряженных корней. Является мерой быстродействия системы, поскольку та составляющая свободного решения, которая определяется ближайшим к мнимой оси корнем (парой корней) затухает наиболее медленней и следовательно определяет время переходного процесса.
. Расстояние от мнимой оси до ближайшего к ней корня характеристического полинома замкнутой системы или пары сопряженных корней. Является мерой быстродействия системы, поскольку та составляющая свободного решения, которая определяется ближайшим к мнимой оси корнем (парой корней) затухает наиболее медленней и следовательно определяет время переходного процесса.
 доминирует
доминирует  доминирует
доминирует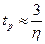 (23.2)
(23.2) 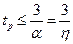 (23.3)
(23.3) . Отношение модулей мнимой части и вещественной частей к мнимой оси пары комплексно сопряженных корней
. Отношение модулей мнимой части и вещественной частей к мнимой оси пары комплексно сопряженных корней  . Практически требуют, чтобы все комплексные корни лежали в секторе с заданным углом
. Практически требуют, чтобы все комплексные корни лежали в секторе с заданным углом 

 , делим все на
, делим все на 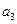
 (23.4)
(23.4)
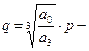 подставляем в (23.4)
подставляем в (23.4) (23.5)
(23.5)

 .
.



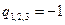



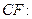

 .
.



 на одинаковом условном расстоянии друг от друга симметрично оси вещественных.
на одинаковом условном расстоянии друг от друга симметрично оси вещественных.



 (23.6)
(23.6)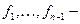 коэффициенты определяющие вид переходной характеристики системы с передаточной функцией
коэффициенты определяющие вид переходной характеристики системы с передаточной функцией  (23.7)
(23.7)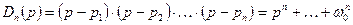


 к
к  (24.1)
(24.1) . Поэтому
. Поэтому  (24.2)
(24.2)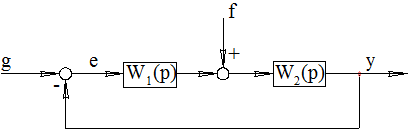

 это
это  , либо
, либо  .
. , то
, то  ;
;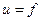 , то
, то  ;
; полиномы с единичными свободными членами.
полиномы с единичными свободными членами.



