
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор системы счисления для представления числовой информацииСодержание книги
Поиск на нашем сайте
Информация во внешнем по отношению к ЭВМ мире представляется в непрерывном или дискретном виде. Внутри ЭВМ информация всегда представляется в виде чисел, записанных в той или иной системе счисления. Если же речь идет о текстовой информации, то она обычно кодируется также с помощью чисел. Вопрос о выборе системы счисления для цифрового автомата – один из важнейших вопросов проектирования, как алгоритмов функционирования отдельных устройств, так и расчета технических характеристик этого автомата. Система счисления – совокупность приемов и правил для записи чисел цифровыми знаками. Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры от 0 до 9. Существует большое множество способов записи чисел цифровыми знаками. Любая предназначенная для практического применения система счисления должна обеспечивать: - возможность представления любого числа в рассматриваемом диапазоне величин; - единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина); - простоту оперирования числами. Все системы представления чисел делят на позиционные и непозиционные. Самый простой способ записи чисел может быть описан выражением:
где По этому принципу построены непозиционные системы счисления. Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе. Примером непозиционной системы счисления является система с одним символом – палочкой. Для изображения числа в этой системе нужно записать количество палочек равное данному числу. Позиционная система счисления – система, в которой значение цифры определяется ее положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней два десятка, а левая две сотни. Любая позиционная система счисления характеризуется основанием. Основание позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе. В общем случае позиционные системы счисления можно построить по следующему правилу:
где Если предположить, что
где На практике используют сокращенную запись числа:
В табл. 1.1 приведены эквиваленты десятичных цифр в различных системах счисления. Таблица 1.1
В ЭВМ используют позиционные системы счисления. Вес разряда
где i – номер разряда при отсчете справа налево. Если разряд имеет вес Длина числа (ДЧ) количество позиций (или разрядов) в записи числа. В техническом аспекте длина сила интерпретируется как длина разрядной сетки (ДРС). Для разных систем счисления характерна разная длина разрядной сетки, необходимая для записи одного и того же числа. Например, Если длина разрядной сетки задана, то это ограничивает максимальное (минимальное) по абсолютному значению число, которое может быть записано. Пусть длина разрядной сетки n. Тогда Диапазон представления (ДП) чисел в заданной системе счисления – интервал числовой оси, заключенный между максимальным и минимальным числами, представленными длиной разрядной сетки:
Правильный выбор системы счисления – важный практический вопрос, от правильного решения которого зависят такие технические характеристики проектируемой ЭВМ как скорость вычислений, объем памяти, сложность алгоритмов выполнения арифметических операций. При выборе системы счисления для ЭВМ необходимо учитывать следующее: - основание системы счисления определяет количество устойчивых состояний, которые должен иметь функциональный элемент, выбранный для изображения разрядов числа; - длина числа существенно зависит от основания системы счисления; - система счисления должна обеспечить простые алгоритмы выполнения арифметических и логических операций. Подавляющее большинство компонентов электронных схем, применяемых для построения вычислительных машин – двухпозиционные. С этой точки зрения для ЭВМ наиболее подходит двоичная система счисления. Для оценки рациональности использования той или иной системы счисления используется показатель экономичности системы – произведение основания системы счисления на длину разрядной сетки, выбранную для записи числа в этой системе:
где q – основание системы счисления; N – количество разрядов. Если принять, что каждый разряд числа представлен не одним элементом с q устойчивыми состояниями, а q элементами, каждый из которых имеет одно устойчивое состояние, то показатель экономичности укажет условное количество оборудования, которое необходимо затратить на представление чисел в этой системе. Максимальное число, которое можно изобразить в системе с основанием q:
Отсюда можно найти требуемую длину разрядной сетки:
Тогда для любой системы счисления Предположим, что величина q является непрерывной величиной. Тогда величину C можно рассматривать как функцию от величины q. Это допущение позволяет использовать для сравнения любой системы счисления с двоичной относительный показатель экономичности:
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

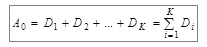 ,
, - запись числа А в системе счисления D;
- запись числа А в системе счисления D;  - символы системы, образующие базу
- символы системы, образующие базу  .
. ,
, - основание системы счисления;
- основание системы счисления;  - запись числа А в системе счисления с основанием
- запись числа А в системе счисления с основанием  ;
;  - цифра (символ) системы счисления с основанием
- цифра (символ) системы счисления с основанием  , то для позиционной системы счисления справедливо равенство
, то для позиционной системы счисления справедливо равенство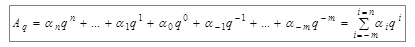 ,
, - произвольное число, записанное в системе счисления с основанием q; m – количество целых и дробных разрядов.
- произвольное число, записанное в системе счисления с основанием q; m – количество целых и дробных разрядов. .
. числа в позиционной системе счисления выражается соотношением:
числа в позиционной системе счисления выражается соотношением: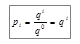 ,
, , то следующий старший разряд будет иметь вес
, то следующий старший разряд будет иметь вес  , а следующий младший разряд – вес
, а следующий младший разряд – вес  . Такая взаимосвязь разрядов приводит к необходимости передачи информации между ними.
. Такая взаимосвязь разрядов приводит к необходимости передачи информации между ними. . Из этого примера видно, чем меньше основание системы, тем больше длина числа.
. Из этого примера видно, чем меньше основание системы, тем больше длина числа. ;
;  .
. .
. ,
, .
. .
. .
. .
.


