
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление отрицательных чиселСодержание книги Поиск на нашем сайте
Для машинного представления отрицательных чисел используют коды прямой, обратный и дополнительный. Машинное изображение прямого кода числа Правила преобразования чисел в прямой код можно сформулировать так:
где G – величина, равная весу старшего разряда сетки (для дробей G = 1, а для целых Машинное изображение обратного кода числа Правила преобразования в обратный код можно сформулировать следующим образом:
где B – величина наибольшего числа без знака, размещающегося в n-разрядной сетке (для дробей При проектировании цифровых автоматов необходимо учитывать неоднозначность изображения нуля в обратном коде: +0 изображается 0,00…0, -0 изображается 1,11…1. Дополнительный код числа A, представляемого в n-разрядной сетке, определяется как
где C – величина, равная весу разряда, следующая за старшим разрядом используемой разрядной сетки (для дробей Дополнительный код является математическим дополнением основанию системы счисления:
где Если рассматривать обратные и дополнительные коды числа, то можно увидеть, что
Это соотношение используют для получения дополнительного кода отрицательного числа следующим образом: сначала инвертируется цифровая часть исходного числа, в результате получается его обратный код; затем прибавляется единица в младший разряд цифровой части и тем самым получается дополнительный код этого числа. Формы представления чисел В ЭВМ применяют две формы представления чисел: с фиксированной точкой и с плавающей точкой. Эти формы называют также соответственно естественной и нормальной (полулогарифмической).
При представлении чисел с фиксированной точкой положение точки фиксируется в определенном месте относительно разрядов числа. Обычно подразумевается, что точка находится перед старшим цифровым разрядом или после младшего. В первом случае могут быть представлены только числа, которые по модулю меньше 1, во втором – только целые числа. На рис. 1.1 показаны примеры форматов данных для представления чисел с фиксированной запятой. Для представления числа со знаком для кода знака выделяется «знаковый» разряд (обычно крайний слева). В этом разряде 0 соответствует плюсу, 1 – минусу. На рис. 1.1, а показан формат для чисел с точкой, фиксированной перед старшим разрядом. В этом формате могут быть представлены правильные дроби с точностью до
Используется два варианта представления целых чисел: со знаком и без знака (рис. 1.1, б и рис. 1.1, в). Если точка фиксируется справа от младшего разряда, то в n – разрядной сетке целых чисел со знаком можно представлять нуль, положительные и отрицательные целые двоичные числа. Дополнительный код позволяет использовать числа в диапазоне
Рисунок 1.1. Представление чисел в форме с фиксированной запятой При представлении целых чисел без знака все разряды разрядной сетки отводятся под модуль числа. Представление чисел в форме с плавающей точкой в общем случае имеет вид
где Мантисса и порядок представляются в системе счисления с основанием q. Порядок p, который может быть положительным или отрицательным целым числом, определяет положение точки в числе. На рис. 1.2 показаны примеры форматов данных для чисел с плавающей точкой. Формат должен содержать знаковые части и поля для мантиссы и порядка. Выделяются специальные разряды для знака числа (мантиссы) и знака порядка (рис. 1.2, а). Кодирование знаков остается таким же, как было и с фиксированной запятой.
Рисунок 1.2. Представление чисел в формате с плавающей точкой Выполнение арифметических операций над числами с плавающей точкой требуют помимо выполнения операций над мантиссами определенных операций над порядками. Для упрощения операций над порядками их сводят к действию над целыми положительными числами (числами без знаков), применяя для представления порядков смещенный код (представление чисел с плавающей точкой со смещенным порядком).
В случае представления числа с плавающей запятой со смещенным порядком к его порядку p прибавляется целое число - Смещенный порядок Такое представление чисел неоднозначно. Для определенности вводятся некоторые ограничения. Наиболее распространено и удобно для представления в ЭВМ ограничение вида
Такая форма представления чисел называется нормализованной. В этом случае абсолютное значение мантиссы лежит в пределах от В процессе вычислений может получиться ненормализованное число. В этом случае машина автоматически нормализует его. Пусть r старших разрядов мантиссы равно 0. Тогда нормализация заключается в сдвиге мантиссы на r разрядов влево и уменьшении порядка на r единиц, при этом в младшие r разрядов мантиссы записываются нули.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.007 с.) |

 -
- 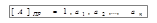 . Отсюда следует, что в прямом коде все цифровые разряды отрицательного числа остаются неизменными, а в знаковой части записывается единица. Например, если
. Отсюда следует, что в прямом коде все цифровые разряды отрицательного числа остаются неизменными, а в знаковой части записывается единица. Например, если  , то
, то  . Положительное число в прямом коде не меняет своего изображения. Например, если
. Положительное число в прямом коде не меняет своего изображения. Например, если  , то
, то 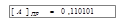 .
. ,
, ).
).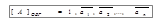 . Отсюда следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т.е. все нули заменяются на единицы, а все единицы – на нули. Например, если
. Отсюда следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т.е. все нули заменяются на единицы, а все единицы – на нули. Например, если  .
.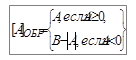 ,
, , а для целых -
, а для целых -  ).
). ,
, , а для целых чисел
, а для целых чисел  ). Например, число
). Например, число 
 .
. - абсолютное значение числа A.
- абсолютное значение числа A.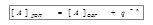 .
. . Если для представления чисел используется прямой код, то они могут принимать значения в диапазоне
. Если для представления чисел используется прямой код, то они могут принимать значения в диапазоне .
. .
.
 ,
, - мантисса числа А; p - порядок числа А, q – основание системы счисления.
- мантисса числа А; p - порядок числа А, q – основание системы счисления.
 , где k – число двоичных разрядов, используемых для модуля порядка.
, где k – число двоичных разрядов, используемых для модуля порядка. всегда положителен (рис.1.2, б).
всегда положителен (рис.1.2, б). .
. до
до  , где n – количество разрядов для изображения мантиссы без знака.
, где n – количество разрядов для изображения мантиссы без знака.


