
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление числовой информации в цифровых автоматахСодержание книги Поиск на нашем сайте
ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ В ЦИФРОВЫХ АВТОМАТАХ Представление отрицательных чисел Для машинного представления отрицательных чисел используют коды прямой, обратный и дополнительный. Машинное изображение прямого кода числа Правила преобразования чисел в прямой код можно сформулировать так:
где G – величина, равная весу старшего разряда сетки (для дробей G = 1, а для целых Машинное изображение обратного кода числа Правила преобразования в обратный код можно сформулировать следующим образом:
где B – величина наибольшего числа без знака, размещающегося в n-разрядной сетке (для дробей При проектировании цифровых автоматов необходимо учитывать неоднозначность изображения нуля в обратном коде: +0 изображается 0,00…0, -0 изображается 1,11…1. Дополнительный код числа A, представляемого в n-разрядной сетке, определяется как
где C – величина, равная весу разряда, следующая за старшим разрядом используемой разрядной сетки (для дробей Дополнительный код является математическим дополнением основанию системы счисления:
где Если рассматривать обратные и дополнительные коды числа, то можно увидеть, что
Это соотношение используют для получения дополнительного кода отрицательного числа следующим образом: сначала инвертируется цифровая часть исходного числа, в результате получается его обратный код; затем прибавляется единица в младший разряд цифровой части и тем самым получается дополнительный код этого числа. Формы представления чисел В ЭВМ применяют две формы представления чисел: с фиксированной точкой и с плавающей точкой. Эти формы называют также соответственно естественной и нормальной (полулогарифмической).
При представлении чисел с фиксированной точкой положение точки фиксируется в определенном месте относительно разрядов числа. Обычно подразумевается, что точка находится перед старшим цифровым разрядом или после младшего. В первом случае могут быть представлены только числа, которые по модулю меньше 1, во втором – только целые числа. На рис. 1.1 показаны примеры форматов данных для представления чисел с фиксированной запятой. Для представления числа со знаком для кода знака выделяется «знаковый» разряд (обычно крайний слева). В этом разряде 0 соответствует плюсу, 1 – минусу. На рис. 1.1, а показан формат для чисел с точкой, фиксированной перед старшим разрядом. В этом формате могут быть представлены правильные дроби с точностью до
Используется два варианта представления целых чисел: со знаком и без знака (рис. 1.1, б и рис. 1.1, в). Если точка фиксируется справа от младшего разряда, то в n – разрядной сетке целых чисел со знаком можно представлять нуль, положительные и отрицательные целые двоичные числа. Дополнительный код позволяет использовать числа в диапазоне
Рисунок 1.1. Представление чисел в форме с фиксированной запятой При представлении целых чисел без знака все разряды разрядной сетки отводятся под модуль числа. Представление чисел в форме с плавающей точкой в общем случае имеет вид
где Мантисса и порядок представляются в системе счисления с основанием q. Порядок p, который может быть положительным или отрицательным целым числом, определяет положение точки в числе. На рис. 1.2 показаны примеры форматов данных для чисел с плавающей точкой. Формат должен содержать знаковые части и поля для мантиссы и порядка. Выделяются специальные разряды для знака числа (мантиссы) и знака порядка (рис. 1.2, а). Кодирование знаков остается таким же, как было и с фиксированной запятой.
Рисунок 1.2. Представление чисел в формате с плавающей точкой Выполнение арифметических операций над числами с плавающей точкой требуют помимо выполнения операций над мантиссами определенных операций над порядками. Для упрощения операций над порядками их сводят к действию над целыми положительными числами (числами без знаков), применяя для представления порядков смещенный код (представление чисел с плавающей точкой со смещенным порядком).
В случае представления числа с плавающей запятой со смещенным порядком к его порядку p прибавляется целое число - Смещенный порядок Такое представление чисел неоднозначно. Для определенности вводятся некоторые ограничения. Наиболее распространено и удобно для представления в ЭВМ ограничение вида
Такая форма представления чисел называется нормализованной. В этом случае абсолютное значение мантиссы лежит в пределах от В процессе вычислений может получиться ненормализованное число. В этом случае машина автоматически нормализует его. Пусть r старших разрядов мантиссы равно 0. Тогда нормализация заключается в сдвиге мантиссы на r разрядов влево и уменьшении порядка на r единиц, при этом в младшие r разрядов мантиссы записываются нули.
Умножение двоичных чисел Цифровые автоматы Основные понятия Общая теория автоматов разбивается на две больших части - абстрактную теорию автоматов и структурную теорию автоматов. Различие между ними заключается в том, что в абстрактной теории изучается поведение автомата, отвлекаясь как от структуры самого автомата (способа построения, схемной реализации), так и его входных и выходных данных. Абстрактная теория изучает лишь те переходы, которые претерпевает автомат под воздействием входных сигналов, и те выходные сигналы, которые он при этом выдает. Абстрактная теория близка к теории алгоритмов, является ее дальнейшей детализацией. В структурной теории автоматов рассматриваются, прежде всего, структуры, как самого автомата, так и его входных и выходных сигналов. В структурной теории изучаются способы построения автоматов из элементарных автоматов, способы кодирования входных и выходных сигналов элементарными сигналами и т.п. Поэтому термин автомат, как правило, используется в двух аспектах. С одной стороны автомат – устройство, выполняющее некоторые функции без непосредственного участия человека. В этом смысле ЭВМ – это автомат, так как после загрузки программы и исходных данных ЭВМ решает заданную задачу без участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов. В этом аспекте автомат представляется как «черный ящик», имеющий конечное число входов и выходов и некоторое множество внутренних состояний Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов – конечные множества. В практике часто используется понятие цифрового автомата, под которым понимают устройство, предназначенное для преобразования цифровой информации.
Входные сигналы в цифровых автоматах представляются в виде конечного множества мгновенных сигналов. Такое допущение упрощает рассмотрение процессов, происходящих в автоматах, так как все события (состояния) должны относиться к фиксированному моменту времени t. Автомат под действием входных сигналов принимает состояния в соответствии с набором значений входных сигналов и выдает сигналы, зависящие от внутреннего состояния автомата либо от внутреннего состояния и входных сигналов. Условно принимается, что число выходных сигналов Если выходной сигнал Пусть имеется цифровой автомат с одним входом (рис. 5.1)
Рис.5.1. Абстрактный автомат с одним входом и одним выходом Математической моделью цифрового автомата является абстрактный автомат, заданный совокупностью шести объектов: 1) конечное множество X входных сигналов (входной алфавит автомата)
2) конечное множество Y выходных сигналов (выходной алфавит автомата)
3) произвольное множество Q состояний автомата
4) начальное состояние автомата
5) функция 6) функция В начальный момент времени Понятие состояния автомата используется для описания систем, выходы которых зависят не только от входных сигналов в данный момент времени, но и от сигналов, которые поступили на входы системы ранее. Состояние автомата позволяет устранить время, как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов. Работу абстрактного автомата следует рассматривать применительно к конкретным интервалам времени, так как каждому интервалу дискретности t может соответствовать свой выходной сигнал
Время для цифрового автомата имеет также важное значение. Для решения задач анализа и синтеза цифровых автоматов обычно вводится автоматное время. Функционирование автомата рассматривается через дискретные интервалы времени конечной продолжительности (интервал дискретности). Существует два способа задания автоматного времени, по которым цифровые автоматы делят на два класса: синхронные и асинхронные. В синхронных автоматах моменты времени, в которых фиксируются изменения состояний автомата, задаются специальным устройством – генератором синхросигналов, выдающим импульсы через равные промежутки времени (постоянный интервал дискретности). В асинхронных автоматах моменты перехода автомата из одного состояния в другое заранее не определены и зависят от каких-то событий. В таких автоматах интервал дискретности является переменным. Автоматы классифицируются по двум основным признакам. 1. Объем памяти. Памятью автомата называют число его состояний. Автоматы Поста (или Тьюринга) являются бесконечными автоматами, т.к. имеют неограниченную память на ленте. Конечными автоматами являются отдельные части ЭВМ или вся машина. 2. Механизм случайного выбора. В детерминированных автоматах поведение и структура автомата в каждый момент времени однозначно определены текущей входной информацией и состоянием автомата. В вероятностных автоматах они зависят от случайного выбора. В теории автоматов наиболее полно описаны синхронные автоматы. В зависимости от способа определения выходного сигнала в синхронных автоматах существует две возможности: 1) выходной сигнал 2) выходной сигнал Следовательно, закон функционирования автомата может быть задан следующим образом: для автоматов первого рода системой уравнений
(5.1)
для автоматов второго рода системой уравнений
(5.2)
Автоматы первого рода с функцией выходов (5.1) называются автоматами Мили 1 рода, а автоматы второго рода с функцией выходов (5.2) – автоматами Мили 2 рода. Отличие системы уравнений (5.1) и (5.2) состоит в том, что выходное состояние Между моделями Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой и обратно. Совмещенная модель автомата (С-автомат). Абстрактный С-автомат – математическая модель дискретного устройства, для которого заданы следующие параметры:
Абстрактный С-автомат можно представить в виде устройства с одним входом, на который поступают сигналы входного алфавита X, и двумя выходами, на которых появляются сигналы из выходных алфавитов Y и U (рис. 5.2).
Рисунок 5.2. Совмещенная модель автомата с одним входом и двумя выходами Отличие С-автомата от моделей Мили и Мура состоит в том, он одновременно реализует две функции выходов
Выходной сигнал ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ В ЦИФРОВЫХ АВТОМАТАХ
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.014 с.) |

 -
- 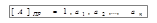 . Отсюда следует, что в прямом коде все цифровые разряды отрицательного числа остаются неизменными, а в знаковой части записывается единица. Например, если
. Отсюда следует, что в прямом коде все цифровые разряды отрицательного числа остаются неизменными, а в знаковой части записывается единица. Например, если  , то
, то  . Положительное число в прямом коде не меняет своего изображения. Например, если
. Положительное число в прямом коде не меняет своего изображения. Например, если  , то
, то 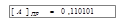 .
. ,
, ).
).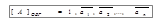 . Отсюда следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т.е. все нули заменяются на единицы, а все единицы – на нули. Например, если
. Отсюда следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т.е. все нули заменяются на единицы, а все единицы – на нули. Например, если  .
.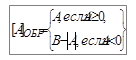 ,
, , а для целых -
, а для целых -  ).
). ,
, , а для целых чисел
, а для целых чисел  ). Например, число
). Например, число 
 .
. - абсолютное значение числа A.
- абсолютное значение числа A.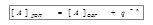 .
. . Если для представления чисел используется прямой код, то они могут принимать значения в диапазоне
. Если для представления чисел используется прямой код, то они могут принимать значения в диапазоне .
. .
.
 ,
, - мантисса числа А; p - порядок числа А, q – основание системы счисления.
- мантисса числа А; p - порядок числа А, q – основание системы счисления.
 , где k – число двоичных разрядов, используемых для модуля порядка.
, где k – число двоичных разрядов, используемых для модуля порядка. всегда положителен (рис.1.2, б).
всегда положителен (рис.1.2, б). .
. до
до  , где n – количество разрядов для изображения мантиссы без знака.
, где n – количество разрядов для изображения мантиссы без знака. , в которые он под воздействием входных сигналов переходит скачком. Конечно, это условие в реальности не выполняется, так как любой переходной процесс длится конечное время.
, в которые он под воздействием входных сигналов переходит скачком. Конечно, это условие в реальности не выполняется, так как любой переходной процесс длится конечное время. конечно. Для хранения внутреннего состояния автомат должен иметь память, таким образом, автомат является устройством с памятью, т.е. устройством последовательностного типа.
конечно. Для хранения внутреннего состояния автомат должен иметь память, таким образом, автомат является устройством с памятью, т.е. устройством последовательностного типа. или
или  и не зависит от входных сигналов, то цифровой автомат называется правильным.
и не зависит от входных сигналов, то цифровой автомат называется правильным.
 ;
; ;
; ;
; как элемент множества Q
как элемент множества Q ;
; (функция перехода автомата из одного состояния в другое);
(функция перехода автомата из одного состояния в другое); (функция выходов автомата).
(функция выходов автомата). автомат находится в состоянии
автомат находится в состоянии  и выдать соответствующий выходной сигнал
и выдать соответствующий выходной сигнал 
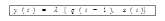 ,
,
 ,
, 
 - множество состояний;
- множество состояний; - входной алфавит;
- входной алфавит; - выходной алфавит типа 1;
- выходной алфавит типа 1;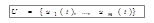 - выходной алфавит типа 2;
- выходной алфавит типа 2; - функция переходов, реализующая отображение
- функция переходов, реализующая отображение в Q.
в Q. - функция выходов, реализующая отображение
- функция выходов, реализующая отображение - функция выходов, реализующая отображение
- функция выходов, реализующая отображение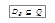 на U.
на U. - начальное состояние автомата.
- начальное состояние автомата.
 и
и  , каждая из которых характерна для этих моделей в отдельности. Этот автомат можно описать следующими уравнениями:
, каждая из которых характерна для этих моделей в отдельности. Этот автомат можно описать следующими уравнениями: ,
,  ,
,  (5.3)
(5.3) вырабатывается все время, пока автомат находится в состоянии
вырабатывается все время, пока автомат находится в состоянии  . Выходной сигнал
. Выходной сигнал  выдается во время действия входного сигнала
выдается во время действия входного сигнала  при нахождении автомата в состоянии
при нахождении автомата в состоянии 


