
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И 2 не подходят для оптимизации.Содержание книги Поиск на нашем сайте
без ограничения общности можно положить что матрица q – симметричная
Разложим функцию в ряд Тейлора (должно быть 3 члена). Чтобы найти линейный член квадратичной функции, надо взять grad.
Найдем матрицу Гесса (матрица вторых частных производных)
элемент матрицы Гесса является элементом функции Q. Функция экстремальна, если grad в данной точке равен 0,
Необходимое условие оптимальности: Если Если
Если имеем квадратичную функцию и матрица положительно определена, то линии уровня – эллипсы. Собственные значения определяют оси эллипсов.
Чтобы определить координаты точки локального минимума, нужно решить систему
Пусть f(x) – произвольная функция и надо найти точку локального минимума. Разложим функцию в ряд Тейлора в окрестности точки.
Пусть функция не квадратичная, эллипсы примерно отражают кривизну линий уровня и находятся в окрестности точки Находим точку минимума и рассматриваем эту точку как следующее приближение и т.д. Для нахождения точки минимума квадратичной функции (зависит от
Окончательно следующее приближение
(обобщение формулы минимизации одной переменной)
Выполнение метода останавливается когда Если f – хороша, то метод Ньютона подходит, если f – квадратичная функция, то метод Ньютона приводит к минимальной точке за 1 шаг, из любой точки.
Недостатки:
Все формулы безусловной минимизации можно записать в общую схему:
Допустим, требуется f(x)àmin;
а) выбор направления б) движение вдоль выбранного направления
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.205.161 (0.008 с.) |


 ;
;


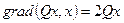 ;
; ; С = 0
; С = 0
 (все частные производные высших порядков равны 0).
(все частные производные высших порядков равны 0). - система.
- система.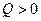 решение данной системы существует и оно единственное (совместная система).
решение данной системы существует и оно единственное (совместная система). решение данной системы существует и оно единственное, т.е. если Q знакоопределена, то существует решение и оно единственное.
решение данной системы существует и оно единственное, т.е. если Q знакоопределена, то существует решение и оно единственное.
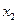
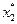


 .
.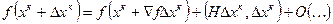
 . В окрестности точки
. В окрестности точки  )необходимо решить систему:
)необходимо решить систему:
 .
. - формула Ньютона
- формула Ньютона , т.е. когда
, т.е. когда  очень мало. Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.
очень мало. Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.
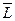



 - начальное приближение;
- начальное приближение; 






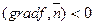 ;
;



