
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы одномерной оптимизации.Содержание книги Поиск на нашем сайте
Постановка: требуется оптимизировать х (формальная постановка)
Решение: найти х, при котором 2 варианта: - минимизировать – задача минимизации; - максимизировать – задача максимизации.
Рассмотрим случай минимизации
2 способа: - аналитический - численный
В аналитическом
Пусть функция определена в некоторой области S (
Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.
Аналитический способ нахождения локального минимума.
Численные методы.
а
Если из того что
Методы одномерного поиска.
Разобьем
искомый минимум
В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.
Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.
1) 2)
N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).
Метод золотого сечения.
Точки должны быть расположены на равном расстоянии.
число итераций растет как логарифм функции.
Одномерная оптимизация с использованием производных.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.245.158 (0.005 с.) |


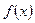 - функция одной переменной
- функция одной переменной 

 ), в случае одномерной оптимизации S – интервал
), в случае одномерной оптимизации S – интервал  :
: называется глобальным минимумом, если для
называется глобальным минимумом, если для 



 - необходимое условие точки локального минимума.
- необходимое условие точки локального минимума.


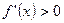


 Пусть функция
Пусть функция  , при этом существует такая точка
, при этом существует такая точка 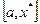 – монотонно убывает, а на
– монотонно убывает, а на  – монотонно возрастает, то функция унимодальная.
– монотонно возрастает, то функция унимодальная.
 следует, что
следует, что  , то функция называется монотонно возрастающей. Если из того что
, то функция называется монотонно возрастающей. Если из того что  следует, что
следует, что  , то функция называется монотонно убывающей.
, то функция называется монотонно убывающей. и вычислим значение функции в каждой точке.
и вычислим значение функции в каждой точке.


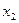







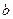

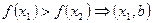
 - после выполнения n шагов сокращение исходного интервала
- после выполнения n шагов сокращение исходного интервала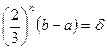
 - точность с которой надо найти решение задачи.
- точность с которой надо найти решение задачи.







 а b
а b
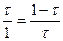 ;
;  ;
;  ;
; ;
; 
 а
а




 - величина сокращения на каждом шаге
- величина сокращения на каждом шаге
 . Пусть целевая функция дифференцируема
. Пусть целевая функция дифференцируема  .
.







